【信号与系统学习笔记 1】—— 信号的分类与信号的变换

这是《信号与系统》网上授课的第一次笔记，主要记录一下自己对信号分类以及信号变换的一些理解。

P.S：在《信号与系统》这门课中会经常用到 $Matlab$ 仿真，我会将全部仿真代码放到 $github$ 上

【戳这里！】我Blog 中关于《信号与系统》相关代码的 github地址

一、信号的分类

1.1 确定信号和不确定信号

这个概念其实很好理解：如果每一次发出的信号 $x$，它某一时刻的幅值每次都是固定的，那么这个信号就是确定信号。

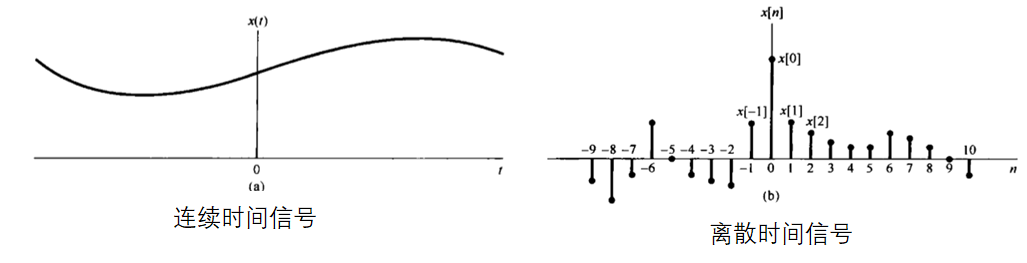
1.2 离散时间信号和连续时间信号

我们以后的课程约定：$x(t)$ 代表连续时间信号，用 $t$ 代表连续时间，圆括号括起来。注意：连续时间信号的自变量是连续的，幅值也是连续的。
$x[n]$ 代表离散时间信号，用 $n$ 代表离散时间（只能是整数！），方括号括起来。注意：离散时间信号的自变量是离散的，但是幅值是连续的。

1.3 周期信号和非周期信号

总所周知，对于连续时间信号 $y=sin(t)$ 显然是一个周期信号。但是离散时间下，$y[n]=sin(n)$ 还是不是周期信号呢?

答案是：不一定了！
下面通过一个例子说明：我们下面的第一幅图是 $t$ 从 [-10, 10] 的连续区间下的 $sin(t)$，第二幅图是 $n$ 在 [-10,10] 的区间下以 1秒为间隔的离散正弦信号：

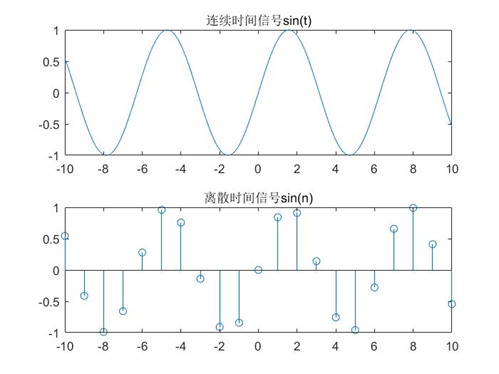
我们发现，按照这样的时间划分，$sin(n)$ 已经不再是周期信号了！

1.4 能量信号和功率信号

先来看看连续时间信号在一段时间 $t_1$~$t_2$ 内的能量：$$E={\int }_{t_1}^{t_2}|x(t){|}^{2}dt$$
那么很自然地，在这段时间内信号的平均功率就是：$$P=\frac{1}{t_2-t_1}E=\frac{1}{t_2-t_1}{\int }_{t_1}^{t_2}|x(t){|}^{2}dt$$

下面我们再看看离散时间信号在一段时间 $n_1$ ~ $n_2$ 的能量：$$E=\sum _{n=n_1}^{n_2}|x[n]{|}^2$$
对应地在这段时间内的平均功率为：$$P=\frac{1}{n_2-n_1+1}\sum _{n=n_1}^{n_2}|x[n]{|}^2$$
这里要特别注意：离散时间下 $n_1$ 与 $n_2$ 之间的间隔是 $n_2-n_1+1$ ！！

然而，这门课研究的，是信号的过去、现在和未来，因此，为了一般化，我们将时间取到无穷：
那么，对于连续时间信号而言，能量就可以表示成：$$E=\underset{t\to \infty }{\lim }{\int }_{-\frac{T}{2}}^{\frac{T}{2}}|x(t){|}^{2}dt$$
而功率就可以表示成：$$P=\underset{t\to \infty }{\lim }\frac{1}{2T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}|x(t){|}^{2}dt$$

对于离散时间信号而言，能量可以表示成：$$E=\underset{N\to \infty }{\lim }\sum _{n=-N}^N|x[n]{|}^2$$
功率可以表示成：$$P=\underset{N\to \infty }{\lim }\frac{1}{2N+1}\sum _{n=-N}^N|x[n]{|}^2$$
(同样要小心这里的时间间隔 $2N+1$）

下面整理给出无限时间内，连续时间信号和离散时间信号分别的能量和功率的表达式：

1. 连续时间信号
   $$\{\begin{array}{c}E={\lim }_{T\to \infty }{\int }_{-\frac{T}{2}}^{\frac{T}{2}}|x(t){|}^{2}dt\\ \\ P={\lim }_{T\to \infty }\frac{1}{2T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}|x(t){|}^{2}dt\end{array}$$

2. 离散时间信号
   $$\{\begin{array}{c}E={\lim }_{N\to \infty }{\sum }_{n=-N}^N|x[n]{|}^2\\ \\ P={\lim }_{N\to \infty }\frac{1}{2N+1}{\sum }_{n=-N}^N|x[n]{|}^2\end{array}$$

在我们得到了无限时间内，连续时间信号和离散时间信号分别的能量和功率的表达式之后，我们给出能量信号和功率信号的定义：

能量有限的，（功率为0）就是能量信号
功率有限的，（能量无穷）就是功率信号

我们看啊，假如这个信号是能量信号，也就说明 $E$ 是一个有限的数，而在无穷的时间里面积分还能得到有限的数，意味着这个信号总会有一个起点或者是终点，而不能无限延申下去

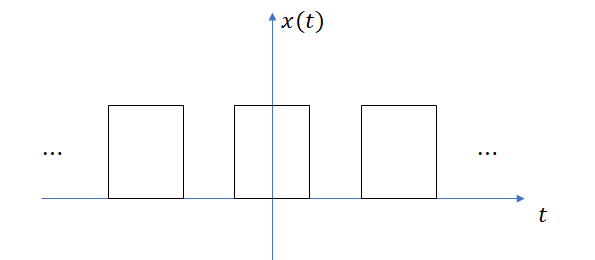
比如上面这样的周期信号，就不可能是能量信号了，因为它在 $t=\infty$ 的时候依然会有有幅值的地方，所以它的 E应该是无穷大。

也即是说：

1. 周期信号一定是功率信号
2. 能量信号一定不是周期信号

结合上面的讨论，我们从能量信号和功率信号的角度把周期信号和非周期信号分分类：
【1】首先对于周期信号，那必然是功率信号（因为在可以无限延拓下去，所以能量无穷，但是因为周期信号的幅度一定是有限的，所以它功率是一定的）

【2】对于非周期信号，我们可以分为3类：

1. 第一类：持续时间无限，幅度固定的非周期信号（功率信号）

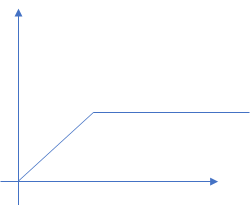
2. 只在一段有限时间内有幅度的信号，或者说持续时间有限（属于能量信号）

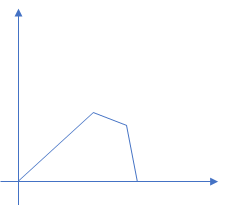
3. 随着时间的增长，幅度也一直增长：$t\to \infty ,x(t)\to \infty$ （非功非能信号）

二、信号的变换

2.1 信号的时移

这个好理解：$x(t)\to x(t-t_0)$，如果 $t_0$大于0，说明把信号向右平移。如果 $t_0$ 小于0，说明信号向左平移。下面用matlab 画一画：

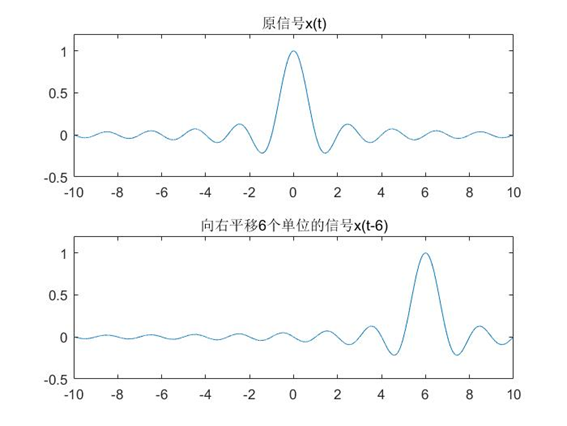
2.2 信号的反转变换

$x(t)$ 如果将他变成 $x(-t)$，就是相当于把 $x(t)$ 沿着纵轴镜像对称翻折得到。

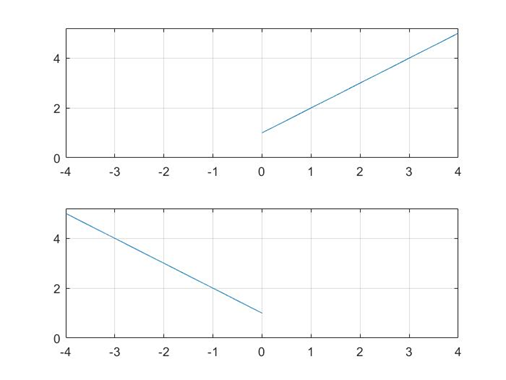
2.3 信号的尺度变换

如果对连续时间信号 $x(t)$ 做尺度变换 $x(at)$，有下面两种情况：

1. 如果 $a>1$ 相当于把信号压缩a倍（信号变瘦，高矮不变）
2. 如果 $0<a<1$,相当于把信号扩展$\frac{1}{a}$（信号变胖，高矮不变）

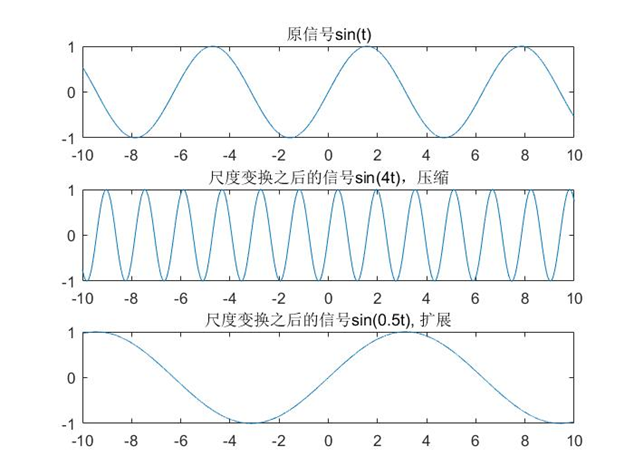
尺度变换建议的顺序：先平移$\to$ 再缩放，最后反转。关于缩放的技巧，我们可以先得到平移之后自变量的取值范围：$[i,j]$，接着看缩放系数 $a$，如果 $a>1$，那么自变量范围除以 $a$，$0<a<1$，那么就将范围增加 $\frac{1}{a}$ 倍。函数值的话自己看着现在自变量对应的原来函数的值写。

注意：自变量的基本变换都是针对 $t$ 来的，$x(-t+3)$ 其实是将 $x(-t)$ 向右移动3个单位！

---

【复习内容】：下面给出信号变换的妙招（防出错）：
一般对于信号的变换建议按照下面的顺序：先平移，然后再针对自变量 $t$ 或者 $n$ 做尺度变换

例如：为了获得 $x(\frac{3}{2}t+1)$，我们先将 $x(t)$ 向左平移1个单位，得到 $x(t+1)$，然后再针对自变量 $t$ 做尺度变换，得到 $x(\frac{3}{2}t+1)$

强调：尺度变换都是针对连续时间信号而言的，对于离散时间信号的“缩放”，其实只是抽取了其中的某个部分。另外，连续时间信号的尺度变换是可逆的，但是离散时间信号，你抽取了一部分，就不可能再换原回来了。