【波导】——理解群速度和相速度

概述

　对于接受阵的某个阵元来说，其空间位置固定，接收到的是声场时域信号。
　在理想波导中，我们假设声源是单频的，推导出了声场的表达式，是由可以传播的各号简正波叠加而成：
$$p(z,r;\omega )=\sum _{n=1}^N\sqrt{\frac{2\pi }{k_{rn}r}}{\phi }_n(k_{zn}{z}_0){\phi }_n(k_{zn}z)e^{-j{k}_{rn}r}$$
　其中${\phi }_n$是垂直方向上的模态函数，影响该垂直位置的柱面波的振幅。各号模态函数的分布如下图所示，n号简正波的模态函数有n-1个零点：
　

单频信号

我们取某一阵元的深度$z_h$，考虑第一号简正波和第二号简正波的区别，首先写出它们的表达式(依旧考虑单频声源)：
　$$p_1(r;t)=B_1{\phi }_1(k_{z1}{z}_0){\phi }_1(k_{z1}{z}_h)e^{j(\omega t-k_{r1}r)}$$$$p_2(r;t)=B_2{\phi }_2(k_{z2}{z}_0){\phi }_2(k_{z2}{z}_h)e^{j(\omega t-k_{r2}r)}$$
　可以发现，如果固定水平位置$r$，即在一个阵元上接收到的时域信号的频率是相同的，不同号简正波的差别在振幅和初相位；而固定时间$t$，即在某一时刻，不同号简正波在空间上的重复不一样(也就是水平波数)，当然振幅和初相位也不同。
　
　这里就可以引入相速度的概念，即同一相位的传播速度。对于固定深度的某一号简正波，其相位可以表示为$\omega t-k_{r}r$，故其相速度为：
　$$c_{pn}=\frac{w}{k_r}=\frac{c_0}{\sqrt{1-(\frac{k_{zn}}{k_0}{)}^2}}$$
　对应的也就是该深度处该号简正波的传播速度。所以如果是单频声源，那么不同号简正波可以通过不同的传播速度区分开来。

宽带信号

如果声源的频谱是存在一定的带宽的，根据傅里叶变换对，信号可以写成多个单频的简谐波叠加的形式，对于简谐波依旧可以用简正波理论去进行研究。
　$$p(t)=\frac{1}{2\pi }{\int }_{{\omega }_0}^{{\omega }_0+△\omega }p(\omega )e^{j\omega t}\mathrm{d}\omega$$
　所以声场是由不同号简正波叠加形成，而每一号简正波又是通过不同频率的简谐柱面波叠加而成，这里选取某一号简正波来进行研究，我们知道它是由不同频率的简谐柱面波叠加得到的，所以可以进行傅里叶分解。
　$$p_n(t,r)=\frac{1}{2\pi }{\int }_{{\omega }_0}^{{\omega }_0+△\omega }S(\omega )p_n(\omega )e^{j\omega t}\mathrm{d}\omega$$$$p_n(\omega )=\sqrt{\frac{2\pi }{k_{rn}r}}{\phi }_n(k_{zn}{z}_0){\phi }_n(k_{zn}{z}_h)e^{-j{k}_{rn}r}$$
　因为是同一号简正波，所以$k_{zn}$相同，$k_{rn}$随频率而变，而$S(\omega )$则是频谱密度，仅与频率有关，与简正波号数无关。不同频率的简谐波叠加会有拍现象，形成波包：
　
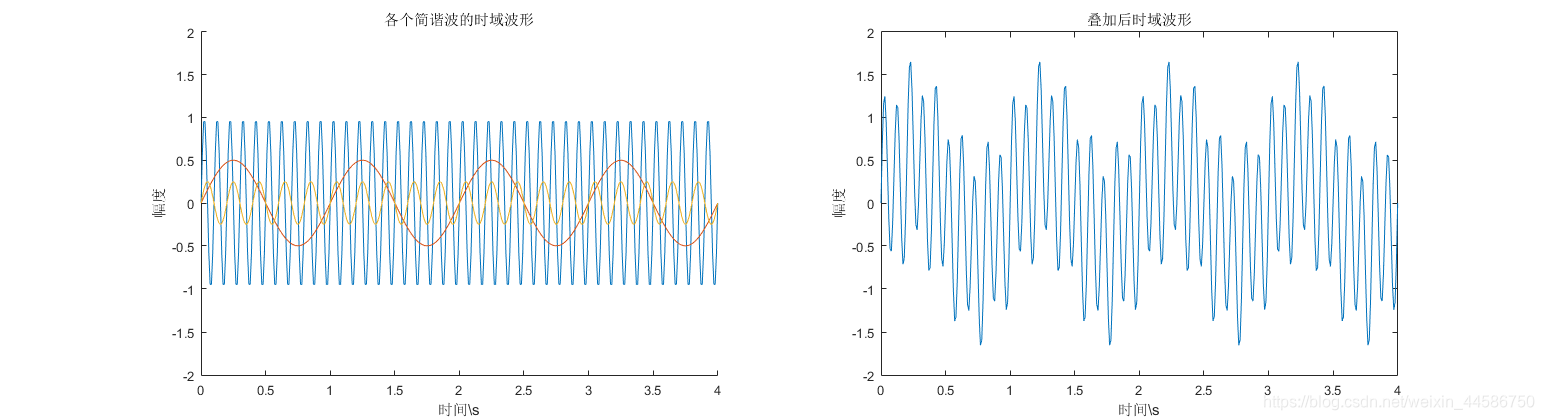
　对叠加信号进行分解，将$\omega (k_r)$在$k_{r0}$处泰勒展开$\omega (k_r)={\omega }_0+\frac{d\omega }{d{k}_{r0}}(k_r-k_{r0})$：
　$$f(t,r)=\int c(\omega )e^{j(\omega t-k_{r}r)}\mathrm{d}\omega$$$$f(t,r)=\int c(\omega )e^{j({\omega }_0+\frac{d\omega }{d{k}_r}(k_r-k_{r0}))t}{e}^{-j(k_{r0}+k_r-k_{r0})r}\mathrm{d}\omega$$$$f(t,r)=c({\omega }_0)e^{j({\omega }_{0}t-k_{r0}r)}\int e^{j(k_{r0}-k_r)(\frac{d\omega }{d{k}_r}t-r)}\mathrm{d}\omega$$$$\frac{d\omega }{d{k}_r}{|}_{k_r=k_{r0}}=const$$
　个人理解，上式是信号的频带在较窄的情况进行线性展开的近似，前一项是调制，后一项是波包。是对这一号简正波的近似。
　由此引出群速度的定义：
　$$c_{gn}=\frac{dw}{d{k}_r}=c_0\sqrt{1-(\frac{k_{zn}}{k_0}{)}^2}$$
　物理意义是该号简正波能量的传播速度，也可以理解为振幅的传播速度or波包的传播速度。相速度大于群速度，如果相位传过去了，但振幅没有传过去，能量还是没有传过去。

模间频散与模内频散

模间频散：不同号简正波的群速度不同，号数低的跑得快

模内频散：同一号简正波，频率高的跑得快(频率高的群速度大)
个人理解：
1.在推导群速度时用到了小区间内的泰勒展开，此时的角频率范围应该在$[{\omega }_0-△\omega ,{\omega }_0+△\omega ]$，其中$△\omega \ll {\omega }_0$，而200-300Hz的频率区间显然过大，故将其分成很多个小区间，在小区间中进行泰勒展开，形成波包+调制的一个信号，整体的时域信号就是这些频率小区间上信号的叠加，所以会有模间频散的现象，即高频率的信号跑得快。

2.而又因为号数高的简正波在同一频率区间中群速度变化率大，所以模间频散的现象更加明显。

PS：做了一下仿真，频率区间范围越大，模间频散越厉害，那么上述理解应该对的。