【业务】7. A/B测试

原文

基础

定义

A/B测试是一种随机测试（试验），将两个不同的东西（A、B）进行假设比较。
A/B测试(A/B Testing)，又称A/B实验（AB实验）、A/B试验（AB试验）、对照试验，双盲试验、正交试验。
A/B测试是数据驱动的重要手段。
A/B测试的核心步骤：假设、检验。
本质：对照试验
流程：假设、抽样、检验、结论
基础：试验设计、抽样理论、假设检验

伪A/B测试

统计学基础

小样本 & 大样本

大样本、小样本之间并不是以样本量大小来区分的。
大样本：在样本量n→∞的条件下所进行的统计推断、问题分析，称为大样本问题。
小样本：在样本量固定的条件下所进行的统计推断、问题分析，不管样本量多大，都称为小样本问题。
一般统计学中的n≥30为大样本，n<30为小样本只是一种经验说法。

正态分布

z分布

scipy.stats.norm.pdf(x)

t分布

scipy.stats.t.pdf(x,自由度)

卡方分布

scipy..stats.chi2.pdf(x,自由度)

中心极限定理

原假设、备择假设

统计学中，假设是关于总体的陈述，可分为原假设和备择假设。
原假设(null hypothesis,也称零假设、虚无假设，记为H0),即实验之前原有的假设。原假设的统计含义是：A、B的差异为零（无差异）。
备择假设(alternative hypothesis,也称对立假设，记为H1),即对立于原假设。备择假设的统计含义是：若否定原假设，则这个假设可备选择。
关键点：H0与H1是相互对立的。
A/B测试中的原假设是指AB组指标无显著差异；备择假设是指AB组指标有显著差异。

第Ι类错误、第ΙΙ类错误

1. 第I类错误(Type I error)
   定义：若H0实际为真时，犯拒绝H0的错误，称为第I类错误。
   统计符号：犯第I类错误的概率用α表示，也称α错误（α error)。
   A/B测试：实际上新策略没有效（无显著差异），但试验显示新策略有效（有显著差异）。
2. 第II类错误(Type II error)
   定义：若H0实际为不真时，犯接受H0的错误，称为第Ⅱ类错误。
   统计符号：犯第II类错误的概率用β表示，也称β错误(β error)。
   A/B测试：实际上新策略有效（有显著差异），但试验显示新策略没有效（无显著差异）。
   
   

显著性水平

p 值

定义1：p 值（probability value，p -value）在观测数据下拒绝原假设的最小显著性水平。
定义2：p 值是指拒绝原假设犯第 Ι 类错误的最小概率。
定义3：p 值代表观察到的随机因素产生的差异概率。
当p值很小时，几乎不可能在零假设正确时出现目前的观测数据，因而拒绝零假设。
若p值≤α,则在显著性水平α下拒绝原假设H0。
若p值>α,则在显著性水平α下接受原假设H0。

统计功效

统计功效（statistical power），不犯第ΙΙ类错误（1-β）的概率。
A/B实验中的统计功效：当AB两组差异真的存在时，能正确判断的概率。
应用中常把统计功效定义在80%（β<0.2)以上。

效应量

效应量（Effect Size,又称效应值)，提供了对效应大小的具体测量；
效应量的分类：差异类(difference-type)、相关类(correlation-type)、组重叠(group-overlap)
A/B测试中，效应量属于差异类，是指对照组与实验组之间的差异大小。
效应量的特征：不依赖样本量，不依赖测量尺度，效应量的正负号仅表示效应的方向，其绝对值才是实际的效应大小。

MDE、MDES

Minimum Detectable Effect (MDE) ，即最小检测效应，也称检验灵敏度。
Minimum Detectable Effect Size (MDES)，MDE 与 MDES 是等价，但 MDE 的使用更普遍。

A/B测试原理

试验设计（Design of Experiment，DOE）

利用数学和统计学的方法来设计试验方案，称为统计试验设计，简称试验设计。

试验误差

试验误差可分为：随机误差、系统误差、过失误差。

1. 随机误差(random error)
   定义：试验中一些不可控的因素的综合作用称为随机误差。
   特点：客观存在的、不可避免的。
   影响：同一条件下的两次试验会得到不同的输出。
   量化：一般地，我们假设随机误差服从正态分布N(0,σ²)，其中方差σ²用于衡量随机误差的大小。
2. 系统误差(systematic error)
   在试验中没有被选为因素的变量，有系统的偏差称为系统误差。
3. 过失误差(mistake error)
   试验人员粗心大意造成的误差。
   精心设计试验，可以减少系统误差，避免过失误差的干扰。
   所以，在科学试验前提下，我们忽略系统误差、过失误差。

试验设计的基本原则

试验设计的变量

试验中需考察的变量称为因素或因子。
在科学试验的前提下，影响试验只有：因素和随机。
因素：这些变量必须是可以控制的。
随机：随机是不可控的，会带来随机误差。
定义3：p值代表观察到的随机因素产生的差异概率。

试验设计的方法

1. 因子试验设计(Factorial Experimental Design)
   研究变动着的因素效应的试验方法。
   A/B测试用的是因子试验设计中的单因素试验方法。
   单因素试验：一个试验中只选择了一个要考虑的因素。
2. 正交试验设计(Orthogonal Experimental Design)
   研究与处理多因素的一种实验方法。
   从全面试验的组合中挑选出部分有代表的点进行试验，即所谓部分因子设计。

为什么A/B测试用的是单因素试验？因为多因素试验无法控制变量，无法控制即无法量化效果。

抽样理论

抽样的定义：抽样(Sampling)就是从研究总体中选取一部分代表性样本的方法。
抽样的方法

1. 简单随机抽样(simple random sampling),也称纯随机抽样
2. 系统抽样(systematic sampling),也称等距抽样
3. 分层抽样(stratified sampling),也称类型随机抽样
   工业界，A/B测试通常用的是分层抽样。

分层抽样的定义

将抽样单元按某种特征或某种规则划分为不同的层，然后从不同的层中独立、随机地抽取样本。从而保证样本的结构与总体的结构比较相近，从而提高估计的精度。
分层抽样的目的：控制偶然性的影响，而提高样本的代表性。
分层抽样的本质：在使系统误差得到控制的前提下，尽量缩小随机误差的影响，有利于改善估计的精度。
A/B测试使用用户画像来进行分层抽样，获得代表性样本。
通常，无用户画像，无A/B测试，无数据驱动。
用户画像用于召回、排序、测试阶段——无用户画像，无推荐系统。

确定样本量

例：

假设检验

假设检验（Hypothesis Testing）是用来判断样本与样本，样本与总体的差异是由抽样误差引起，还是由本质差别造成的统计推断方法。
假设检验的基本思想：小概率原理

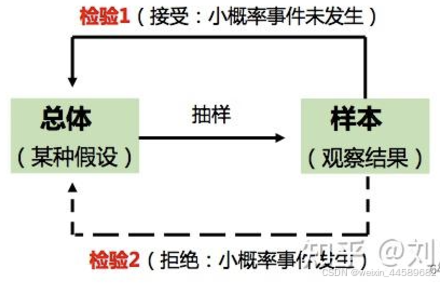
假设检验的步骤：

1. 先对总体的特征作出某种假设；
2. 然后通过抽样研究的统计推理；
3. 对此假设应该被拒绝还是接受作出判断。

z检验

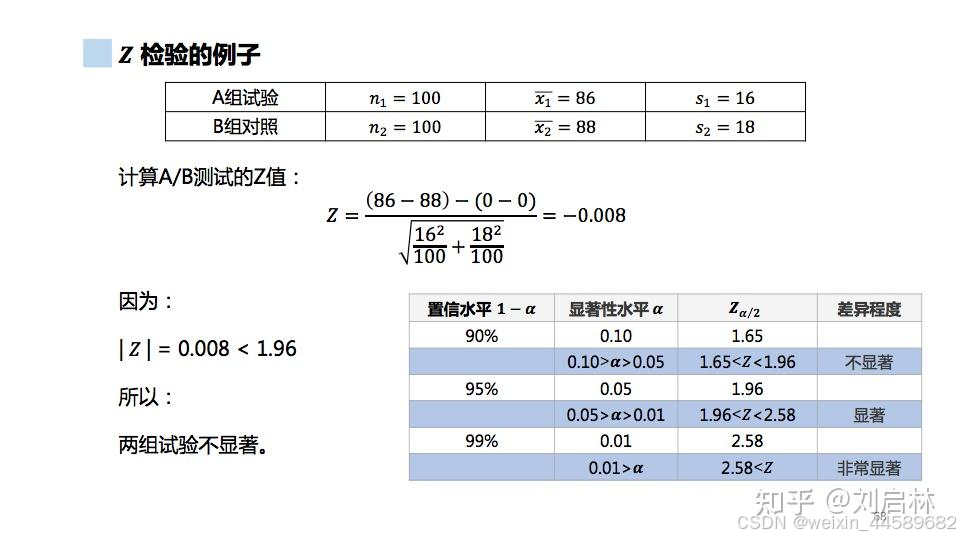
例：

t检验

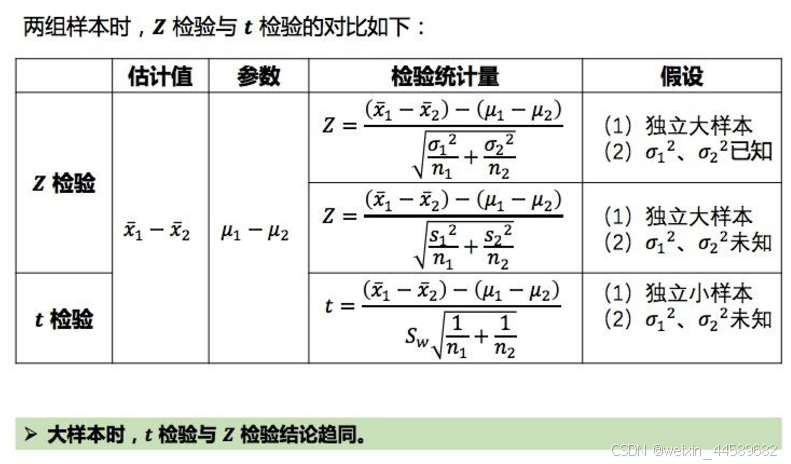
A/B测试通常样本量很大，用 Z 检验、t 检验都可以。
假设检验也有局限：

1. 假设检验更多地关注数据而非假设——置信区间
2. 显著性并不能反应业务价值的大小——效应量

卡方检验

例：

总结

案例

总结

A/B测试的本质

实验是科学研究的主流方法，其背后的指导思想是什么？

1. 实证主义：通过提出假设，然后在通过设计实验来验证这种假设是正确的。
2. 证伪主义：通过提出假设，然后在通过设计实验来验证这种假设是错误的。

A/B测试属于证伪主义，若试验没有统计显著性（差异），可以快速跳过继续下一个试验。

A/B测试的本质是对照试验。
A/B测试的本质的本质是证伪。
在A/B测试中，若试验没有统计显著性（差异），可以快速跳过继续下一个试验。

A/B测试的价值

数据化驱动决策：快速迭代模型、算法、策略、设计、流程。
降低风险：先小流量测试验证，再上线。
科学验证想法：根据数理统计学，降低人为的主观因素

A/B测试不适用

1. 变量多（调整多）：A/B测试适用于1个变量调整的对比实验。
2. 产品不成熟（用户极少）：初创公司，产品还没验证的时候。
3. 缺乏统计思维：指导思想错了，行为是盲目的，对产品伤害更大。

A/B测试的经验

1. 直接复制别人的经验，常常没有效果：用户群体不同、场景不同、产品不同、…
2. 注意心理学对A/B测试的影响：框架效应、实证性偏差、代表性启发、
3. 围绕北极星指标进行优化试验：试验的优先级，A/B测试的落脚点最终还是商业价值。