【HMM】隐马尔可夫/EM算法—数学公式黑板推导

目录

HMM概念和参数

Evaluate估计问题

求参问题-EM算法

EM算法公式推导

解码问题

---

HMM概念和参数

概率图模型：1到T时刻的状态呈现时间序列特性，通过T时刻的状态q，对应得出该时刻的观测值y。

三个参数：qt-1 -> qt 转移概率集合为A；qt -> yt 发射概率集合为B；q1的概率为π。

两个假设：1、齐次Markov：qt只与qt-1相关；2、观察独立：yt只与yt-1相关。

三个问题：1、已知参数λ={A,B,π}，求y的条件概率，即预估观测值y；2、通过数据学习参数λ；3、已知y和λ，解码最大概率Q序列。

Evaluate估计问题

计算观测变量Y，将状态变量Q放入，并对联合概率在Q上积分(离散积分=求和)；

利用齐次Markov假设：P(qt | q1:t-1,λ) = P(qt | qt-1,λ)；

每一个q都有N个取值，所以最后P(Y | λ) 是O(N^T)。！困难

计算P(Y | λ) 方法之forward algorithm： 

设αt = P(y1:t,qt | λ)，q取N个值概率的和即为P(Y | λ)；

探索αt+1和αt的迭代关系，再次利用两个假设（图中箭头）。

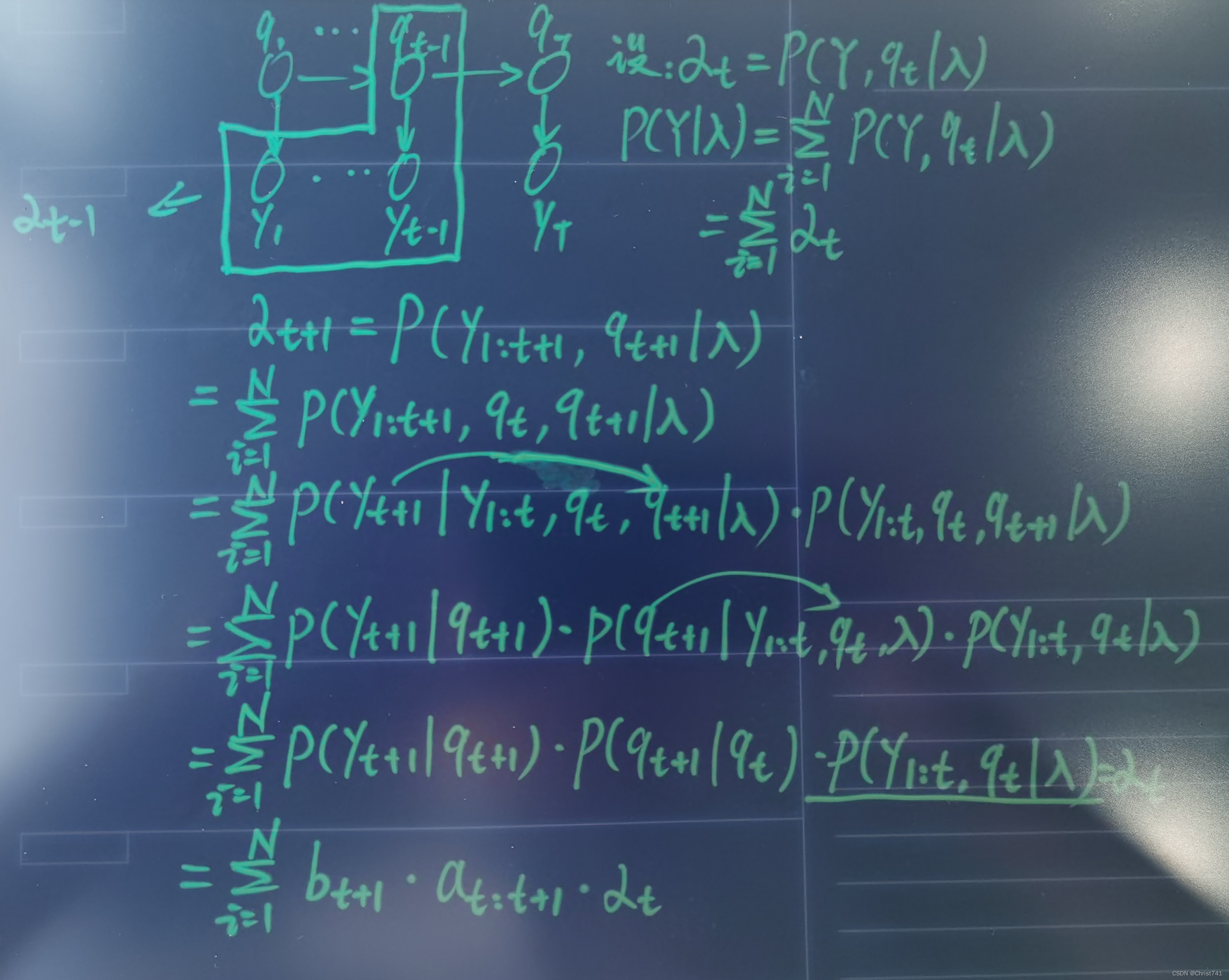
计算P(Y | λ) 方法之backward algorithm： 

设βt = P(yt+1:T | qt,λ)，q1取N个值；

右侧探索βt与βt+1的迭代关系，P(yt+1:T | qt+1,qt) = P(yt+1:T | qt+1)这里根据概率图关系，与qt无关；

通过多次迭代求得β1后得出P(Y | λ)。

求参问题-EM算法

Expectation—Maximization：迭代每一时刻的参数；

数据信息X->观测变量Y，隐变量Z->状态变量Q，迭代参数Θ->hmm参数λ；

这里通过拉格朗日乘子法对π求条件偏导，参数a,b求解方法一样，此处省略。

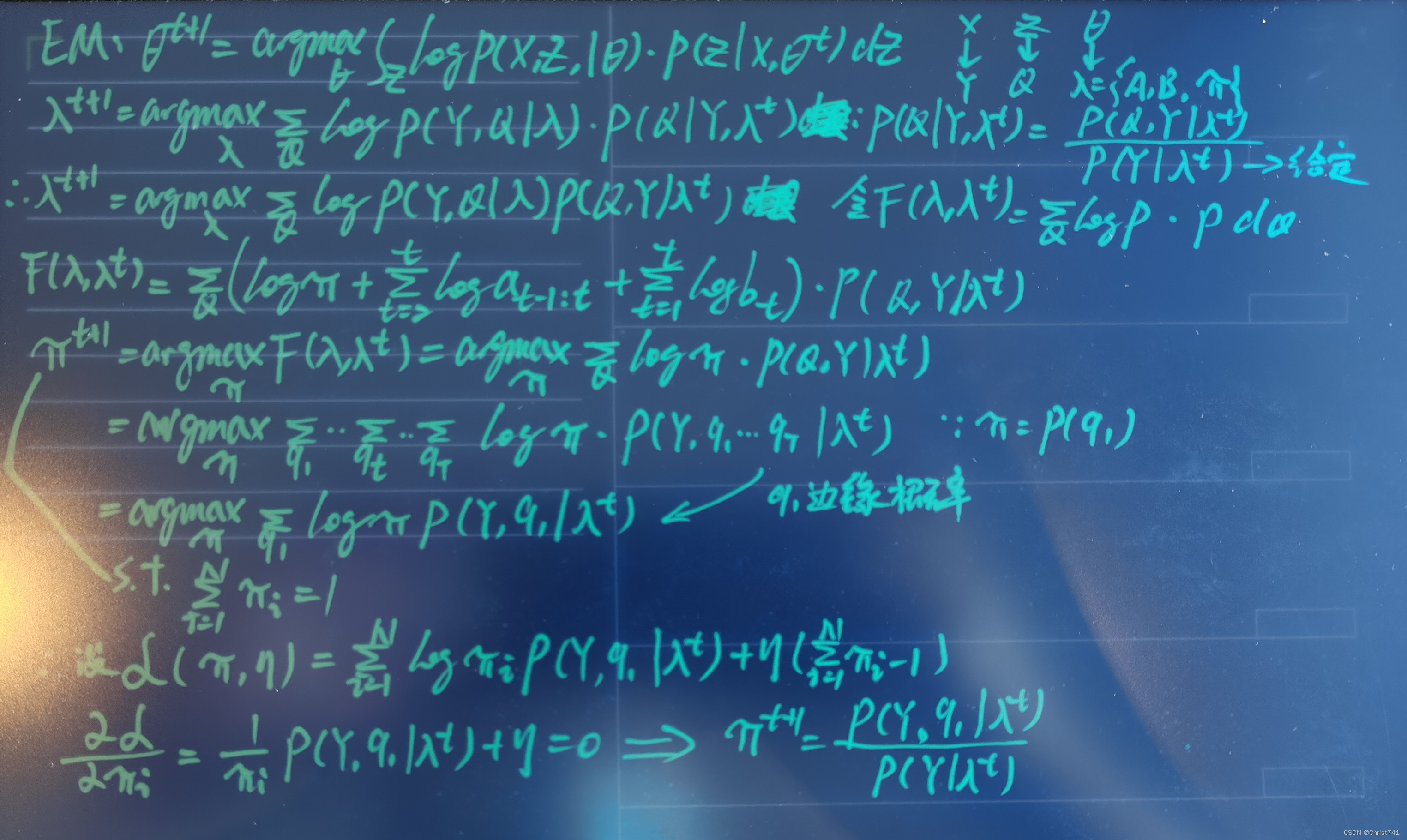
EM算法公式推导

由高斯混合模型引入EM迭代算法，GMM加入隐变量Z不改变边缘概率P(xi)；

迭代需要满足下一时刻参数对应的概率必须>=前一时刻的概率，

即:logP(x | Θg+1) >= logP(x | Θg)，加入隐变量Z，并在Z概率分布上积分；

求得logP(X | Θ） = Q(Θ​​​​​​​,Θ​​​​​​​g) - H(Θ​​​​​​​,Θg)；

因为H(Θ​​​​​​​g,Θ​​​​​​​g)-H(Θ​​​​​​​,Θg)>=0，即下一时刻H还<=上一时刻H，相当于减了一个更小的H，所以直接舍去H，只对Q(Θ​​​​​​​,Θg)求最大值即可。（因为- log是凹函数，由琴生不等式可知：函数的期望>=期望的函数值，所以得出H(Θ​​​​​​​g,Θ​​​​​​​g)-H(Θ​​​​​​​,Θg)>=0）

广义EM：hmm或者gmm都是特定条件下的应用EM算法，隐变量满足高斯分布或者马尔可夫性质，广义的EM算法对于拟合分布q，在p分布复杂情况下，要求q尽量逼近真实分布p。在对q(z)分布积分后，p(x)公式拆分为ELBO和kl散度。E-step是给定参数Θ后，求出该参数下最拟合p的q，M-step是求出给定拟合好的q下的最优参数Θ。！广义的EM中，ELBO的H[q(z)]=∫q(z)log1/q(z)dz就是q(z)的熵H[q(z)]，而在特定模型下，其实就因为模型的性质使得H[q(z)]可以约去。

解码问题

给定观测序列Y和参数λ，求使得概率最大的状态变量序列Q，其实就是个 求最大概率的动态规划问题。每个时刻的q都有N个取值。

写的有点匆忙，有问题可以+v: llllChrist，注明csdn。