朴素贝叶斯详解——从条件概率的引入到朴素贝叶斯的形成再到模型的训练

1、用案例引出条件概率

用类似抽签的案例
换句话来说就是先抢和后抢的概率如何。
讨论：
有人说先抢第一个人中的概率是1/47，第二个人抢的概率是1/46，依次下来，越后面的人概率是越大的。这是错的，为什么呢，因为在每一次抽的情况下我都要考虑，前一个人不中概率是多少，然后才能轮到下一个人抢是不是，算一下概率。

我们总共进行了n轮事件，$A_{\mathrm{n}-1}$代表“第n-1轮不中”

事件$B_{\mathrm{n}}$代表“第n轮抽中”

假设在第5轮我一定想要100元，可能性多大？

就是要列出当n=5时，发生的概率，那么要算n=5的前提，必须就是n=1、2、3、4都不中。

∴$P(\overline{A_1}\overline{A_1}\overline{A_1}\overline{A_1}{B}_5)=P(\overline{A_1})\cdot P(\overline{A_2}|\overline{A_1})\cdot P(\overline{A_3}|\overline{A_2}\overline{A_1})\cdot P(\overline{A_4}|\overline{A_3}\overline{A_2}\overline{A_1})\cdot P(\overline{A_5}|\overline{A_4}\overline{A_3}\overline{A_2}\overline{A_1})$

∴$P(\overline{A_1})=\frac{46}{47}$

当A1抽完之后，那么就还剩下46个，除去1个中的，那么A2不中的概率就是45/46

$P(\overline{A_2}|\overline{A_1})=\frac{45}{46}$

以此类推

$P(\overline{A_3}|\overline{A_2}\overline{A_1})=\frac{44}{45}$

$P(\overline{A_4}|\overline{A_3}\overline{A_2}\overline{A_1})=\frac{43}{44}$

那么最后

$P(\overline{A_5}|\overline{A_4}\overline{A_3}\overline{A_2}\overline{A_1})=\frac{1}{43}$

就是说无论抽多少此可以发现，相乘之后，中间的都会被约掉仍然是1/47，所以无需纠结。

2、条件概率引出贝叶斯

以硬币为例正面为X，反面为Y
A=“至少有一次为X”
B=“两次都为同一面”

列出样本空间，S为总的样本空间
S={XX,XY,YX,YY}
A={XY,XX,YX}
B={XX,YY}

那么A发生的条件下B发生的概率是多少？

对比AB可以看出

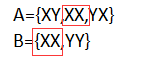
P(B|A)=1/3

S对比A、B，容易看出
P(A)=3/4，P(B)=1/2

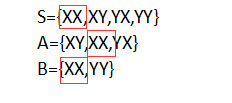
P(AB)=1/4

∴可以发现

$P(B|A)=\frac{P(AB)}{P(A)}=\frac{1}{3}$

∵
$P(AB)=P(B|A)P(A)$

变形一下

$P(BA)=P(A|B)P(B)$

又∵

$P(BA)=P(AB)$

代入

$P(B|A)=\frac{P(AB)}{P(A)}=\frac{1}{3}$

∴

$P(B|A)=\frac{P(A|B)P(B)}{P(A)}=\frac{1}{3}$
也就是贝叶斯公式

3、朴素贝叶斯基本原理

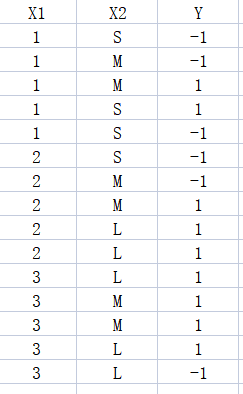
假设黑点为0，黄点为1，随便给一个点，判断P(X1,X2)的概率，若P1(X1,X2)>P0(X1,X2)，那么给出的点就归类在1标签，反之也如此。

那么当P(X1,X2…Xn)为联合概率，也是如此。

就是说给定了的这些数据特征怎么样去计算它属于某一类别的联合概率是多少的问题。

4、训练数据

$$P(B|A)=\frac{P(A|B)P(B)}{P(A)}$$
那么可以写成
$$P(y_i|x)=\frac{P(x|y_i)P(y_i)}{P(x)}$$
其中i表示分了多少类，比如分-1和1就是两类

P(AB)表示联合概率，如果两个是独立的，那么会等于P(A)·P(B)
那么就会得出
$$P(AB|y)=P(A|y)P(B|y)$$

其中从x来看，可能是多维的特征向量，就是说x会为（x1,x2,x3,…xn），那么当它们独立，就会得出：

$$P(y_i|x_1,x_1,x_1,...,x_n)=\frac{P(x_1|y_i)P(x_2|y_i)P(x_3|y_i)...P(x_n|y_i)}{P(x)}$$
那么假如给定数据判断=1的概率是多少时，然后再判断=-1的概率，算出来的概率都会除去P(x)，所以就把P(x)忽略掉了，仅仅是需要比较大小，而并不是算特定的值。

$$P(y_i|x_1,x_1,x_1,...,x_n)=P(x_1|y_i)P(x_2|y_i)P(x_3|y_i)...P(x_n|y_i)$$

例子：


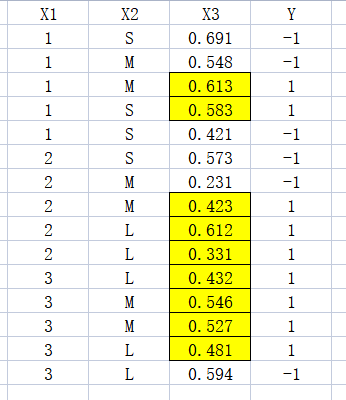
对于当出现0的情况，如果出现某一个值为零，那么总体概率相乘也就会等于0，这是不切实际的，只可能无限接近于0，就会引入拉普拉斯修正。

先验修正：
$$P(y)=\frac{|D_y|+1}{|D|+N}$$
似然修正：
$$P(x_i|y)=\frac{|D_{y,x_i}|+1}{|D_y|+N_i}$$
$$N_i$$ 表示第i个属性的可能取值

处理连续型数据

假设
$$P(\mathrm{y}=1|1,S,0.48)=P(x_1=1|y=1)P(x_2=S|y=1)P(x_3=0.48|y=1)P(y=1)$$
$$P(\mathrm{y}=1|1,S,0.48)=P(x_1=1|y=-1)P(x_2=S|y=-1)P(x_3=0.48|y=-1)P(y=-1)$$
那么主要是求x1=0.48的时候该怎么求？

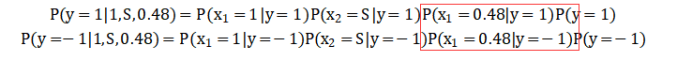
$$P(x_i|y)=\frac{1}{\sqrt{2\pi {\sigma }_{y,i}^2}}\exp (-\frac{{(x_i-{\mu }_{y,i})}^2}{2{\sigma }_{y,i}^2})$$

其中方差：${\sigma }_{y,i}^2$

均值：${\mu }_{y,i}$

就是将X1=0.48代入公式，然后根据y=1的值或者y=-1条件下的值求均值和方差，再代入公式得出结果。