期刊编辑总结：4个医学研究中常见的统计分析错误，值得学习

今天这篇推文和诸位分享一篇社论文章，题为：“Avoiding pitfalls in conducting hand surgery research – potential consequences of common errors in statistical analyses”。

这篇社论演示了四种常见统计学分析错误以及可能产生的后果：1.不必要的二值化处理；2.忽视数据聚类；3.将预测建模方法用于检验独立关联；4.违反逻辑回归的假设。

尽管它探讨的是手外科研究中的相对常见的统计分析错误，但其实在医学研究中是通用的。

并且，文章中的示例源自编辑在审稿或协助研究者答疑时经常遇到、并持续关注到的情形。

值得我们学习！

---

1

连续数据的二值化处理

连续数据的二值化是将连续变量分成两组的过程。连续数据的二值化处理：

• 会降低研究的统计效能，使其更难检出真实效应；

• 同时会低估数据集的变异性，可能导致我们在无真实效应时仍接受备择假设；

• 此外，还会丧失识别非线性关系的能力。

示例

某项研究旨在确定桡腕腕底关节置换术后前20周内疼痛水平的变化。

疼痛水平采用VAS量表测量，分值范围为0（最佳）至100（最差）。

共有100位患者在术后不同时间点各填测一次VAS量表，因此数据集中共有100条观测值。

为了比较术后短期与长期的疼痛差异，我们将随访时间按平均值一分为二，将100条观测分为“短期组”和“长期组”。

随后对两组VAS分数进行独立样本t检验，结果显示术后短期与长期疼痛水平无显著差异（均值差 = −0.40，95%置信区间 −5.60至6.40）。

然而，通过将时间变量二值化，我们完全忽略了数据中可见的“U 型”关系（见图 1）。显然，患者在恢复正常日常活动时疼痛会加剧，随后才会有所缓解。

在这种情况下，我们可以在回归模型中为时间变量额外添加一个指数项来对该“U 型”关系进行建模，而使用 t 检验则无法实现。该指数时间变量在统计学上显著（β2= −37.13，p = 0.01），正好印证了这一非线性关系。

有时，当研究者在数据中看到“U 型”趋势时，他们会选择不再二值化，而是将连续变量分为三类。

虽然这比二分法更好一些，但仍非最佳方案。

以我们的示例为例，假如我们将数据按第 33 和第 66 百分位分为三组，然后对三组两两进行 t 检验，结果仍会得出随访时间对疼痛水平无显著影响的结论。

因此，仅将 VAS 值分为三类也无法充分考虑该倒 U 型趋势。最合适的分析方法仍是回归分析。

这个示例表明，不必要的数据分组会导致信息丢失，进而可能导致错误结论。

2

忽视数据聚类

数据聚类是指数据集中可能存在的独立观测值之间的相关性。

当对数据集中的多个观测值进行分组时，就会发生数据聚类，这些观测值之间存在相关性，因此比组外的观测值更相似。

忽视数据聚类是一个极其常见的问题，我们在此将进一步阐述可能带来的后果。

示例

在手外科研究中，数据往往天然聚类：手指聚于手，双手又聚于同一患者。当研究涉及多根手指时，数据聚类现象尤为明显。

例如，有研究比较了经皮针状筋膜切开术与有限筋膜切除术在 Dupuytren 病患者挛缩矫正中的效果。

研究共纳入 55 名患者的 55 只手中的 118 根手指，研究者使用线性回归模型分析数据，结果发现有限筋膜切除术在矫正挛缩方面的效果显著优于经皮针状筋膜切开术。

然而，在这种情况下，线性回归并未考虑到因同一患者纳入多根手指而产生的数据聚类。

如果对相同数据集采用线性混合效应模型——这是一种能够考虑观测值间相关性的统计分析技术——则两种手术方法间的这一统计学显著差异便不再存在。

当我们关注数据的可变性（即标准误）时，其原因可以清楚地看到。

线性回归模型假设所有观测值彼此独立，就如同它们分别来自 118 位不同患者，因此低估了标准误。

而线性混合效应模型解释了多个观测值之间存在相关性的事实。由于相关观测值提供的信息相对有限，该模型估计出的标准误高于线性回归模型。

这一更大的标准误解释了为何在采用混合效应模型分析时，两种手术方法的差异不再具有统计学意义。

因此，当数据存在聚类结构时，应使用混合效应模型或广义估计方程等方法进行分析。

3

将预测建模方法用于检验独立关联

回归分析是一类基于变量间关系建模的统计方法，既可用于线性关系，也可处理多种非线性关系，因此极具灵活性，可回答多样的研究问题。

然而，不同研究问题需对应不同的分析策略。

一个常见错误是研究者采用预测模型的方法来探讨 x 与 y 之间是否存在关联。

下面的示例将演示二者的区别。

示例

某研究旨在评估哪些代谢综合征标志物与腕管综合征（CTS）具有独立关联性。

研究人员计划进行逻辑回归分析来研究这种关系，这将是合理的选择。

首先，他们进行了单变量回归分析，分别评估各指标的效应。所考察的变量包括腰围、甘油三酯、高密度脂蛋白（HDL）水平、低密度脂蛋白（LDL）水平、高血压，以及潜在混杂因素年龄和性别。

仅将单变量分析中 p <0.20 的变量纳入多变量模型。

多变量模型显示，年龄和HDL水平对CTS发生风险的影响有统计学意义，其他变量无统计学意义。

由于仅基于 p 值进行变量筛选，潜在混杂因素——性别未被纳入模型。

通过比较在未调整变量Z和调整Z之后的模型中，其暴露因素X的回归系数（β）或OR值的变化程度（一般设10%），评估Z是否为潜在的混杂因素。

经验法则认为，若效应量变化超过 10%，则应将该混杂因素纳入模型。

在评估各个指标的单因素回归模型中，分别调整年龄和性别，几乎所有关联中年龄和性别均被识别为潜在混杂因素。

当我们将年龄和性别同时作为混杂因素加入模型后，HDL 和高血压的比值比发生了较大变化。

基于此模型，我们可以得出结论：在调整年龄和性别后，没有任何一种指标对发生 CTS 风险具有独立影响。

此示例表明，在研究关联时，即便混杂因素的 p 值并不显著，它们仍可能影响所关注效应，从而改变研究结论。

使用预测建模方法来确定关联时的另一个不良影响是，一些感兴趣的变量不会被纳入多变量模型——在这个示例中也出现了这种情况。因此，研究者无法完整回答哪些指标与CTS具有独立关联这一研究问题。

虽然这种方法（模型选择，无论是否采用逐步筛选）经常在教科书中描述，但它并不适合研究x和y之间的关联。

重要的是要意识到，基于p值或模型拟合度来选择纳入模型的变量，是一种用于找到包含最少变量的最佳预测模型的最好的方法。

然而，用于预测的回归模型与用于判断关联是否存在的回归模型，其目的大相径庭。

所以，在研究关联时，应首先基于概念框架而非 p 值来决定纳入哪些变量；因此，所选变量应与所研究的关联具有临床相关性。

4

忽视统计方法的假设

大多数统计方法都基于一定的假设，这些假设决定了效应估计的有效性；统计结果的可靠性也取决于这些假设是否得到满足。

然而，有研究显示，在六大医学期刊发表的随机对照试验中，仅有 21% 在统计分析方案或最终报告中说明了如何检验这些假设[2]。这可能意味着要么测试结果未被报告，要么根本未进行测试。

当假设被忽视或违反时，结果可能产生误导，并可能改变研究结论。

我们想通过一个示例来演示这一点，其中使用逻辑回归分析数据。

示例

研究者模拟了一组研究数据，除CTS结局外，还收集了贫困程度、教育水平、就业状况、收入、年龄和性别等信息。应用逻辑回归评估社会经济地位与CTS发生风险之间的关联。

逻辑回归分析的常见假设包括：

（1）观测值相互独立；

（2）无极端离群值；

（3）自变量之间相关性低或无（即无多重共线性）；

（4）自变量与因变量对数几率（logit）之间存在线性关系。

前两项假设较为常见且易于理解，此处我们将重点展示后两项假设的检验。

1.检验是否违反“自变量间无相关性”假设

自变量间相关性可通过计算方差膨胀因子（VIF）来评估：当 VIF > 5 时，表明存在较高相关性。

本例中，贫困指数、教育水平、就业状况和收入的 VIF 值分别为 6.32、7.42、1.62 和 13.30。

在模型中逐一剔除变量后，我们发现贫困指数和教育水平与收入高度相关。

这将带来问题：

（1）自变量之间高度相关时，就难以区分某一变量对结果的独立影响——在本例中，即难以将贫困指数或教育水平的效应与收入的效应区分开来。

（2）同时，这也会增加模型的不确定性，导致置信区间变宽。

因此，当变量取值稍有变化时，效应估计（此处为回归系数）可能发生较大变化，换言之，其可靠性不足。

如表 4B 所示，在同一模型中对收入变量仅做微小调整，模型估计值便显著改变。

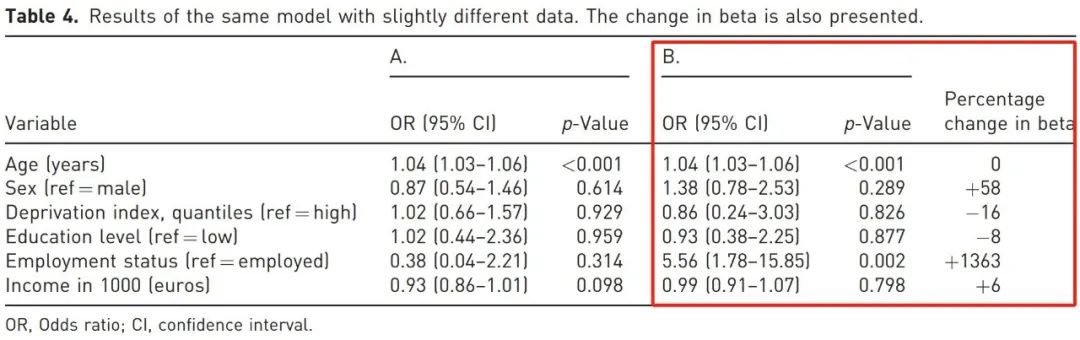
解决之道是从模型中移除部分高度相关的变量，或尝试将这些变量合并。需要注意的是，多重共线性仅在评估关联时才是问题；若目的是构建预测模型，则无需过分担心。

2.自变量与因变量对数几率（logit）之间存在线性关系

与假设自变量与连续因变量之间存在线性关系的线性回归不同，逻辑回归针对的是二分类因变量。为此，将几率（结局发生的概率与不发生的概率之比）转换为结果为0或1（使用对数进行转换），也称为logit。

这样便可用“S 型”曲线对结果进行建模。由此可见，线性回归和逻辑回归在“线性关系假设”上具有相似之处。

假设收集了外科医生的经验（从业年限）与桡骨远端骨折手术后并发症风险的数据。自变量“外科医生经验”以年为单位表示，因变量“并发症发生”为二分类结果。在这种情况下，可以使用逻辑回归进行分析。

在将经验变量直接加入模型之前，必须先检验各项假设，其中之一就是自变量与因变量 logit 之间的线性关系（如上所述）。

如何评估这一假设？

首先，可将外科医生的从业年限分为若干类别（对连续自变量进行分组）。

其次，计算每一类别中发生并发症的患者数与该类别患者总数之比（p）。

对每个类别都应重复上述步骤。

第三，按如下公式计算 logit 值。

第四，将该公式的计算结果（logit）作为纵轴，将外科医生经验的不同类别（连续自变量）作为横轴绘图。

如图所示，该图表明（已分组的）连续自变量与结局的 logit 之间呈线性关系。

如果在此图中明显偏离线性，则说明该假设被破坏，无法将外科医生经验年限作为连续自变量应用于逻辑回归。

对此，可采取的简单解决方案是以不同方式对自变量进行分组；如果担心这样可能丢失重要信息，例如存在（倒）U 型关系，则可能需要使用更复杂的分析技术，例如样条回归，来进行建模分析。

通过上述示例，希望能加深诸位对研究中统计分析常见错误及其潜在后果的认识。这些错误确实真实存在且相对常见，必须予以重视。

作为临床医生和科学工作者，我们有责任为所提出的研究问题提供可靠且诚实的答案，其中也包括避免在统计方法中出现错误。

参考文献：

[1]Broekstra DC, Bonhof-Jansen EEDJ, Marks M. Avoiding pitfalls in conducting hand surgery research - potential consequences of common errors in statistical analyses. J Hand Surg Eur Vol. 2025 Apr 12:17531934251330978. doi: 10.1177/17531934251330978. Epub ahead of print. PMID: 40219851.

[2]Nielsen EE, Nørskov AK. Assessing assumptions for statistical analyses in randomised clinical trials. BMJ Evid Based Med. 2019 Oct;24(5):185-189. doi: 10.1136/bmjebm-2019-111174. Epub 2019 Apr 4. PMID: 30948454.

---

关于郑老师团队及公众号

大型医学统计服务公众号平台，专注于医学生、医护工作者学术研究统计支持，我们是你们统计助理

我们开展对临床预测模型、机器学习、医学免费数据库NHANES、GBD数据库、CHARLS、孟德尔随机化方法、MIMIC 一对一R语言指导开展统计分析（一年内不限时间，周末、晚上均统计师一对一指导）。

①指导学习R语言基本技巧

②全程指导课程学习

③课程R语言代码运行bug修复

④支持学员一篇SCI论文的数据分析

1对1R语言指导详情介绍

详情联系助教小董咨询（微信号aq566665）