矩阵余子式：史上最通俗易懂的讲解！！

1. 余子式

假设我们有一个 $n\times n$ 的矩阵 $A$:

$$A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right]$$

想象这个矩阵是一块蛋糕。余子式就像是从这块蛋糕中"切掉"某一行和某一列后剩下的部分。

具体来说:

1. 选定矩阵中的某个元素 $a_{ij}$（第 $i$ 行第 $j$ 列的元素）
2. 把这个元素所在的整行和整列都划掉
3. 剩下的元素组成的新矩阵的行列式，就是元素 $a_{ij}$ 的余子式，记作 $M_{ij}$

例如，对于一个 $3\times 3$ 的矩阵：

$$A=\left[\begin{array}{ccc}2& 3& 1\\ 4& 1& 3\\ 2& 5& 2\end{array}\right]$$

如果我们要求元素 $a_{11}=2$ 的余子式，就要划掉第1行和第1列：

$$M_{11}=\left|\begin{array}{cc}1& 3\\ 5& 2\end{array}\right|=1\cdot 2-3\cdot 5=-13$$

余子式在计算行列式、求逆矩阵等场景中非常重要。例如，它与代数余子式 $C_{ij}$ 有如下关系：

$$C_{ij}=(-1{)}^{i+j}{M}_{ij}$$

这就像是在玩一个数学版的"九宫格"游戏，每次我们都要移除一行一列，然后计算剩余部分的行列式值。

2. 矩阵余子式可视化

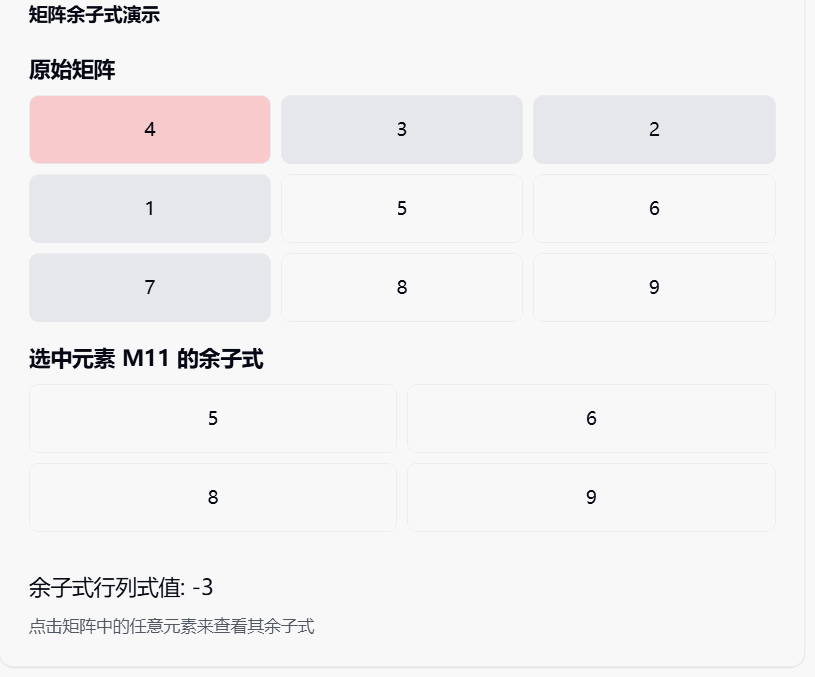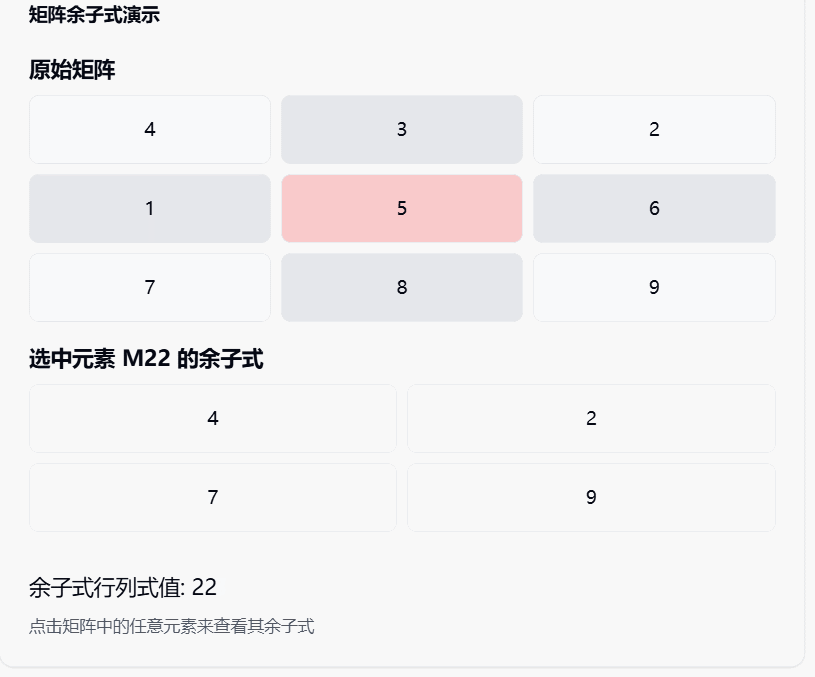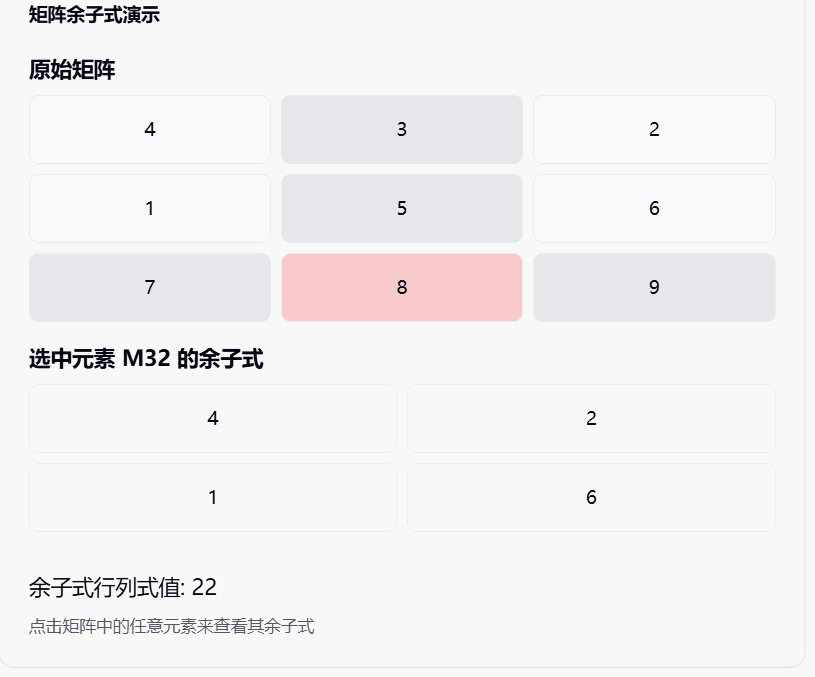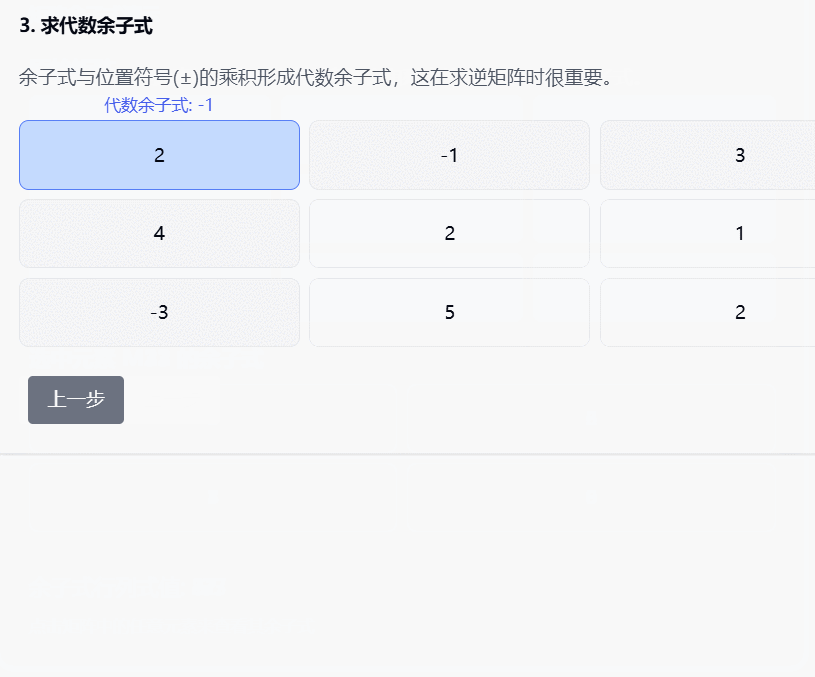
让我来解释一下这个可视化工具是如何工作的：

1. 上方显示的是一个3×3的示例矩阵
2. 点击矩阵中的任何一个元素，就可以看到该元素对应的余子式
3. 当你选择一个元素时：
   • 该元素所在的行和列会被标记为灰色
   • 选中的元素会被标记为红色
   • 下方会显示去掉该行和该列后剩余的2×2矩阵，这就是余子式
   • 同时还会计算出这个2×2余子式的行列式值

余子式的计算过程是：

1. 选定矩阵中的某个元素aᵢⱼ
2. 删除这个元素所在的第i行和第j列
3. 剩下的元素组成的子矩阵就是余子式

例如，如果你点击左上角的元素(1,1)，那么：

• 删除第1行和第1列
• 剩下的2×2矩阵就是余子式
• 这个2×2矩阵的行列式值就是余子式的值

你可以尝试点击不同的元素，观察对应的余子式是如何变化的。这有助于理解余子式的概念。

需要我进一步解释某个具体部分吗？或者你想了解更多关于余子式在矩阵计算中的应用？

3. 余子式在矩阵中的作用

让我用一个生动的比喻来解释余子式的作用。

想象矩阵是一个大厅里的座位安排，比如一个3x3的矩阵就像是9个座位排成3排3列。余子式就像是在这个座位安排中"屏蔽"某个座位时的情况。

余子式在矩阵中有几个重要作用：

1. 求行列式

   • 余子式就像是矩阵的"支柱"，帮助我们逐步拆解大矩阵的行列式
   • 通过每个元素与其对应的余子式的行列式相乘，我们可以计算出整个矩阵的行列式
   • 这个过程就像是把一个复杂的结构拆分成更小的部分来理解

2. 求逆矩阵

   • 余子式是求逆矩阵的关键工具
   • 每个元素的余子式（配合正负号）形成代数余子式
   • 所有代数余子式组成的矩阵（伴随矩阵）帮助我们找到原矩阵的逆

3. 特征值计算

   • 在求解特征值时，余子式帮助我们理解矩阵的内部结构
   • 它像是矩阵的"骨架"，揭示了矩阵的基本性质

4. 克莱姆法则应用

   • 在解线性方程组时，余子式帮助我们用一种优雅的方式得到解
   • 每个未知数的解都可以通过相应的余子式来表达

在上面的可视化演示中：

• 你可以看到矩阵中每个位置的元素
• 当我们选择一个元素时，它所在的行和列会被突出显示
• 这些被删除的行和列就像是被"屏蔽"的部分
• 剩下的元素形成的小矩阵就是余子式

通过这种方式，余子式就像是矩阵的"透视图"，让我们能够从不同角度理解矩阵的结构和性质。它是连接矩阵各种重要概念的桥梁，比如：

• 行列式计算
• 矩阵求逆
• 线性方程组求解

4. 代数余子式详解

代数余子式是计算行列式和矩阵求逆时的重要概念。让我们从基础开始逐步理解：

1. 余子式的定义
   对于一个n阶矩阵A中的元素$a_{ij}$，它的余子式$M_{ij}$是指:

• 去掉$a_{ij}$所在的第i行和第j列后
• 剩余的(n-1)阶行列式

1. 代数余子式的定义
   代数余子式$A_{ij}$是在余子式$M_{ij}$的基础上，乘以系数$(-1{)}^{i+j}$：

$$A_{ij}=(-1{)}^{i+j}{M}_{ij}$$

1. 举个具体例子
   对于3阶矩阵：
   $$\left|\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right|$$

求$a_{11}$的代数余子式步骤：

• 首先求余子式$M_{11}$，即删除第1行第1列后的行列式：
  $$M_{11}=\left|\begin{array}{cc}{a}_{22}& a_{23}\\ a_{32}& a_{33}\end{array}\right|$$

• 然后乘以$(-1{)}^{1+1}=1$，得到代数余子式：
  $$A_{11}=\left|\begin{array}{cc}{a}_{22}& a_{23}\\ a_{32}& a_{33}\end{array}\right|$$

1. 代数余子式的应用

代数余子式主要用于：

a) 计算行列式（按行或列展开）：
$$det(A)=a_{i1}{A}_{i1}+a_{i2}{A}_{i2}+...+a_{in}{A}_{in}$$

b) 求逆矩阵：
$$A^{-1}=\frac{1}{det(A)}[A_{ij}{]}^T$$

1. 计算技巧

• 选择含零较多的行或列展开可以简化计算
• 记住$(-1{)}^{i+j}$的正负交错规律：
  $$
  \begin{matrix}

• & - & + & - \

• & + & - & + \

• & - & + & - \

• & + & - & +
  \end{matrix}
  $$

5. $(-1{)}^{i+j}$的正负交错规律

这个规律是计算代数余子式时判断正负号的关键。我们可以通过一个表格来直观理解：

对于一个矩阵，设行标为i，列标为j，那么位置(i,j)的符号由$(-1{)}^{i+j}$决定。让我们写出前4行4列的情况：

$$\begin{array}{cccc}(1,1)& (1,2)& (1,3)& (1,4)\\ (2,1)& (2,2)& (2,3)& (2,4)\\ (3,1)& (3,2)& (3,3)& (3,4)\\ (4,1)& (4,2)& (4,3)& (4,4)\end{array}$$

计算每个位置的$(-1{)}^{i+j}$：

1. 第一行(i=1)：

   • (1,1): $(-1{)}^{1+1}=(-1{)}^2=+1$
   • (1,2): $(-1{)}^{1+2}=(-1{)}^3=-1$
   • (1,3): $(-1{)}^{1+3}=(-1{)}^4=+1$
   • (1,4): $(-1{)}^{1+4}=(-1{)}^5=-1$

2. 第二行(i=2)：

   • (2,1): $(-1{)}^{2+1}=(-1{)}^3=-1$
   • (2,2): $(-1{)}^{2+2}=(-1{)}^4=+1$
   • (2,3): $(-1{)}^{2+3}=(-1{)}^5=-1$
   • (2,4): $(-1{)}^{2+4}=(-1{)}^6=+1$

最终得到这样的正负交错表：

$$
\begin{matrix}

• & - & + & - \

• & + & - & + \

• & - & + & - \

• & + & - & +
  \end{matrix}
  $$
  

观察可以发现几个特点：

1. 对角线元素(从左上到右下)全为正号

   • 因为i=j时，i+j为偶数

2. 相邻元素符号相反

   • 因为相邻位置的i+j值相差1

3. 形成了棋盘格式的交错pattern

   • 第一个元素(1,1)为正
   • 横向交替变化
   • 纵向交替变化

实际应用时，不需要每次都计算$(-1{)}^{i+j}$，记住这个交错规律可以快速判断符号：

• 从"+"开始
• 相邻格子符号相反
• 呈棋盘格分布

这个规律对任意大小的矩阵都适用，只要按照同样的模式继续扩展即可。