双射： 史上最简单讲解！！

1. 双射的形象解释

双射是数学中一个重要的函数概念，我可以用一些形象的例子来帮助你理解。

双射（Bijection）是一种特殊的函数，它同时满足两个条件：

1. 单射（Injection）：每个不同的输入都映射到不同的输出——就像每个人都有唯一的指纹。
2. 满射（Surjection）：函数的值域中每个元素都能通过至少一个定义域中的元素映射得到——就像每个座位都有人坐。

形象例子

例子1：班级座位安排

想象一个班级有30名学生和30个座位：

• 如果每个学生都有且仅有一个固定座位，并且每个座位都被分配给了一名学生，这就是一个双射关系。
• 这意味着：没有学生需要站着，也没有座位是空的，而且没有两个学生共享同一个座位。

例子2：钥匙和锁

想象一组锁和钥匙：

• 如果每把钥匙只能开一把特定的锁（单射）
• 且每把锁都有一把能开它的钥匙（满射）
• 那么钥匙到锁的映射就是双射。

例子3：扑克牌配对

想象一副扑克牌分给两个人：

• 如果每个人都拿到26张不同的牌，这是一个双射
• 每张牌只能在一个人手里（单射）
• 所有牌都被分配出去（满射）

数学表示

对于函数 $f:X\to Y$:

• $f$ 是双射，当且仅当对于每个 $y\in Y$，恰好存在一个 $x\in X$ 使得 $f(x)=y$

双射的重要性

双射表明两个集合之间有一一对应的关系，这在数学中非常重要，因为：

• 它确立了两个集合之间的"大小相等"
• 双射函数总是有逆函数
• 在计数问题中，如果我们可以建立双射，我们就可以通过计算一个集合的大小来确定另一个集合的大小

2. 进一步形象讲讲满射

我来用形象的方法解释满射这个数学概念。

想象你有两个集合，我们把第一个集合叫做"出发地"，第二个集合叫做"目的地"。满射就像是从出发地发射箭矢到目的地的过程:

主要特点:

1. 每个"目的地"点都必须至少被一支箭击中。这就是满射最关键的特征 - 目标集合中不能有"漏网之鱼"。

2. 允许多支箭射向同一个目标。也就是说,一个"目的地"可以被多个"出发地"的元素对应。

举个具体的例子:
想象你有一个投票箱(目的地集合)有3个选项:A、B、C
有5个投票人(出发地集合):小明、小红、小李、小张、小王

如果:

• 小明和小红都投了A
• 小李投了B
• 小张和小王投了C

这就构成了一个满射,因为:

1. 每个选项(A、B、C)都至少获得了一票
2. 允许A和C各自获得多票

相反,如果没有人投C,即使A、B都有人投,也不构成满射,因为C这个"目的地"没有被任何箭矢击中。

3. react可视化组件讲解双射和满射

1. 满射（Surjective）的特点：

   • 目标集合中的每个元素都至少被一个源集合元素映射到
   • 允许多个源集合元素映射到同一个目标元素
   • 形象理解：每个"目标"都必须至少被一个"箭头"指向

2. 单射（Injective）的特点：

   • 每个目标集合元素最多只能被一个源集合元素映射
   • 不允许多个源集合元素映射到同一个目标元素
   • 形象理解：每个"目标"最多只能被一个"箭头"指向

3. 双射（Bijective）的特点：

   • 既是满射又是单射
   • 源集合和目标集合元素个数必须相等
   • 每个源集合元素恰好映射到一个目标元素
   • 每个目标集合元素恰好被一个源集合元素映射
   • 形象理解：每个"目标"都恰好被一个"箭头"指向

你可以通过点击箭头来切换它们的状态，实验不同的映射关系。组件会实时显示当前映射是否满足满射、单射和双射的条件。

4. 形象讲讲， 为什么矩阵会和双射建立联系

我来用形象的方法解释矩阵和双射的关系。

想象一个变换矩阵就像是一个"变形机器"：

1. 输入空间到输出空间的映射：

• 矩阵是把一个向量变成另一个向量的"规则"
• 比如你输入向量 (x,y)，矩阵会通过线性变换把它变成新的向量 (x’,y’)
• 这就像是一个"函数"，输入集合是原始向量空间，输出集合是变换后的向量空间

1. 可逆矩阵与双射的对应：

• 一个 n×n 的可逆矩阵就像是一个"完美的变形机器"：
  • 每个输入向量都会变成唯一的输出向量（单射性质）
  • 每个输出向量都能通过某个输入向量得到（满射性质）
  • 这就构成了一个双射！

举个具体的例子：
想象一个 2×2 的旋转矩阵，它把平面上的点旋转90度：

[0  -1]
[1   0]

这个矩阵的作用就像是：

• 把点 (1,0) 变成 (0,1)
• 把点 (0,1) 变成 (-1,0)
• 把每个点都旋转90度

这是一个双射因为：

1. 每个点都会被旋转到一个新位置（满射）
2. 不同的点旋转后一定在不同位置（单射）
3. 每个点都能通过反旋转90度找到它的原始位置（可逆性）

相反，如果是一个不可逆矩阵：

[1  1]
[2  2]

它会把很多不同的点"压扁"到同一条直线上：

• 多个不同的输入点会变成同一个输出点（失去单射性）
• 有些点永远不可能是任何输入点的像（失去满射性）
• 这就不是双射了！

这就是为什么：

• 可逆矩阵 ⟺ 双射线性变换
• 行列式不为零 ⟺ 可逆 ⟺ 双射
• 变换前后空间维数保持不变

你现在能更好地理解矩阵和双射的联系了吗？如果需要，我可以用更多具体的例子来解释。

5. 来个具体案例进一步讲讲

让我解释这个可视化工具中的三个典型例子：

1. 旋转矩阵 [0 -1; 1 0]：

• 这是一个90度旋转变换
• 把每个点都逆时针旋转90度
• 是双射因为：
  • 每个点都被旋转到一个新的唯一位置（单射）
  • 平面上的每个点都可以通过旋转得到（满射）
• 行列式 = 1，说明保持了面积不变

1. 缩放矩阵 [2 0; 0 2]：

• 把所有点扩大2倍
• 也是双射因为：
  • 不同的点变换后仍然不同（单射）
  • 可以通过除以2得到任何点的原像（满射）
• 行列式 = 4，表示面积扩大了4倍

1. 投影矩阵 [1 1; 1 1]：

• 把所有点投影到y=x直线上
• 不是双射因为：
  • 不同的点会被压缩到同一个点上（失去单射性）
  • y=x直线外的点不可能是任何点的像（失去满射性）
• 行列式 = 0，说明降低了维度

通过这个可视化工具，你可以：

1. 直观地看到点在变换前后的位置变化
2. 理解为什么某些矩阵变换是双射而其他不是
3. 观察行列式与双射性质的关系

6. 满射和双射的关系

对于映射，角度确实不同。让我用更直观的方式说明：

1. 满射的角度：从"目标空间"的视角看

   • 关注点是目标集合上的每个元素是否都被"照顾到"了
   • 不在乎一个目标元素被多少个源元素映射
   • 就像是在玩"覆盖游戏"，确保目标集合的每个点都被覆盖到
   • 形象例子：老师分发糖果给学生，只要每个学生都至少拿到一颗糖就满足满射的要求，不管某些学生拿到多少颗

2. 双射的角度：同时关注"源空间"和"目标空间"

   • 既要满足满射（每个目标元素都被映射到）
   • 又要满足单射（每个目标元素最多只被一个源元素映射）
   • 形象例子：学校举办舞会，每个男生只能邀请一个女生，每个女生也只能被一个男生邀请，必须都配对成功才是双射

3. 在线性代数中的具体体现：

• 满射关注的是变换后是否"填满"了整个目标空间

  • 例如：矩阵的列空间是否等于值域空间
  • 变换后不会"缺失"任何维度

• 双射则额外要求变换是"一一对应"的

  • 矩阵必须是方阵
  • 行列式不为零
  • 没有信息的丢失或重叠

让我用代码来可视化这个差异：

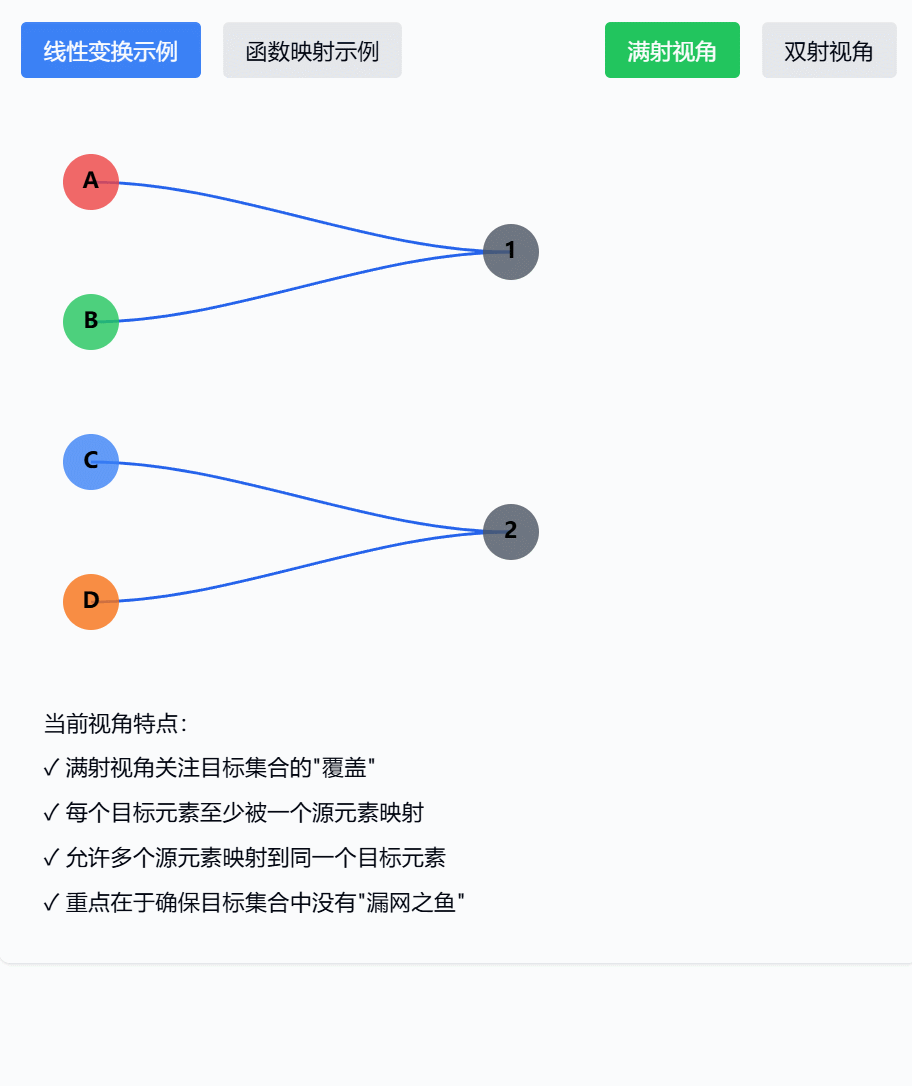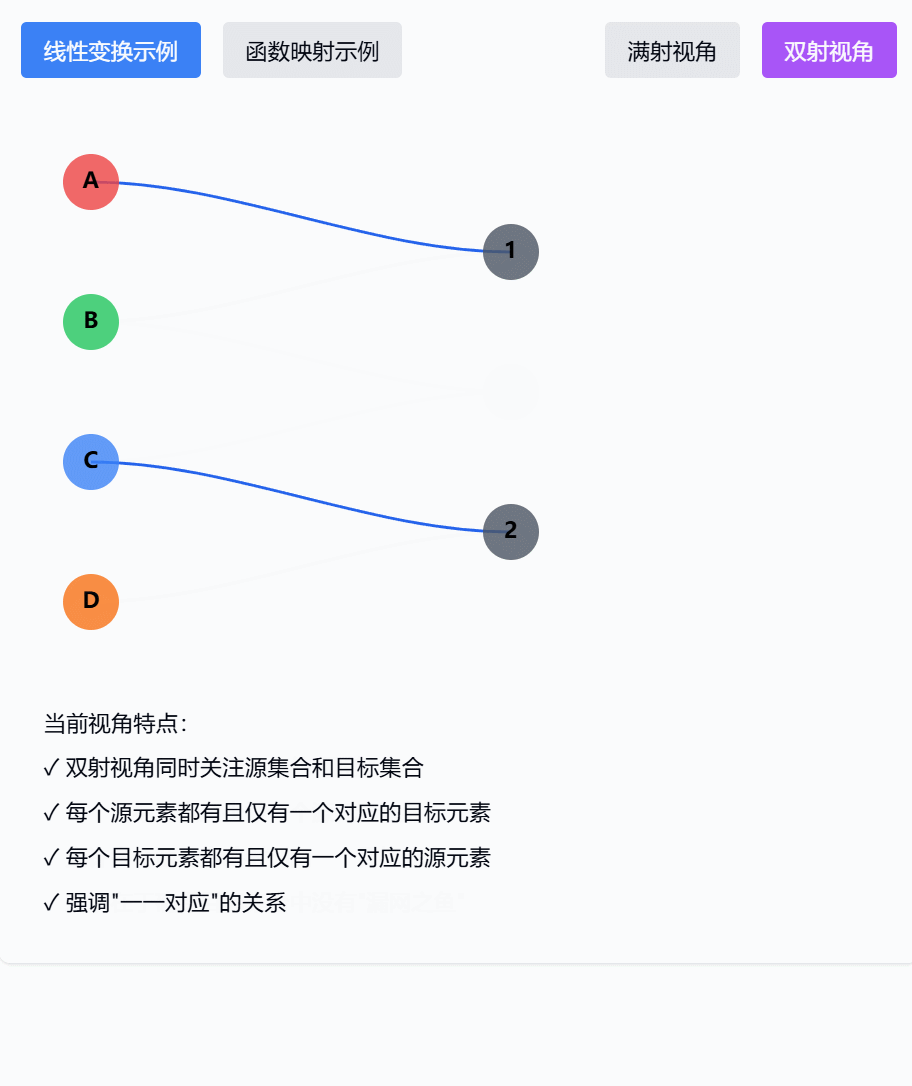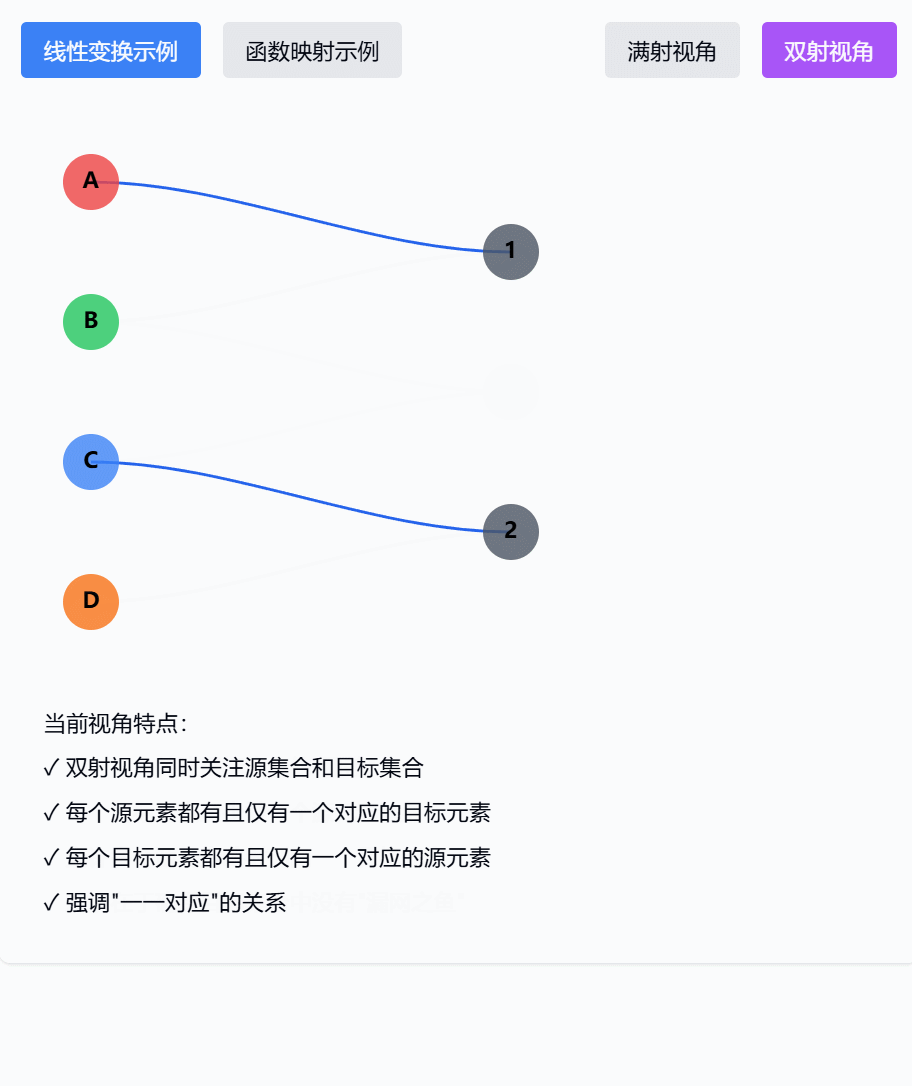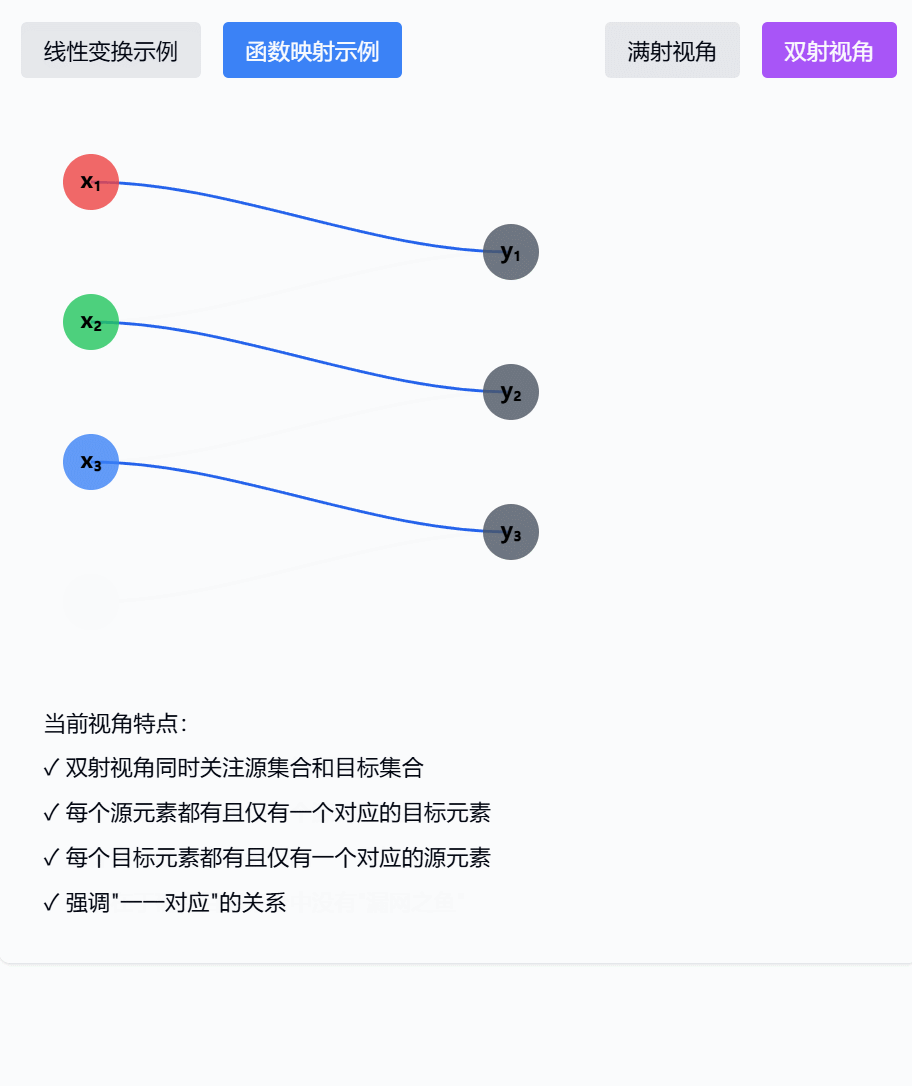
这个可视化组件展示了满射和双射在观察角度上的关键差异：

1. 满射的视角（点击"满射视角"按钮）：

• 从目标空间往回看
• 重点检查：是否每个目标元素都"被照顾到了"
• 不关心源元素是如何分配的
• 类似于"覆盖问题"

1. 双射的视角（点击"双射视角"按钮）：

• 同时关注源空间和目标空间
• 重点检查：
  • 源空间：每个元素都有去处
  • 目标空间：每个元素都有来源
  • 且都是唯一的对应关系
• 类似于"完美匹配问题"

1. 实际应用中的区别：

• 满射更关注"结果的完整性"
• 双射更关注"对应关系的完美性"
• 可以说双射的要求更严格，因为它在满射的基础上添加了单射的要求

7. 最终讲解

让我创建一个更清晰的可视化，明确标注源空间和目标空间，并进一步解释满射和双射的区别。

现在让我更清晰地解释源空间和目标空间的概念，以及满射和双射的不同视角：

源空间与目标空间

1. 源空间（Domain）：

   • 映射的出发点，也称为定义域
   • 在函数中表示为 f: X → Y 中的 X
   • 在矩阵变换中，是变换前的向量空间
   • 对应可视化中左侧的区域

2. 目标空间（Codomain）：

   • 映射的到达点，也称为陪域
   • 在函数中表示为 f: X → Y 中的 Y
   • 在矩阵变换中，是变换后的向量空间
   • 对应可视化中右侧的区域

不同类型的映射从不同角度看问题

1. 满射的视角（从目标空间看）：

   • 核心问题：目标空间中的每个元素是否都被"覆盖"？
   • 满射条件：目标空间中的每个元素都至少有一个源空间元素映射到它
   • 不关心：多个源元素映射到同一目标元素是允许的
   • 线性代数中：变换没有降低维度，变换后的向量能够"填满"整个目标空间

2. 单射的视角（从源空间看）：

   • 核心问题：源空间中不同的元素是否保持不同？
   • 单射条件：源空间中的不同元素映射到目标空间中的不同元素
   • 不关心：目标空间中可能有元素没被映射到
   • 线性代数中：变换没有"压缩"或"折叠"维度，没有信息丢失

3. 双射的视角（同时关注两个空间）：

   • 核心问题：是否存在完美的一一对应关系？
   • 双射条件：既是满射又是单射
   • 要求：每个源元素恰好映射到一个目标元素，每个目标元素恰好被一个源元素映射
   • 线性代数中：变换前后的空间维数相同，且没有信息丢失或重叠

实际应用中的比喻

1. 满射：像是分配工作任务

   • 每项任务都必须有人负责（每个目标元素都被映射到）
   • 允许一个人负责多项任务（多对一映射）
   • 关键是不能有任务无人认领

2. 单射：像是分配独特的工号

   • 每个员工都有唯一的工号（不同源元素映射到不同目标元素）
   • 可能有一些工号未分配（目标空间可能未被完全覆盖）
   • 关键是不能有两个员工共享同一个工号

3. 双射：像是完美的一对一约会配对

   • 每个人都恰好有一个约会对象（一一对应）
   • 没有人被落单，也没有人约会多个对象
   • 必须要求参与者人数相等

你现在对源空间、目标空间以及满射和双射的不同角度有更清晰的理解了吗？