机器学习系列 【一】逻辑回归算法

内容说明

      本文主要讲解Logistic算法的数学原理、优化方法以及python代码实现，可供机器学习爱好者借鉴学习。文中所给出的python代码，来自于2020年华为软件精英挑战赛官方给出的LR算法源码，读者也可借助本文快速读懂大赛示例代码。

一、Logistic回归算法基本原理

      Logistic 回归是二分类任务中最常用的机器学习算法之一。它的设计思路简单，易于实现，可以用作性能基准，且在很多任务中都表现很好。其优点是计算代价不高，易于理解和实现；其缺点是容易欠拟合，分类精度可能不高。
在逻辑回归算法中，利用了Logistic函数（或称Signoid函数），在该函数中自变量的取值范围为(-INF,INF)，函数值域为(0，1)。其表达式为：

由于sigmoid函数的定义域是(-INF, +INF),而值域为(0, 1)。因此最基本的LR分类器适合于对两分类（类0，类1）目标进行分类。Sigmoid 函数是个很漂亮的“S”形，如下图所示：
      LR分类器(Logistic Regression Classifier)目的就是从训练数据特征学习出一个0/1分类模型–这个模型以样本特征的线性组合${\sum }_{i=1}^n{\theta }_i{x}_i$作为自变量，使用logistic函数将自变量映射到(0,1)上。因此LR分类器的求解就是求解一组权值${\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4...{\theta }_n$（其中${\theta }_0$是名义变量–dummy，为常数，实际工程中常另$x_0=1.0$。不管常数项有没有意义，最好保留），并代入Logistic函数构造出一个预测函数：

      函数的值表示结果为1的概率，就是特征属于y=1的概率。因此对于输入x分类结果为类别1和类别0的概率分别为：

      当我们要判别一个新来的特征属于哪个类时，按照下式求出一个z值：

      式中，$x_1,x_2,x_3....,x_n$为样本数据在各个维度的特征，n是维数。
      将上式结果带入Signoid函数中，即得到$g({\theta }^{T}x)$。若该值大于0.5，则认为样本x属于$y=1$的类，反之则属于$y=0$的类，这就是逻辑回归算法的分类依据。（注意，这里假设统计样本是均匀分布的，所以设阈值为0.5）。
      对逻辑回归算法的学习，核心就在求解权值${\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4...{\theta }_n$上。具体求解，涉及到了极大似然估计E和优化算法的概念，数学中最优化算法常用的就是梯度上升（下降）算法。下文将详细介绍权值求解过程。

二、Logistic回归数学推导

（1）梯度下降法求解

      假设有n个观测样本，观测值分别为$y_1,y_2...,y_n$设$p_i=p(y_i=1|x_i)$为给定条件下得到$y_i=1$的概率。在同样的条件下，$y_i=0$的条件概率为$p(y_i=0|x_i)=1-p_i$。于是，得到一个观测值的概率为：

      （该式含义为，当y取1时，1-y=0，故上式可化为$p(y=1|x;\theta )=(h_{\theta }(x))$；当当y取10时，1-y=1，故上式可化为$p(y=10|x;\theta )=(1-h_{\theta }(x))$）

因为各项观测独立，所以它们的联合分布可以表示为各边际分布的乘积：

      (其中，m为统计样本数目)

      该式称为n个观测的似然函数。我们的目标是能够求出使这一似然函数的值最大的参数估计。于是，最大似然估计的关键就是求出参数${\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4...{\theta }_n$，使上式取得最大值。
为了方便求导，对上式取对数：

      最大似然估计就是求使上式取最大值时的$\theta$，这里可以使用梯度上升法求解，求得的$\theta$就是要求的最佳参数。将$J(\theta )$取为：$J(\theta )=-(1/m)l(\theta )，J(\theta )$最小值时的$\theta$则为要求的最佳参数。通过梯度下降法求最小值。$\theta$的初始值可以全部为1.0，更新过程为：

      （其中，j表样本第j个属性，共n个；$\alpha$表示步长–每次移动量大小，可自由指定）

其中:$$\frac{\partial g({\theta }^T{x}_i)}{\partial {\theta }_j}=\frac{\partial }{\partial {\theta }_j}(\frac{1}{1+e^{-}{\theta }^{T}x})=g({\theta }^T{x}_i)(1-g({\theta }^T{x}_i))\frac{\partial }{\partial {\theta }_j}{\theta }^T{x}_i$$
因此，$\theta$（可以设初始值全部为1.0）的更新过程可以写成：

      （i表示第i个统计样本，j表样本第j个属性；$a$表示步长）
      该公式将一直被迭代执行，直至达到收敛。（$J(\theta )$在每一步迭代中都减小，如果某一步减少的值少于某个很小的值$ϵ$(小于0.001)，则其判定收敛）或某个停止条件为止（比如迭代次数达到某个指定值或算法达到某个可以允许的误差范围）。

（2）向量化Vectorization求解

      Vectorization是使用矩阵计算来代替for循环，以简化计算过程，提高效率。如上式，Σ(…)是一个求和的过程，显然需要一个for语句循环m次，所以根本没有完全的实现vectorization。下面介绍向量化的过程：约定训练数据的矩阵形式如下，x的每一行为一条训练样本，而每一列为不同的特称取值：

      $g(A)$的参数$A$为一列向量，所以实现g函数时要支持列向量作为参数，并返回列向量。由上式可知$h\theta (x)-y$可由$g(A)-y$直接计算求得。

θ更新过程可以改为：

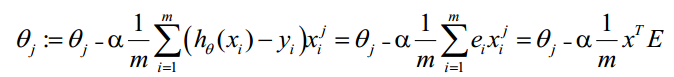
      综上所述，Vectorization后θ更新的步骤如下：

      （1）求$A=X\ast \theta$(此处为矩阵乘法，$X$是$（m,n+1）$维向量，$\theta$是$(n+1，1)$维列向量，$A$就是$(m,1)$维向量)

      （2）求$E=g(A)-y$$(E、y$是$(m,1)$维列向量)

      （3）求$\theta :=\theta -\alpha x^{T}E$ （a表示步长）

（3）步长$\alpha$的选取

      在递推公式中，$\alpha$是调整步长，它的实质是梯度下降法中，每一步向当前负梯度方向调整的大小因子，也就是分类器学习到最优权向量的速度。因此，当我们在线性分类器的学习过程中使用梯度下降法时，调整步长$\alpha$也称为“学习速率”。$\alpha$的取值越大，求解的速度越快，但求解路径越不光滑，求解的精度越差，容易过冲甚至振荡； $\alpha$的取值越小，求解的速度越慢，但求解精度越高。因此，只要使用梯度下降法来训练分类器，其求解精度和速度之间是存在矛盾的。通常步长的选取，使用较多的两种方法为：固定步长和变步长法。

1、固定步长
      即令$\alpha$取某一固定正值，选取之后测试$\alpha$取该值时，分类器的训练效果，再根据训练效果来决定是否调整步长值。如果迭代不能正常进行（J增大了，步长太大，迈过了碗底）则考虑使用更小的步长，如果收敛较慢则考虑增大步长。每次选取的$\alpha$值，约取为前一次的3倍。总的来说，$\alpha$的选定需要凭借一定的经验以及反复尝试方能找到合适的步长。\alpha$取值示例如：…, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1…。

2、变步长法
      变步长法的思路很符合我们通常的认识，即在优化过程中，刚开始迭代时，训练效果与目标相差较大，“还有很长一段路需要走”，故此时可增大$\alpha$值，改进优化速度。当优化接近目标值时，参数的更新就需要小心谨慎了。如果步长选取太大，很容易一步跨过目标值，导致算法无法收敛。因此，在训练过程中，可以取按照某种规律逐步减少的$\alpha$，使得算法开始时收敛较快，接近最优解时收敛速度变慢，以提高求解的精度。比较常用的变步长法是取：$$\alpha (k+1)=\lambda \frac{1}{k}$$       其中，$\lambda$是选取的较大初始步长，k为迭代次数。

三、Logistic回归算法python实现

      本文给出的程序不可直接运行，代码的意义是为了帮助学习者了解逻辑回归算法的实现原理。使读者不通过机器学习算法库，也可以自己手写机器学习算法。介绍之前，先上代码：

class LR:
    def __init__(self, train_file_name, test_file_name, predict_result_file_name):
        self.train_file = train_file_name     # 训练集地址
        self.predict_file = test_file_name    # 测试集地址
        self.predict_result_file = predict_result_file_name   # 测试结果保存地址
        self.max_iters = 5000                 
        self.rate = 0.1  
        self.feats = []                       # 存放训练数据的空列表
        self.labels = []                      # 存放样本标签的空列表
        self.feats_test = []                  # 存放测试数据的空列表
        self.labels_predict = []              # 存放预测结果的空列表
        self.param_num = 0                    # 数据维度
        self.weight = []                      

    def loadDataSet(self, file_name, label_existed_flag):
        feats = []
        labels = []
        fr = open(file_name)
        lines = fr.readlines()
        for line in lines:
            temp = []
            allInfo = line.strip().split(',')
            dims = len(allInfo)
            if label_existed_flag == 1:
                for index in range(dims-1):
                    temp.append(float(allInfo[index]))
                feats.append(temp)
                labels.append(float(allInfo[dims-1]))
            else:
                for index in range(dims):
                    temp.append(float(allInfo[index]))
                feats.append(temp)
        fr.close()
        feats = np.array(feats)
        labels = np.array(labels)
        return feats, labels

    def loadTrainData(self):
        self.feats, self.labels = self.loadDataSet(self.train_file, 1)

    def loadTestData(self):
        self.feats_test, self.labels_predict = self.loadDataSet(
            self.predict_file, 0)

    def savePredictResult(self):
        print(self.labels_predict)
        f = open(self.predict_result_file, 'w')
        for i in range(len(self.labels_predict)):
            f.write(str(self.labels_predict[i])+"\n")
        f.close()

    def sigmod(self, x):
        return 1/(1+np.exp(-x))

    def printInfo(self):
        print(self.train_file)
        print(self.predict_file)
        print(self.predict_result_file)
        print(self.feats)
        print(self.labels)
        print(self.feats_test)
        print(self.labels_predict)

    def initParams(self):
        self.weight = np.ones((self.param_num,), dtype=np.float)

    def compute(self, recNum, param_num, feats, w):
        return self.sigmod(np.dot(feats, w))

    def error_rate(self, recNum, label, preval):
        return np.power(label - preval, 2).sum()

    def predict(self):
        self.loadTestData()
        preval = self.compute(len(self.feats_test),
                              self.param_num, self.feats_test, self.weight)
        self.labels_predict = (preval+0.5).astype(np.int)
        self.savePredictResult()

    def train(self):
        self.loadTrainData()
        recNum = len(self.feats)
        self.param_num = len(self.feats[0])
        self.initParams()
        ISOTIMEFORMAT = '%Y-%m-%d %H:%M:%S,f'
        for i in range(self.max_iters):
            preval = self.compute(recNum, self.param_num,
                                  self.feats, self.weight)
            sum_err = self.error_rate(recNum, self.labels, preval)
            if i%30 == 0:
                print("Iters:" + str(i) + " error:" + str(sum_err))
                theTime = datetime.datetime.now().strftime(ISOTIMEFORMAT)
                print(theTime)
            err = preval - self.labels
            delt_w = np.dot(self.feats.T, err)
            delt_w /= recNum
            self.weight -= self.rate*delt_w

      文中给出的，是逻辑回归算法完整的一个类。类中主要包括几个部分：变量的初始化、数据集的加载和预处理、预测结果的保存、Signoid函数定义以及具体的训练过程。下面对重点内容进行介绍：

（1）数据集加载

      在类中，首先构建了一个loadDataSet函数，通过该函数，可将给定的由逗号分隔开的txt格式数据文档，转化为数据，存放到预先初始化的列表中。代码中：allInfo = line.strip().split(’,’) 作用是对文档中的每一行数据，按“，”将每个数据提取出，按列存放到列表中。语句：if label_existed_flag == 1:是对训练集和测试集的一个判断，在后期调用loadDataSet函数，处理训练集文档时，令$label_existed_flag == 1；处理测试集文档时，令label_existed_flag = = 1。如此编写是因为训练数据与测试数据的差异性，在训练数据中，文档最后一列存放的是数据标签，数据标签也需要提取出来存放到列表中。而对测试数据而言，最后一列并非标签。因此对两个文档的处理方法，略有差别。故通过01判断，选择适合各自的处理方法。最后，对训练数据文档和测试数据文档，分别调用loadDataSet函数，将训练数据及标签存放在：self.feats和self.labels中。将测试数据存放在：self.feats_test中。

（2）模型训练

      在得到处理后的训练数据及标签之后，可以开始训练过程中。训练过程主要是对系列权值${\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4...{\theta }_n$的不断迭代更新，使用的优化方法为梯度下降法。在前面的数学推导中，我们得到了算法的迭代公式为：

      但考虑到倘若使用该式进行更新权值，不可避免的会使用到for循环语句，使用算法效率极低。为了提高算法效率，我们改用了向量化Vectorization求解的方法更新权值，迭代公式为：

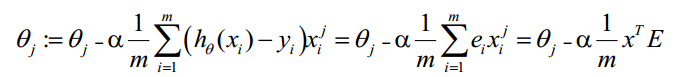
在算法中的具体实现代码为：

 err = preval - self.labels
 delt_w = np.dot(self.feats.T, err)
 delt_w /= recNum
 self.weight = self.weight-self.rate*delt_w

      其中，算法中的$np.dot(self.feats.T,err)$即对应公式中的：$x^{T}E$，$recNum$即为公式中的m。
      第一期博客到这里就结束了，文中不当之处还请各位读者批评指正。如果还有不太理解的地方，可在评论区留言。