第二章姿态解算以及Mahony互补滤波算法

心里种下一颗种子达拉崩吧啦

已于 2024-07-01 20:01:53 修改

阅读量810

点赞数 17

分类专栏：四轴飞行器项目记录文章标签：算法 c语言

于 2024-07-01 15:09:14 首次发布

本文链接：https://blog.csdn.net/weixin_44745712/article/details/140084791

版权

四轴飞行器项目记录专栏收录该内容

3 篇文章 0 订阅

订阅专栏

四轴控制算法（PID、Mahony互补滤波算法等）

第二章姿态解算以及Mahony互补滤波算法

文章目录

四轴控制算法（PID、Mahony互补滤波算法等）
前言
一、姿态解算是什么？
二、姿态解算常用名词
三、Mahony互补滤波算法
总结

前言

第一章获取了MPU9250的原始数据，这一章节将对这些原始数据进行数据融合，获取飞行器机体坐标系在地球坐标系中的姿态角(也就是欧拉角)，通过 Mahony 互补滤波算法解算出姿态角，所以姿态解算的基础就是 IMU 数据。

一、姿态解算是什么？

姿态解算也叫做姿态分析，姿态估计，姿态融合。姿态解算是根据 IMU(惯性测量单元)数据(陀螺仪、加速度计、罗盘等)求解出飞行器的空中姿态，所以也叫做 IMU 数据融合。

二、姿态解算常用名词

1.坐标系

导航坐标系:（图左）在多旋翼中，又叫地球坐标系、地理坐标系。通常，采用北东地(NED)构成坐标系的 X,Y,Z 轴。

机体坐标系:（图右）固联在多旋翼飞行器上，坐标系原点定位于飞行器中心点(假设中心点与重心点重合)，X轴指向机头方向，Y轴指向机头的右方，Z轴垂直于 X，Y轴构成平面垂直向下，这个可以用“右手定则”确定坐标轴的正方向。

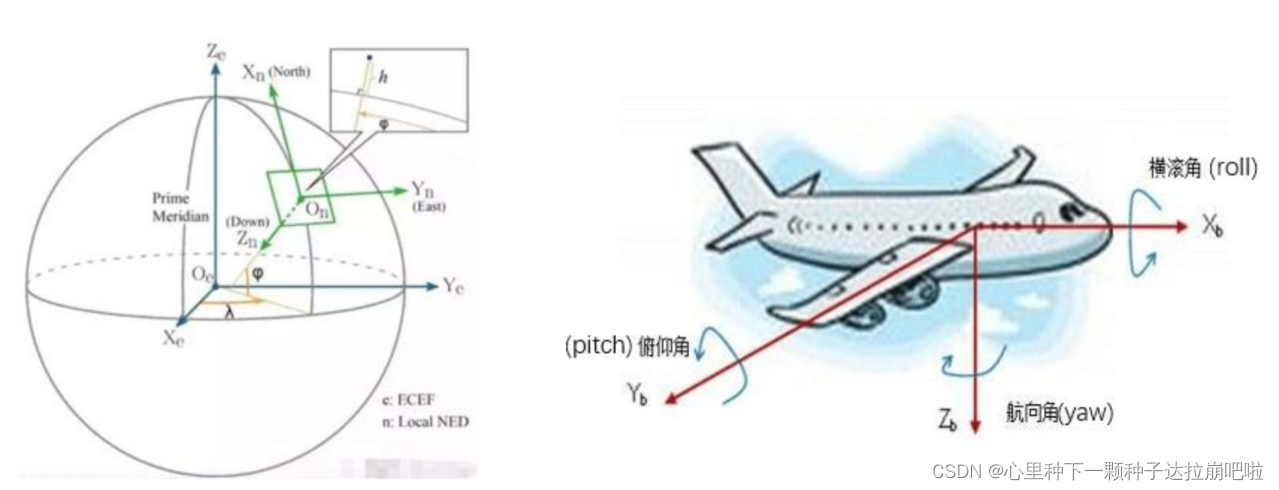
在这里插入图片描述

2.什么是姿态

姿态通俗的说就是指我们站在地面上观察**飞行器的俯仰(pitch)/横滚(ro11)/航向(yaw)**状态。飞行器需要实时知道当前自己的姿态，才能够根据需要操控其接下来的动作，例如保持平稳，翻滚。

数学模型:姿态是用来描述一个刚体的固连坐标系和参考坐标系之间的角位置关系(姿态角),有一些数学表示方法。很常见的就是欧拉角,四元数,矩阵，轴角。

飞行器姿态描述套用上面的数学模型，参考坐标系就对应着导航坐标系是固定不变的。我们通常用坐标系R表示。固连坐标系就对应着机体坐标系，用坐标系r表示。那么我们就可以用欧拉角，四元数等数学方法来描述r与R的角位置关系。这就是飞行器姿态解算的数学模型。

3.姿态表示方法

姿态有多种数学表示方式，常见的是四元数，欧拉角，方向余弦矩阵。他们各自有其自身的优点，在不同的领域使用不同的表示方式。在四轴飞行器中通常使用的是四元数、欧拉角和方向余弦矩阵。
飞机姿态角是按欧拉概念定义的，故亦称欧拉角。飞机姿态角是由机体坐标系与地理坐标系之间的关系确定的，用航向角、俯仰角和横滚角三个欧拉角表示。不同的转动顺序会形成不同的坐标变换矩阵，通常按航向角、俯仰角和横滚角的顺序来表示机体坐标系相对地理坐标系的空间转动。

–

1）欧拉角表示:

莱昂哈德·欧拉用欧拉角来描述刚体在三维欧几里得空间的取向。对于在三维空间里的一个参考系，任何坐标系的取向，都可以用三个欧拉角来表现。参考系又称为实验室参考系，是静止不动的。而坐标系则固联于刚体随着刚体的旋转而旋转。如下图的左数第一个图a、8、Y就是欧拉角。后面紧跟的三个图演示了欧拉角是如何产生的，分别对应哪个角度。
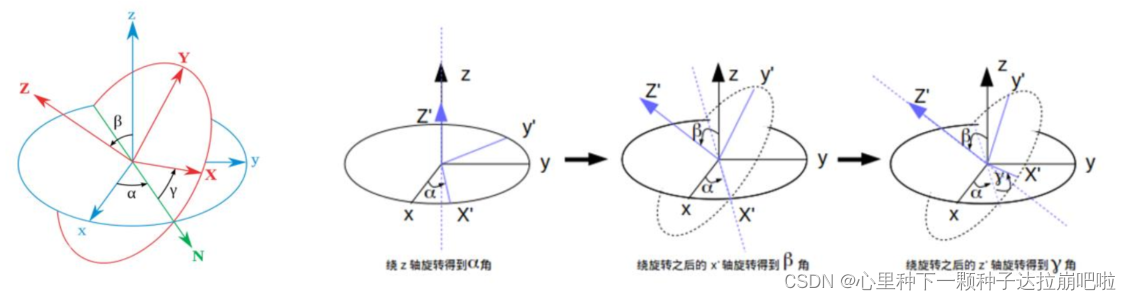
在这里插入图片描述

–

2）四元数表示：

四元数是由爱尔兰数学家威廉·卢云·哈密顿在1843年发现的数学概念。从明确的角度而言，四元数是复数的不可交换延伸。

如把四元数的集合考虑成多维实数空间的话，四元数就代表着一个四维空间，相对于复数为二维空间。
在这里插入图片描述

4.姿态解算的目的

姿态解算目的获取飞行器机体坐标系在地球坐标系中的姿态角(也就是欧拉角)，但是欧拉角不是直接测量的而是通过 IMU(惯性测量单元)数据(陀螺仪、加速度计、罗盘等)通过 Mahony 互补滤波算法解算出姿态角，所以姿态解算的基础就是 IMU 数据，这也是为什么将获取MPU9250的原始数据作为第一章的原因。

三、Mahony互补滤波算法

1.四元数、欧拉角、方向余弦矩阵在姿态解算中的使用

姿态角是由旋转产生的,一般旋转有4种表示方式:方向余弦矩阵表示、欧拉角表示、轴角表示、四元数表示。其中方向余弦矩阵表示适合变换向量，欧拉角最直观，轴角表示适合几何推导，而在组合旋转方面，四元数表示最佳。因为姿态解算需要频繁组合旋转和用旋转变换向量。

所以我们使用四元数来保存飞行器的姿态(也就是飞机在地球坐标系中的俯仰/横滚/航向状态)。姿态控制算法的输入参数必须要是欧拉角。所以在需要控制的时候，会将四元数转化为欧拉角，但是四元数转化成欧拉角又需要借助方向余弦阵来实现。
姿态解算到姿态控制的整个流程。MPU9250输出的3个维度的陀螺仪值、3 个维度的加速度值、3个维度的磁力计值，每个值为16位精度。MPU9250输出的 AD 值通过姿态解算算法得到飞行器当前的姿态(姿态使用四元数表示)，然后将四元数转化为欧拉角，用于姿态控制算法(PID控制)中。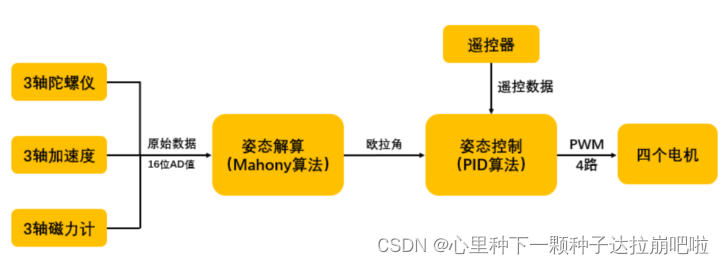在这里插入图片描述

2.分析Mahony互补滤波算法

1）欧拉角描述的方向余弦矩阵

定理：空间中坐标系的任意旋转，等效于依次绕三个坐标轴的定轴旋转。
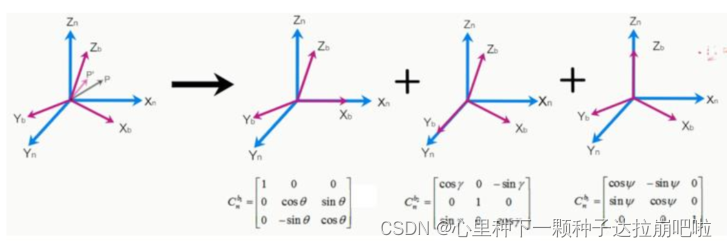
在这里插入图片描述
如上图所示紫色的坐标系记为b系，蓝色的坐标系记为n系。b系是由n系任意旋转得到。那么这个旋转等效于绕 Xn 轴旋转，绕 Yn 轴旋转，绕 Zn 轴旋转的叠加。但是这种旋转怎么表示呢?换句话说p点旋转到p’他们的坐标有什么对应关系呢?
（具体求出三个旋转阵的过程不再详解）

没错，由三个旋转阵组成的方向余弦矩阵Cn-b就可以描述b系相对于n系的旋转，如果我们知道任意向量在b系中的坐标，那么就可以利用方向余弦矩阵求出它在n系中的坐标，反之亦然。
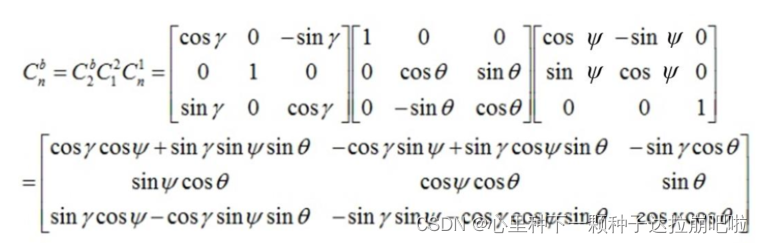
在这里插入图片描述

这个方向余弦矩阵还有一个特点就是这个矩阵的元素都是由欧拉角的正弦和余弦组合成的，而我们需要的姿态也就是这三个角，那么我们该怎么求出欧拉角呢? 那我们只需套用欧拉角的微分方程就可以解出这三个角，但是由于欧拉角微分方程中包含了大量的三角运算，这给实时解算带来了一定的困难。而且当俯仰角为 90 度时方程式会出现神奇的“死锁”。所以欧拉角方法只适用于水平姿态变化不大的情况，而不适用于全姿态飞行器的姿态确定。

–
我们将该方向余弦矩阵记作：
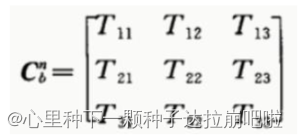
在这里插入图片描述

也就是说矩阵 Cb->n可以将b系的向量转换到n系表示，矩阵 Cn->b可以将n系的向量转换到b系表示。那么可以根据矩阵中T32、T31、T12、T22的值就可以求出需要的三个欧拉角：

2）四元数描述的方向余弦矩阵

既然欧拉角能描述方向余弦矩阵，那么我们是否也能用四元数来描述方向余弦矩阵呢?
那是肯定的！！！
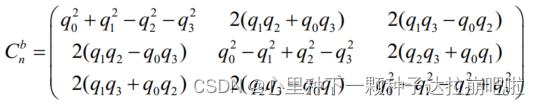
在这里插入图片描述
既然 Cn->b。方向余弦矩阵中的元素，都已经被四元数的四个变量给替换掉了。
那么我们求解姿态的问题就转化成了求解这一组四元数的问题了。

一旦求解出 q0,q1,q2,93,也就能反解出欧拉角了。注意不同的绕定轴的旋转顺序就对应不同的反解欧拉角的公式(例如绕 Z->Y->X 和 Z->X>Y 得到的欧拉角描述旋转矩阵是不相同的)。所以说上面的四元数转欧拉角的公式不是唯一的。本次讲解是按 Z->X>Y 的旋转顺序为例进行的讲解。

3）求解四元数

通过前面的分析，一组四元数已经足够表达一个飞行器的完整姿态了，因为通过四元数可以构建出一个方向余弦矩阵，而方向余弦矩阵正是由于飞行器在空间中发生旋转所引起的，因此我们也就可以说一组四元数就包含了一个完整的旋转过程，也就我们说的飞行姿态。那么我们想要得到飞行姿态，只需要实时更新四元数就行了。

那么我们就可以构建四元数关于时间的微分方程，来研究四元数的变化过程因为考虑到陀螺仪测量的角速度，所以我们用四元数的三角表示式来建立一个微分方程，如果可以求解出该微分方程，那么也就成功的解出了四元数。

四元数的三角表达式：
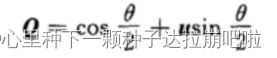
在这里插入图片描述
令四元数对时间t进行微分，可得到微分方程化简后如下:

记为：
接下来就剩下求解这个微分方程了，但是求解这个微分方程，还需要考虑单片机只能处理离散数据的特点。因此选择一阶龙格库塔法来求解微分方程，一阶龙格库塔法可以通过有限次迭代求解出函数的微分方程的解。
设有微分方程：
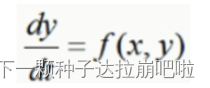
在这里插入图片描述
根据一阶龙格库塔法可以求解y的迭代公式：

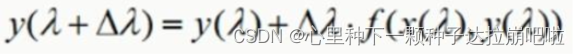
套用公式可得四元数微分方程：

写成矩阵形式如下：

观察上面的公式:[q0q1q2q3]t+▲t 是当前四元数，[q0q1q2q3]t是上个周期的四元数，▲t 是计算周期，最后这个矩阵里的元素是各轴角速度(Wx,Wy,Wz)与四元数(q0,q1,q2,q3)的组合。角速度(Wx,Wy,Wz)数据是可以通过陀螺仪测出来的，如果陀螺仪的数据是理想状态，那么我们就可以求出准确的四元数。但是事与愿违由于噪声的影响会引入误差，因此我们需要使用加速度计和磁力计对陀螺仪数据进行校准。所以说我们在套用上面公式求解四元数时，一定要先保证陀螺仪数据的可靠性。

4）传感器数据融合

陀螺仪，测量角速度，具有高动态特性，它是一个间接测量角度的器件。它测量的是角速度，要将角速度对时间积分才能得到角度。由于噪声等误差影响，在积分作用下不断积累，最终导致陀螺仪的低频干扰和漂移。
假设陀螺仪固定不动，理想角速度值是 0dps(degree per second)，但是有一个偏置 0.1dps 加在上面，于是测量出来是 0.1dps，积分一秒之后，得到的角度是 0.1度，1分钟之后是6度，还能忍受，一小时之后是 360 度，转了一圈，也就是说，陀螺仪在短时间内有很大的参考价值。使用陀螺仪获得角度，一定要考虑积分误差的问题。

–
加速度计，测量当前加速度(包含重力加速度 g)的方向(也叫重力感应器)，在悬停时，输出为g。由其测量原理导致的高频信号敏感，使得加速度计在振动环境中高频干扰较大。
加速度计若是绕着重力加速度的轴转动,则测量值不会改变,也就是说无法感知这种水平旋转。
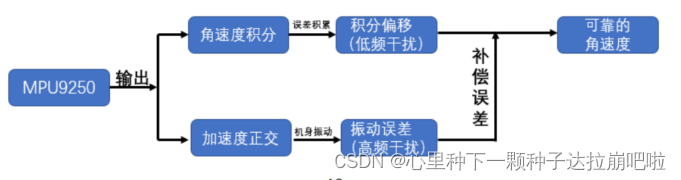
在这里插入图片描述
上面解四元数微分方程的公式里，直接用到了角速度数据，所以我们需要尽可能减小陀螺仪的积分误差，我们数据融合的思路是用加速度数据来校准陀螺仪数据的积分误差。那么我们该怎么让陀螺仪数据与加速度数据建立关系呢?
这时候我们就需要用方向余弦阵了:
在这里插入图片描述
设在导航坐标系(n系)下有重力加速度向量gn，把gn旋转到机体坐标系(b系)，得到其机体坐标系的重力加速度向量vb,则两者的转换关系可以用方向余弦矩阵Cn->b来实现转换如下:

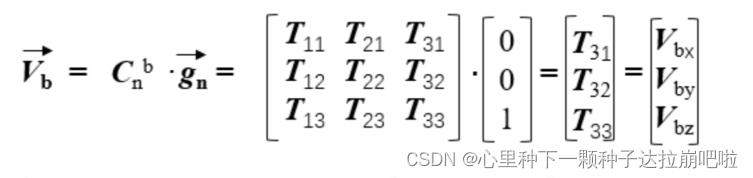
观察上计算结果我们可以发现vb=[T31 T32 T33]^T,我们发现转换到 b系下的vb恰好是方向余弦矩阵Cn->b的第三列，并且第三列是用四元数进行表示的，也就是说四元数和机体的重力加速度是可以相互推导的，并且四元数又是用角速度数据求出来的。那么关系如下:
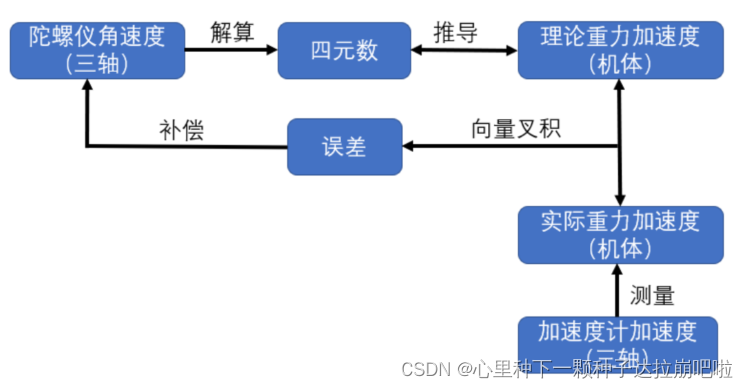
在这里插入图片描述
由图可知四元数和理论重力加速度(vb)可以相互推导得出，理论上四元数推出来的 (vb)应该和加速度计测量的实际重力加速度(ab)完全重合,量)，但是由于四元数是由角速度数据解算出来的，由于角速度数据有误差，导致了 vb和 ab不再重合，那么我们此时就可以通过向量的叉积(外积)，来度量这个误差的大小。
（关于叉积补偿角速度后期会单独一篇讲解，挖个坑~）

5）滤波算法之误差补偿

上面已经利用向量的叉积度量了vb和 ab的误差 error;那么这个 error 该如何补偿到陀螺仪数据上呢?
我们这里需要借助 PID 控制思想，用 PI(比例-积分)控制器来控制补偿值的大小，PI控制器公式如下:

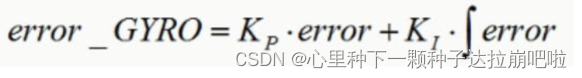
在这里插入图片描述
利用比例项来控制传感器的可信度,其中Kp越大就越相信加速度计，Kp越小就越相信陀螺仪，积分项来消除静态误差。
把 PI控制器计算出来的补偿值加在角速度上，既可得到可信度较高的陀螺仪数据，然后再带入到一阶龙格库塔法公式里就可以得到当前的四元数。
在这里插入图片描述

代码程序：

#define Acc_Gain 0.0001220f			//加速度转换单位(初始化加速度计量程+-4g，由于mpu6050的数据寄存器是16位的，LSBa = 2*4 / 65535.0)
#define Gyro_Gain 0.0609756f		//角速度转换为角度(LSBg = 2000*2 / 65535)
#define Gyro_Gr 0.0010641f			//角速度转换成弧度(3.1415 / 180 * LSBg)
#define G 9.80665f					// m/s^2

extern short ax,ay,az;
extern short gx,gy,gz;


static float invSqrt(float x) 		//快速计算 1/Sqrt(x)
{
	float halfx = 0.5f * x;
	float y = x;
	long i = *(long*)&y;
	i = 0x5f3759df - (i>>1);
	y = *(float*)&i;
	y = y * (1.5f - (halfx * y * y));
	return y;
}


void Prepare_Data(void)
{
	MPU_Get_Accelerometer(&ax,&ay,&az);			//获取加速度计原始值
	MPU_Get_Gyroscope(&gx,&gy,&gz);				//获取角速度原始值
	
	//将加速度原始AD值转换为m/s^2
	ax = (float)ax * Acc_Gain * G;
	ay = (float)ay * Acc_Gain * G;
	az = (float)az * Acc_Gain * G;
	
	//将陀螺仪AD值转换为 弧度/s
	gx = (float)gx * Gyro_Gr;
	gy = (float)gy * Gyro_Gr;
	gz = (float)gz * Gyro_Gr;
}



#define Kp 1.50f
#define Ki 0.005f
#define halfT 0.0025f						//计算周期的一半，单位s

extern float Yaw,Pitch,Roll;				//我要给其他文件用所以定义了extern，不用管
float q0 = 1, q1 = 0, q2 = 0, q3 = 0;		//四元数
float exInt = 0, eyInt = 0, ezInt = 0;		//叉积计算误差的累计积分


void Imu_Update(float gx,float gy,float gz,float ax,float ay,float az)
{
	u8 i;
	float vx,vy,vz;							//实际重力加速度
	float ex,ey,ez;							//叉积计算的误差
	float norm;
	
 	float q0q0 = q0*q0;
 	float q0q1 = q0*q1;
	float q0q2 = q0*q2;
	float q0q3 = q0*q3;
	float q1q1 = q1*q1;
 	float q1q2 = q1*q2;
 	float q1q3 = q1*q3;
	float q2q2 = q2*q2;
	float q2q3 = q2*q3;
	float q3q3 = q3*q3;
	
	if(ax*ay*az == 0)
		return;
	
	//加速度计测量的重力方向(机体坐标系)
	norm = invSqrt(ax*ax + ay*ay + az*az);			//之前这里写成invSqrt(ax*ax + ay+ay + az*az)是错误的，现在修改过来了
	ax = ax * norm;
	ay = ay * norm;
	az = az * norm;
	
	//四元数推出的实际重力方向(机体坐标系)
	vx = 2*(q1q3 - q0q2);												
  	vy = 2*(q0q1 + q2q3);
  	vz = q0q0 - q1q1 - q2q2 + q3q3;
	
	//叉积误差
	ex = (ay*vz - az*vy);
	ey = (az*vx - ax*vz);
	ez = (ax*vy - ay*vx);
	
	//叉积误差积分为角速度
	exInt = exInt + ex * Ki;
	eyInt = eyInt + ey * Ki;
	ezInt = ezInt + ez * Ki;
	
	//角速度补偿
	gx = gx + Kp*ex + exInt;
	gy = gy + Kp*ey + eyInt;
	gz = gz + Kp*ez + ezInt;
	
	//更新四元数
  	q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT;
  	q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT;
  	q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT;
  	q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT;	
	
	//单位化四元数
  	norm = invSqrt(q0*q0 + q1*q1 + q2*q2 + q3*q3);
  	q0 = q0 * norm;
  	q1 = q1 * norm;
  	q2 = q2 * norm;  
  	q3 = q3 * norm;
	
	//四元数反解欧拉角
	Yaw = atan2(2.f * (q1q2 + q0q3), q0q0 + q1q1 - q2q2 - q3q3)* 57.3f;
	Pitch = -asin(2.f * (q1q3 - q0q2))* 57.3f;
	Roll = atan2(2.f * q2q3 + 2.f * q0q1, q0q0 - q1q1 - q2q2 + q3q3)* 57.3f;
}
————————————————

总结

以上就是要讲的内容，如有理解和讲解错误的地方请在评论区指正。

心里种下一颗种子达拉崩吧啦

关注

17
点赞
踩
24

收藏

觉得还不错? 一键收藏
0
评论
第二章姿态解算以及Mahony互补滤波算法

第一章获取了MPU9250的原始数据，这一章节将对这些原始数据进行数据融合，获取飞行器机体坐标系在地球坐标系中的姿态角(也就是欧拉角)，通过Mahony 互补滤波算法解算出姿态角，所以姿态解算的基础就是 IMU 数据。姿态通俗的说就是指我们站在地面上观察**飞行器的俯仰(pitch)/横滚(ro11)/航向(yaw)**状态。飞行器需要实时知道当前自己的姿态，才能够根据需要操控其接下来的动作，例如保持平稳，翻滚。数学模型。
复制链接

扫一扫