机器学习(周志华) 参考答案 第一章 绪论 1.2 一个不错的解法想法

机器学习(周志华) 参考答案 第一章 绪论 1.2

       这回带来的是西瓜书1.2的更加精简的算法，core i7 八核一秒算完，理论上应该是极为简便的了。

2.与使用单个合取式来进行假设表示相比，使用“析合范式”将使得假设空间具有更强的表示能力。若使用最多包含k个合取式的析合范式来表达1.1的西瓜分类问题的假设空间，试估算有多少种可能的假设。

       这时候我们来思考一下，西瓜书上的冗余其实就是不能有领域的重复覆盖。这时候比起遍历算法，我们可以想另外一种匹配算法：
       我们有一个2 $\times$ 3 $\times$ 3 的魔方，即（青绿 乌黑）（蜷缩 硬挺 稍蜷） （浊响 沉闷 清脆）的全部配对，那么问题转化为，我们找出全部的方法，使我们在每一个方块中填色一直填满而且不会填两次。
       我们一次可以填一个、一行、一列、一竖列或者一面或者一次一整个。这些都是可以用合取式来表示的，所以问题浅显不？

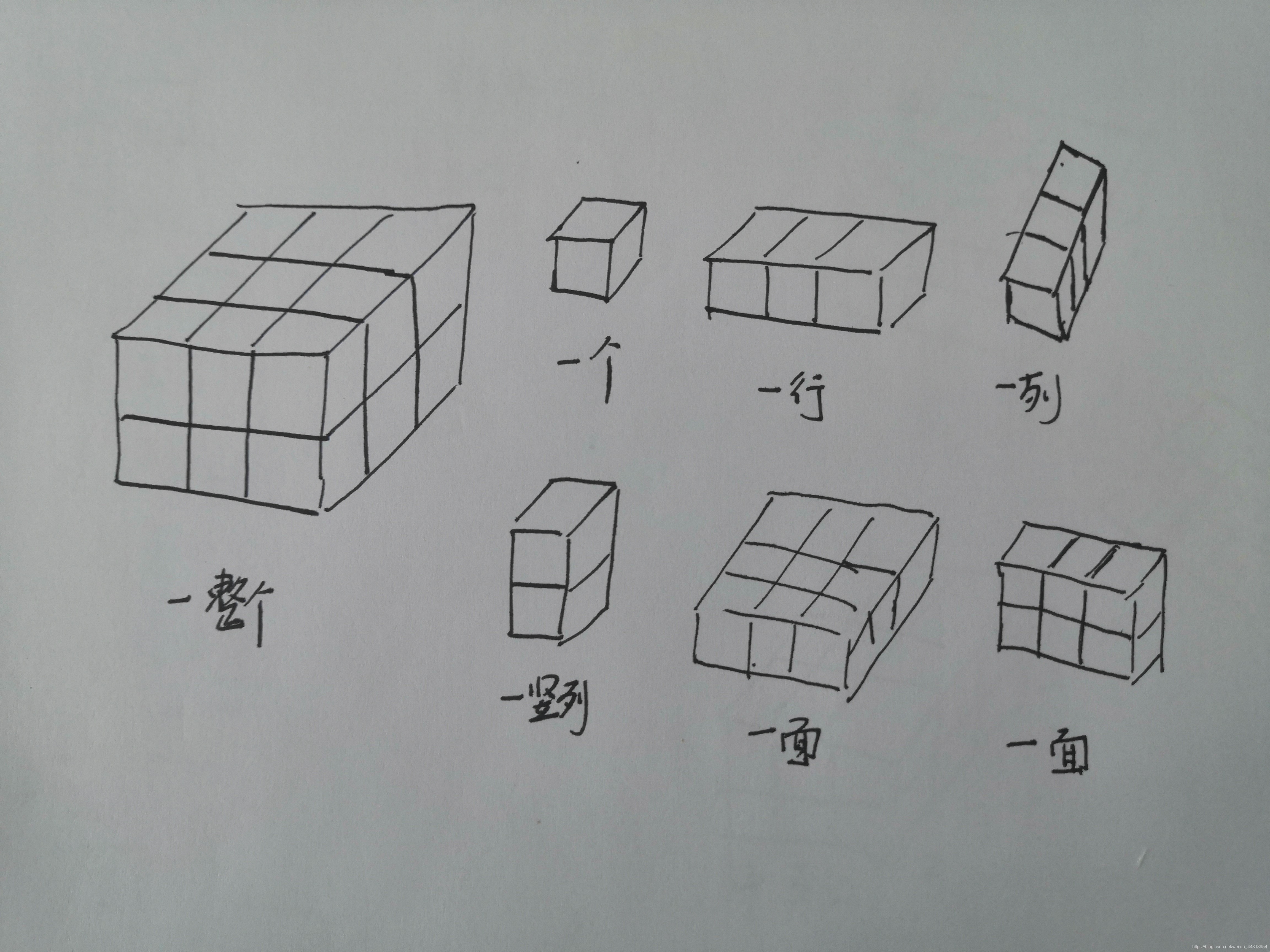
       我们最终的目的无非就是把这个魔方填满，找出全部的方法。只需要首先找出全部符合条件的填色方法，之后先假设我们要使用第一种填色方式，试图找出一个填法最复杂的（因为举个例子，乌黑 蜷缩 *其实是由乌黑蜷缩浊响、乌黑蜷缩沉闷、乌黑蜷缩清脆三个构成的）如果我们找到一个最长的填色路径，可以很容易得出比它简单的那些结果。
       仔细地解释一下最复杂，意思就是以某个填色方法填入第一次，之后将魔方填满的最长路径。比这个魔方简化但是也能填满的路径可以直接用肉眼判断出来。

此时问题变得很简单，我们只需要递归就可以了。
我们使用的是matlab，如果用其他程序也一样。
首先上函数：

第一个函数addlist的作用是，收入一个空的魔方（即2