一文掌握复杂网络的基础知识点

一、简介

互联网与的现实生活存在着错综复杂的联系，共同构成了庞大的复杂系统，研究学者将复杂网络当作一种研究客观存在的物理、网络或是现实生活中的一些事件进行建模分析的一种研究手段。对于复杂网络的初步形成最早可以追溯到 1736 年，学者 Euler，他通过研究 解决“七桥 ”问题的办法，提出了一个新的数学分支——图论与集合拓扑，并通 过这一成就被后人称为“ 图论之父 ”。在 20 世纪末期，随着 Erdös 和 Rényi 提出 的随机网络模型、Watts 及 Strogatz 提出的 WS 小世界网络模型（六度分离理论）、Barabási 及 Albert 提出的 BA 无标度网络模型。

随着图论的不断发展，成为了复杂网络研究的基石，为复杂网络拓扑的研究提供了方法。借助图论，复杂网络用N 表示点的集合，用E代表边的集合。根据边是否有方向，可以将网络分为有向网络和无向网络。根据边是否具有权重，可以将网络分为加权网络和无权网络，（一般在《数据结构》这一门课中会学习到）。下图画了一个简陋版，勉强看吧！哈哈哈。

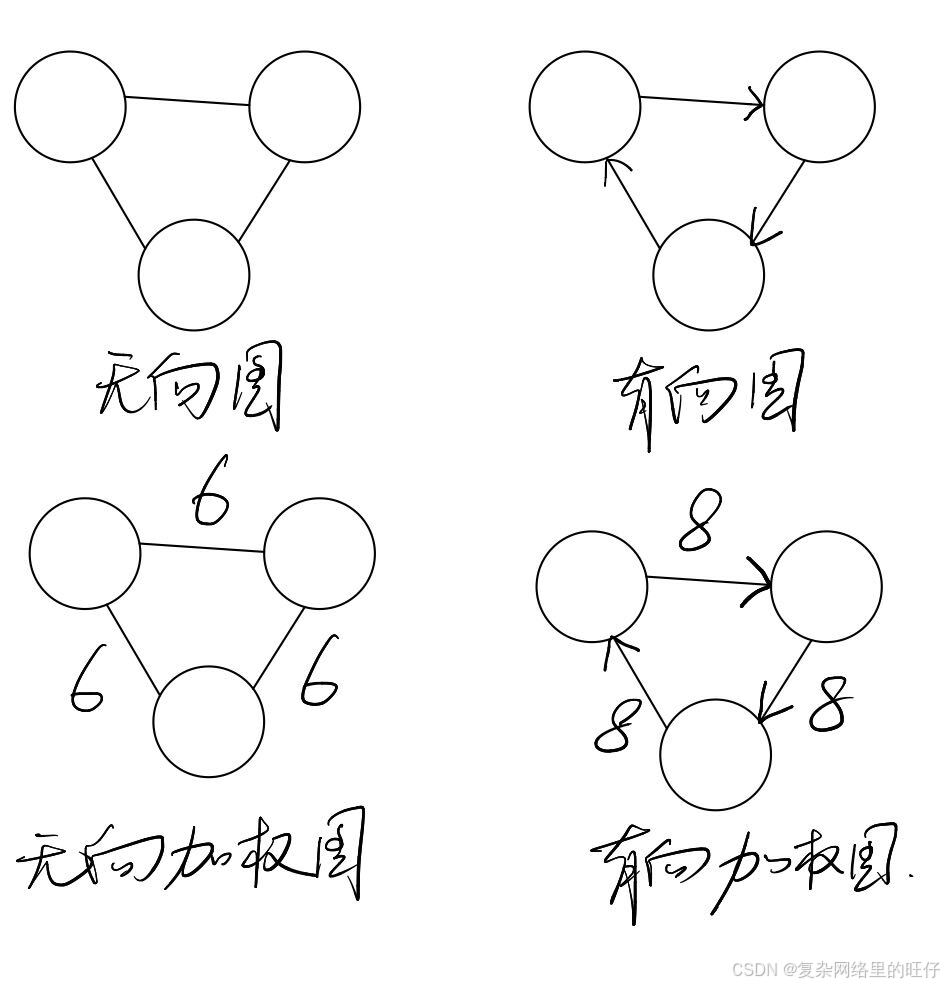
复杂网络的复杂性所在主要体现在结构的复杂性、节点的复杂性、节点间的相互影响、网络间的相互影响等几个方面，因为对于网络来说，整个网络并不是一成不变的，而是随着时间的变化而在实时的变化，而且不同的网络之间也相互影响。

二、复杂网络模型

为更好的研究网络系统拓扑结构对网络系统稳定性的影响，深入探索网络行为和现实网络系统的相互关联，研究者们在研究过程中不仅要结合真实网络，同样也要注重对网络模型的探究。随着复杂网络研究的不断深入，目前非常经典且十分重要的网络模型大致可以分为以下四大类：规则网络、随机网络、小世界网络以及无标度网络。

1.规则网络

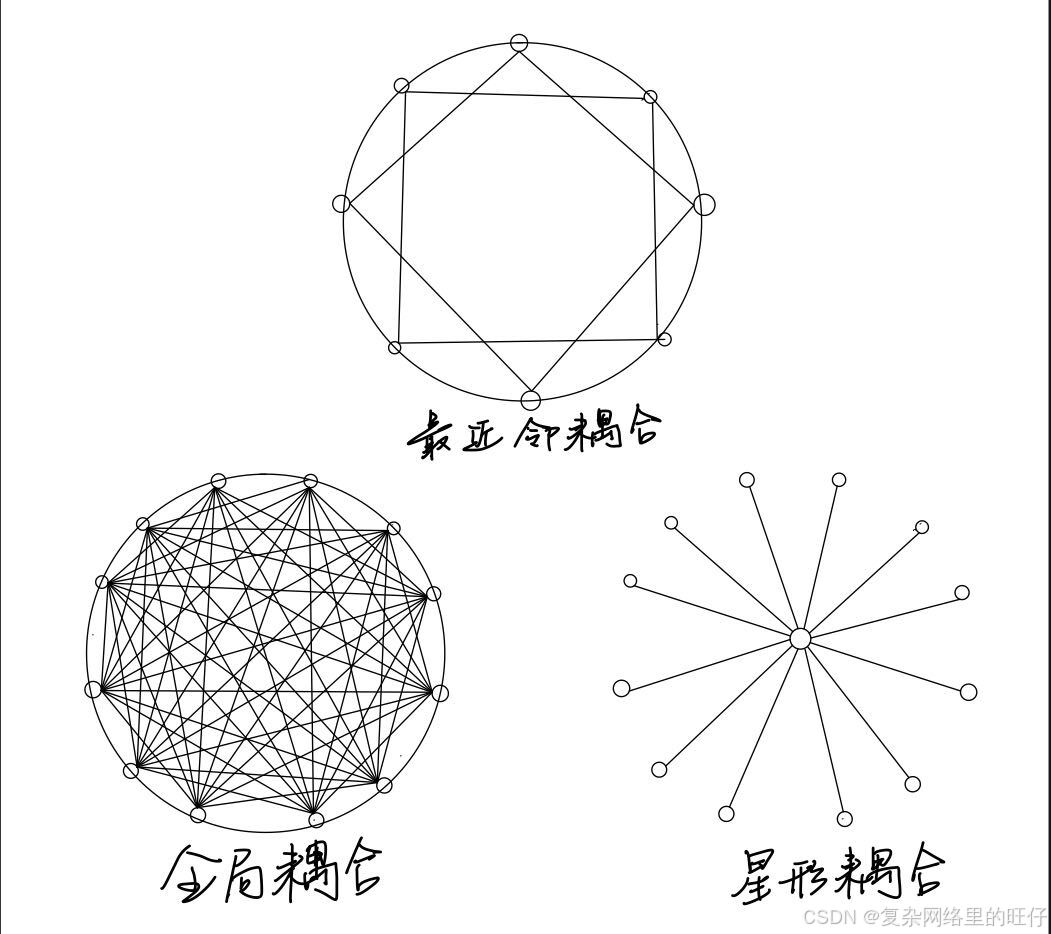
规则网络是所有网络系统模型中最基础的网络模型。同样规则网络也是历史中研究时间最久的网络模型，规则网络具有规则的拓扑结构。比如全局耦合网络(某个节点和网络中其它的节点之间都有连边)、最近邻耦合网络（某个节点除了和邻居节点之间有连边，和邻居的邻居（二阶邻居）之间也有连边）和星形网络（以某个节点为中心节点，其它节点只和中心节点建立连边），示意图如下：

规则网络的度分布为：

生成方法：

G = nx.random_graphs.random_regular_graph(3, 200) 
# 生成了包含200个节点、每个节点有3个邻居的规则图

2.随机网络

随机网络是由Erdös和Rényi提出来的随机网络模型，故也称作ER网络。自从Erdös和Rényi在1957年提出随机图理论之后，随机图理论就变成复杂网络研究当中不可或缺的理论指导。ER模型（随机图模型）是指在给定n个顶点后，规定每两个顶点之间都以p的概率连接起来（0⩽p⩽1），而且这些判定之间两两无关。ER随机网络的度分布遵循泊松分布：

生成方法：

G = nx.random_graphs.erdos_renyi_graph(200, 0.2)
# 生成一个含有200个节点、以概率p = 0.2连接的ER随机图

3.小世界网络

Milgram最早研究发现网络的小世界特性，通过Milgram研究的小世界特性可以发现，在真实网络中，比如社交网络，两个节点之间的最短路径通常比较短。小世界网络是由规则网络中边的随机化重连产生的，所以小世界网络存在于由完全规则网络向完全随机网络的过渡阶段。下图为一个示意图（图片引自文献：Watts D J, Strogatz S H. Collective dynamics of ‘small-world’networks[J]. Nature, 1998, 393(6684): 440-442.）：

生成方法：

G = nx.random_graphs.watts_strogatz_graph(200, 4, 0.3)
# 生成一个含有200个节点、每个节点有4个邻居、以概率p=0.3随机化重连边的WS小世界网络

4.无标度网络

在现实社会的真实网络中，只有一小部分网络节点度很大，大部分网络节点的度值都很小，这样的网络节点度分布满足幂律分布的特性。比如蛋白网络、神经网络、万维网等等。由于此类网络中节点的度没有特别明显的特征长度，所以也被称作无标度网络。典型代表有BA无标度网络、SF网络。SF网络的度分布为：

生成方法（以BA网络为例）：

G = nx.barabasi_albert_graph(300, 3)  
# 创建一个Barabasi-Albert 无标度网络

5.相依网络

在现实生活当中网络并不是单独存在的，网络与网络之间都有一定的依赖关系。每个网络内部也有连接边，网络之间也有连接边。比如电力网络和通讯网络，电力网络为通讯网络提供电力支持，同样通讯网络可以对电力网络提供控制支持，这样两个网络之间相互依赖，促使整个系统的正常运行。

为更好的展示一个双层节点耦合相依网络，以下图中所示的一个模型进行解释说明。在下图中，假设网络A是电力网络，然后网络B是通讯网络，网络内部的连边用实线连接起来，表示网络内部节点之间的联系，这样的边称为连接边，然后网络间的连边用虚线表示，表示网络之间的联系，这种连边称作依赖边。当一个网络中部分节点受到攻击时，网络中其余的节点由于依赖关系可能被间接攻击破坏，比如网络A的一个节点被破坏，会导致网络B中的节点也会被破坏，然后网络B的节点被破坏，又会反馈给网络A，导致网络A的节点又会被破坏，形成级联故障，最终整个网络系统发生崩溃。

但是相依网络分为两种，分别是节点耦合相依网络和边耦合相依网络，对于节点耦合相依网络的研究基本上很成熟了，目前边耦合相依网络的研究受到了研究者们的广泛关注。下图分别给出两种不同耦合方式的示意图：

 三、重要性指标

（1）度和度分布

网络中节点i度d(i) 定义为与节点i 相连的连边总数，若与节点i有连边的连接总数为k，那么节点的度为d(i) =k 。网络中所有节点的度的平均值称为网络的平均度，定义为<k> ，即：

把具有相同度的节点的个数分别统计起来，也就是网络中节点的度分布，用分布函数p(k) 来表示：

 

（2）平均路径长度

网络中任意两个其中N 代表的是网络中节点的总数目，dij 为节点i 与节点j 之间的最短路径。节点之间的最短路径的平均值称为整个网络的平均最短路径。通过表达式L 来表示，：

（3）度相关性

对于某一个网络而言，令D={d1,d2,…,dn} ，其中di 代表的是节点i=1,2,3…,n 的度值。N为网络的节点总数。用(i,j)∈E 来表示节点i 和节点j 之间的连边，那么网络G的度相关系数r(G) 的定义公式为：

（4）最大连通集团

网络一般由多个分支组成，一个分支指的是一个连通的子网络，“最大”代表着原网络中任何其它节点或边遭受到攻击时，形成大小不一的连通子图。把连通子图中阶数最大的一个称为最大连通分支，即最大连通子图，当网络演化成无限网络时，最大连通分支的阶数与整个网络的阶数之比对不同的网络会呈现出不一样的结果，这一比值是衡量网络稳定性的一个重要参数，同时也是网络渗流相变理论中的一个重要参考量。同时，也能从某些方面说明网络的鲁棒性好坏。

整理不易，谢谢各位的点赞，比心！！！