Arduino智能小车（三）：PID算法简介

本篇文章是对PID算法的原理进行了一些探讨，并对其在Arduino智能车中的使用做了简单的介绍。如有纰漏，烦请指出😜

前两篇文章地址：
Arduino智能小车（一）：编码马达
Arduino智能小车（二）：编码马达的使用

PID是控制里面最为经典的一个算法，从智能小车，到扫地机器人，再到工业机械臂，或多或少都在使用这个控制算法。简单而又可靠的特性使其适用于各种场合，而广泛的应用又使之衍生出了各种各样的改进算法。总而言之，PID可谓是控制领域最常用的一个组成部分之一。

PID控制算法简介

PID，这个名字由三个字母组成，P为比例，I为积分，D为微分。而这个算法顾名思义也就是包含三部分：比例(Proportional)，积分(Integral)和微分(Derivative)。

下面我将分别从控制理论和机器人学两个方面分别对PID算法的原理和组成进行探讨。

自动控制原理中的PID

我们从最基础的控制系统开始：

这是一个开环的控制系统，优点是简单，但因为其没有反馈，所以无法保证精度，稳定性也较差，当系统有干扰时，输出有较大的不确定性。为了提高控制的精度和鲁棒性，一般会加入反馈，将反馈以一定的比例和输入量相减得到误差，将误差作为控制量，形成闭环控制系统，当K=1时，即为常见的单位负反馈：

对于我们这里的电机控制而言，反馈量也就是编码器读取到的数据。

而系统的重点就在于控制器(Controller)的设计，根据原理的不同也就产生了各种各样的控制器。

而我们所要介绍的PID则是如下图所示的一个控制器：

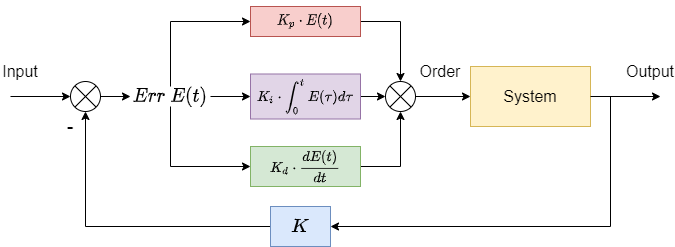
上面所提到的三部分即为分别对误差$E(t)$做比例，积分，微分运算，再加起来作为指令输入给被控制对象。表达式如下：
$$U(t)=K_p\cdot E(t)+K_i{\int }_0^{t}E(\tau )d\tau +K_d\cdot \dot{E}(t)$$

一个例子

我们用一个例子从本质上理解一下这三部分的作用，就以电机控制为例，比如我们要控制电机从0运动到1。

这时，比例环节相当于每隔一段时间加$K_p\cdot Err$，也就是电机速度和误差是成正比的。而当$k_p$越大时，电机将更快的运动到目标位置。

如果只有比例环节的话，当电机受到一个外作用扭矩时，电机最终是不会到1的，而是存在一个稳态误差。因为在到达这一点后，电机输入$K_p\cdot Err$所提供的扭矩已经无法克服外部扭矩作用，于是就停在了这一点。而积分环节的作用就是将误差积分，如果这个误差一直存在的话，积分会越来越大，最终也就表现在电机输入越来越大，也就可以克服这个扭矩继续运动至目标位置，消除稳态误差

开过车的朋友们一定有这个经验，在红绿灯路口前如果速度较快的话，要提前点刹车，使车在线前停下来。微分环节的作用也在于此，其与误差的导数成正比，因为误差是一直在减小的，所以这一项一般是负的，相当于扣除一部分输入。当速度越快，也就是越快的接近目标时，扣除的部分越多，这一作用使得电机提前减速，起一个缓冲的作用，也避免了超调和振荡的出现。

传递函数表示

在经典控制理论中，习惯采用传递函数来描述控制系统，传递函数是指输出和输入的拉普拉斯变换之比。对上式求拉普拉斯变换，可得：
$$\begin{gathered} U(s)=K_{p}E(s)+K_i\frac{1}{s}E(s)+K_{d}sE(s) \\ =K_p(1+\frac{1}{T_{i}s}+T_{d}s)E(s) \end{gathered}$$
式中涉及到的参数关系为$K_i=\frac{K_p}{T_i}$，$K_d=K_p{T}_d$，而PID控制器性能的关键影响因素即为$K_p,K_i,K_d$这三个参数，这三个参数的整定也是设计PID控制器的重点部分。整定参数的方法暂时不表，我们下篇文章再做深入介绍。下面我们从另外一个角度去了解PID。

机器人学中的PID

这学期学习了机器人学，我们用了John J.Craig的**《机器人学导论》**作为教材，这本书中的最后几章对PID的介绍是从一个对我来说很“新鲜”的角度切入的，还挺有意思的。为了能彻底搞懂，我在这里做一些探讨。

首先考虑一个“单关节”机械臂，简单起见，该关节为移动关节：

这里我们假定关节处在一个势场中，其势能函数为$V(x)=\frac{1}{2}{k}_p(x-x_d{)}^2$，$x_d$为目标位置，也就是关节处在目标位置时势能最低，而我们控制的目标也就是让关节的势能最低。这里利用了势能总是趋向于更低的地方这一原理设计了我们的控制算法。我们用弹性势能来类比我们所假定的势能，这样一来，就可以把左面的关节看作右面的系统。

机器人PD控制

先不考虑摩擦力及其他外力，由简单的受力分析很容易得到关节力表达式：
$$f=m\ddot{x}=-\frac{\partial V(x)}{\partial x}=-k_p(x-x_d)$$
上式即表达了一个简单的比例控制，接下来我们加入摩擦力：
$$f=-k_p(x-x_d)-k_v\dot{x}$$
接下来是一个神奇的处理，要看仔细了。我们把控制器分为两部分，一部分基于模型(Model-Based)，一部分基于伺服控制(Servo-Based)。基于模型的部分基于的就是机器人的模型；而伺服控制的部分比较贴近我们这里探讨的PID。

之前我们已经知道$f=m\ddot{x}$，但实际上机器人正常工作时，因为各种因素影响还会引入一个非线性环节$b(x,\dot{x})$，因此：
$$f=m\ddot{x}+b(x,\dot{x})$$
这就是基于模型的部分，这一部分不做详细介绍，看不懂没关系。我们只关心伺服控制部分，所以接下来将Model-Based这部分剔出来：
$$f=m\ddot{x}+b(x,\dot{x})=\alpha f^{\prime }+\beta$$
形成类似下图的控制部分：

而显而易见的是，此时$f^{\prime }=\ddot{x}$，再代入上面受力分析的式子中可得：
$$\begin{gathered} m{f}^{\prime }=m\ddot{x}=-k_p(x-x_d)-k_v\dot{x}=m[-k_p^{\prime }(x-x_d)-k_v^{\prime }\dot{x}] \\ \Rightarrow f^{\prime }=-k_p^{\prime }(x-x_d)-k_v^{\prime }\dot{x} \end{gathered}$$
此时我们就得到了一个比例-微分(PD)控制的式子。观众朋友们或许也注意到了，这里的控制都是给定一个目标位置，控制关节运动到目标位置并停在这里（速度为0）。而对机器人做轨迹规划后得到的是轨迹上的目标位置，以及此时的目标速度和目标加速度。因此我们可以将关节力取为：
$$f^{\prime }={\ddot{x}}_d-k_v^{\prime }(\dot{x}-{\dot{x}}_d)-k_p^{\prime }(x-x_d)$$
由于$f^{\prime }=\ddot{x}$，移项可得：
$$\begin{gathered} (\ddot{x}-{\ddot{x}}_d)+k_v^{\prime }(\dot{x}-{\dot{x}}_d)+k_p^{\prime }(x-x_d)=0 \\ \Rightarrow \ddot{e}+k_v^{\prime }\dot{e}+k_p^{\prime }e=0 \end{gathered}$$
也就是说我们最后的控制目的是要让位置，速度和加速度误差均为0。

机器人PID控制

但是这样的控制仍然存在一定的问题：比如关节受一个干扰力$f_{dist}$时，系统到达稳态后会有一个稳态误差：
$$\Delta x=\frac{f_{dist}}{k_p}$$
这个稳态误差可以用积分来表示：
$$k_p\Delta x=k_i\int (x-x_d)dt$$
此时系统受力分析就变成了：
$$f+f_{dist}=m\ddot{x}+b(x,\dot{x})$$
将基于模型的控制规律代入可计算出$f^{\prime }=\ddot{x}-\frac{f_{dist}}{m}$

于是我们在上面的$f^{\prime }$再加上这一个积分项得到如下比例-积分-微分(PID)控制规律：
$$\begin{gathered} f^{\prime }={\ddot{x}}_d-k_v^{\prime }(\dot{x}-{\dot{x}}_d)-k_p^{\prime }(x-x_d)-\frac{f_{dist}}{m} \\ ={\ddot{x}}_d-k_v^{\prime }(\dot{x}-{\dot{x}}_d)-k_p^{\prime }(x-x_d)-k_i^{\prime }\int (x-x_d)dt \end{gathered}$$
稍作移项我们就能发现这一控制规律的本质：
$$\begin{gathered} \ddot{e}+k_v^{\prime }\dot{e}+k_p^{\prime }e+k_i^{\prime }\int edt=\frac{f_{dist}}{m} \\ \stackrel{两边求导}{\to }\dot{}\ddot{e}+k_v^{\prime }\ddot{e}+k_p^{\prime }\dot{e}+k_i^{\prime }e=0 \end{gathered}$$
也就是说，我们PID控制的最终目的是使位置的误差，速度的误差，加速度的误差，甚至加加速度的误差都等于0。对于机器人的运动来说，当然是能越多的控制其运动过程中的参数，越能使其平稳的运动，也就越能达到良好的效果。

最终我们的控制框图如下：

Arduino上的PID算法

原理讲了很多，或许读者已经晕晕乎乎，似懂非懂了，不过没有关系，我们不求甚解，直接从Arduino上实现PID控制入手，做一些实用的介绍。

离散化

在使用我们上面得到的式子前，还需要进行一步工作：离散化。毕竟我们不可能时时刻刻采样计算，输出连续的指令，这对于我们的控制系统来说是不现实的。正常的操作是以一定周期进行采样，计算，然后每隔一段时间给一个指令，输出的一个离散化的信号。

我们假设系统的采样周期为T，以第K次采样为例。此时积分就可以表示为：${\sum }_{i=1}^{k}E(i)$，而微分则为：$E(k)-E(k-1)$，那上面的式子离散化后就为：
$$U(k)=K_{p}E(k)+K_i\sum _{i=1}^{k}E(i)+K_d\left[E(k)-E(k-1)\right]$$

位置式PID

直接采用上面的离散化公式，很容易写出代码：

int PositionPID(int target_high, int target_low)
{
    //bias为E(k)，intergral_bias为积分项，last_bias为E(k-1)，m为电机编码器读取到位置数据(反馈量)
  	static float bias, result, intergral_bias, last_bias;
  	if (m > target_high)
    	bias = target_high - m;
  	else if (m < target_low)
    	bias = target_low - m;
  	else
  	{
    	bias = 0;
    	intergral_bias = 0;
  	}
  	intergral_bias += bias;
  	result = Position_KP * bias + Position_KI * intergral_bias + Position_KD * (bias - last_bias);
  	last_bias = bias;
  	return result;
}

注意到上面的函数有两个target输入，这里是设定了一个目标阈，只要达到了target_low到target_high之间，就算达到了目标位置。这样操作增加了一定的稳定性，在一定程度上减小了振荡的可能性。

另外要注意bias，intergral_bias，last_bias变量类型是static float，这样会使其值保存到下一次计算，而不是随着该函数返回而清空。

增量式PID

除了位置式PID外，还有一种改进算法叫做增量式PID。所谓增量式，指的是我们每次不是计算$U(k)$，而是$\Delta U$。其计算公式为：
$$\begin{gathered} \Delta U=U(k)-U(k-1) \\ =K_p\left[E(k)-E(k-1)\right]+K_{i}E(k)+K_d\left[E(k)-2E(k-1)+E(k-2)\right] \end{gathered}$$
根据这个式子写出函数：

float VelocityPID(float target)
{
  	static float bias, result, last_bias, last_dif_bias;
  	bias = target - velocity;
    dif_bias = bias - last_bias;
  	result += Velocity_KP * dif_bias + Velocity_KI * bias + Velocity_KD * (dif_bias - last_dif_bias);	//注意这里是result+=
  	last_dif_bias = dif_bias;
  	last_bias = bias;
  	return result;
}

值得一提的是，增量式PID一般用于速度控制，也就是给定目标速度，得到电机输入。且一般只用PI两个参数，D为0。

另外，增量式没有$\sum$运算，增量只由最近几次的采样值有关，因此偏差带来的影响较小，累计误差也小。

PID库

Arduino上有PID库，这个库贼好用👍，推荐大家用一用。可以使用Library Manager进行安装。具体的介绍在这里，例子很清楚，这里就不做详细介绍了。大神还对这个库的原理进行详细介绍，感兴趣的可以移步原文👈观看研究，(这里有翻译)