有一个8*8的方格棋盘（如下图所示），现有一匹马从任意一个位置（方格）出发，给出一种方案使马走遍棋盘中的每一个方格，且每个方格只走过一次（马走日字）。

马踏飞燕基本思路

被初始化的全局变量：棋盘、可能马可以走到的点的坐标

自定义函数：nextpos、movenext

主函数功能：

1. 输入马现在初始的坐标位置
2. 根据坐标位置去寻找马的出口点
   1. 出口点：在棋盘上，将所有坐标的值设置为0，如果此刻马走过这个点，那么在这个坐标位置下将其值设置为这是第几步走过的这个坐标
   2. 出口点的寻找方式：nextpos方式
      1. 在自定义的nextpos方法中，我们采取了这种方式来寻找出口点：我们将马当前位置的坐标进行输入，然后利用for循环：
         1. 对所有可能走到的点进行边界的判断，如果下一步马走出了棋盘，那么直接结束这步循环，进入到下一步的循环中。
         2. 如果在棋盘中，那么需要对这点的值进行判断，只有这点的值不为0，那么才是没走过的点，否则就是已经走过的点。如果是已经走过的点，那么跳过当前的这步循环。
         3. 如果没有走过，那么就进行count（共有几个出口值点）进行更新（累加），同时更新可以作为出口的点的坐标（利用二维数组）。
      2. 最后对这点的count进行输出
3. 寻找完当前坐标的所有出口点之后，就需要选择一个出口点进行选择，选择采取的策略是剪枝。方式：movenext
   1. 剪枝的概念是：逐步的去选择可能性最小的坐标点，然后对其进行选择。不断的缩小可能性。
   2. 具体的实施步骤是：
      1. 首先将当前点的坐标点进行带入。
      2. 然后根据我们在nextpos中更新的可能作为pos点的坐标，进行预测：
         1. 预测的概念是：拿着下一步可能走到的点，然后根据这点进行出口点的计算，将预测的结果进行返回。
         2. 具体的实现是依靠for循环，不断的去更新最小出口点数（设置了一个条件：下一步的出口点数不应该大于8，因为最大只有8个出口点（8种走出的路线）），同时更新当前最小点的坐标。直到遍历结束所有的出口点，结束循环。
         3. 通过全局变量记录当前点为找到的下一步中拥有最小出口点的点的x，y方向移动量。同时返回这个点的出口点数。
4. 通过for循环，同时通过我们设置的全局变量（下一步分别在x，y方向的移动量被我们通过movenext记录），来不断的对下一步点的坐标进行更新。for循环中设置的条件step为累加量，step<64:因为设置的棋盘的大小是8*8大小的，所以最多有64步，我们将step赋给每个下一步，得出了整个棋盘的每个点的被马经过的顺序。
5. 将棋盘每个点的值输出，为我们找到的路径。
6. 程序结束。

#include <cstdio>
#include <cstdlib>
int move1[8]={2,2,1,1,-1,-1,-2,-2,},
        move2[8]={1,-1,2,-2,2,-2,1,-1,},
        board[8][8]={{0}};
int nexti[8],nextj[8],npos,cur_row,cur_col,step,outwrite=1;

/*函数nextpos计算位置（i，j）出口个数*/
int nextpos(int i,int j,int a[8],int b[8])
{
    int count=0,k,i1,j1;
    for(k=0;k<8;k++){
        i1=i+move1[k];
        j1=j+move2[k];
        if(i1>7||i1<0||j1>7||j1<0)
            continue;
        else if(board[i1][j1]!=0)
            continue;
        else{
            a[count]=move1[k];
            b[count]=move2[k];
            ++count;
            printf("i is %d\n",a[count]);
            printf("j is %d\n",b[count]);
        }
    }

    return(count);
}

/*函数movenext在有多出口时，选择适当出口推进一步*/
int movenext(int *i,int *j,int a[],int b[])
{
    int temp,count=8,a1[8],b1[8],
            nexti_like[8],nextj_like[8],
            cur_row_like,cur_col_like,k,t;

    for(k=0;k<npos;k++)
    {
        temp=nextpos(*i+nexti[k],*j+nextj[k],a1,b1);
        if(temp<count)
        {
            cur_row_like=*i+nexti[k];
            cur_col_like=*j+nextj[k];
            count=temp;
            for(t=0;t<count;t++)
            {
                nexti_like[t]=a1[t];
                nextj_like[t]=b1[t];
            }
        }
    }
    *i=cur_row_like;
    *j=cur_col_like;
    for(k=0;k<count;k++)
    {
        a[k]=nexti_like[k];
        b[k]=nextj_like[k];
    }
    return count;
}


int main()
{
    int i,j;
    printf("\nEnter the starting position(row,col):");
    scanf("%d",&cur_row);/*输入起始位置*/
    scanf("%d",&cur_col);
    board[cur_row][cur_col]=1;
    npos=nextpos(cur_row,cur_col,nexti,nextj);
    printf("nexti is %d",nexti[0]);
    printf("出口数量为 %d",npos);
    for(step=2;step<=64;step++)
    {
        if(npos==0){
            outwrite=0;
            break;
        }
        else if(npos==1){
            cur_row+=nexti[0];
            cur_col+=nextj[0];
            board[cur_row][cur_col]=step;
            npos=nextpos(cur_row,cur_col,nexti,nextj);
        }
        else{
            npos=movenext(&cur_row,&cur_col,nexti,nextj);
            board[cur_row][cur_col]=step;
        }
    }
    if(outwrite==0)
        printf("\n no solution\n");
    else{
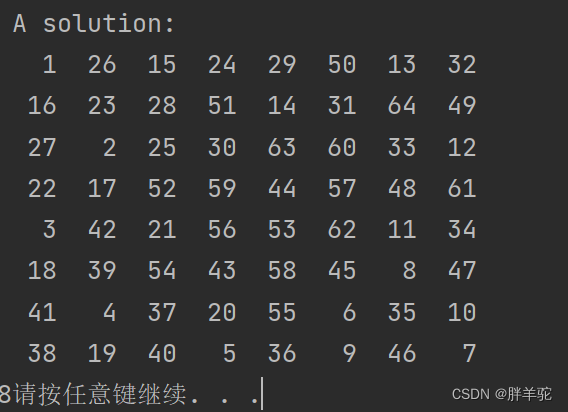
        printf("\n A solution:\n");
        for(i=0;i<8;i++){
            for(j=0;j<8;j++)
                printf("%4d",board[i][j]);
            printf("\n");
        }
    }
    printf("%d",board[5][6]);
    system("pause");
}

输出的是为马走过的点的顺序。