论文阅读笔记(4):带剪枝的局部凸表达进行流形聚类
注:Local Convex Representation with Pruning for Manifold Clustering
本文很短,快速带过。
介绍
真实世界中高维数据可以用多个低维流形的并表示,流形聚类的目标就是把数据X的列(也就是batch中每一个数据点)指派到对应的子流形结构中。
流形结构一般不会剧烈变化,因此我们可以假设流形是局部平坦的。对这些平坦的局部上的数据点进行聚类就变成了线性(或仿射)的子空间聚类。子空间聚类的方法主要有两步:
- 学习数据点之间的两两关系,即affinity矩阵
- 对affinity矩阵应用谱聚类
其中,影响聚类效果最重要的自然是如何构建affinity矩阵。目前SOTA方法是基于自表达模型的方法,也就是把每个数据点用其它数据点线性表出,权重用于计算affinity矩阵的元素,偏置即为容忍误差。之后affinity的元素为 a i j = 1 / 2 ∣ c i j + c j i ∣ a_{ij}=1/2|c_{ij}+c_{ji}| aij=1/2∣cij+cji∣,即对数据点 i → j i\rightarrow j i→j与 j → i j\rightarrow i j→i的关系做一个平滑。此外,子空间保持性质要求:被表出的数据点和非零系数 c j c_j cj对应的数据点来自同一个子空间,而零系数对应数据点位于其它子空间。
但是!若把线性性质从local直接扩展到global显然是不适合流形结构的。
当流形结构是高度非线性的时候,子空间聚类不再有效。现有的聚类非线性流形方法可分为global方法和local方法。
全局方法 假设流形具有不同的内在维数(intrinsic dimensions),数据可以根据维数而不是流形本身进行聚类。然而在许多实际问题中,不同的流形可能仍然具有相同的内在维数。
局部方法 通常构造一个pairwise的affinity来描述局部几何结构,然后谱聚类。例如,在拉普拉斯特征映射(Laplacian Eigenmap)中使用局部邻近(local proximity);或使用局部线性(local linearity);或使用曲率(curvature )信息;或研究主角度(principal angle)信息;或探索稀疏表示(sparse representation)方法。
*注:Pairwise 不关注精确的预测每个数据之间的的精确affinity关系,而主要关心两两数据之间的顺序
其中,基于局部自表达模型的方法因其简洁有效而备受关注,如之前提到的基于局部线性的方法和基于加权稀疏表示的方法。然而,它们要么需要复杂的调参,要么缺乏理论依据。
文章主要贡献
大概两个
理论上:局部凸表达(Local Convex Representation, LCR)
找到数据点 x j x_j xj的k-最近邻个点的仿射稀疏表示其实就是解决以下问题:
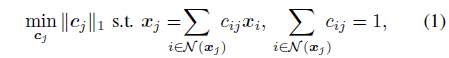
*注:约束条件保证线性表达,1范数保证稀疏,不属于 N ( x j ) \mathcal N(x_j) N(xj)的数据点系数为0。
如果 x j x_j xj位于数据点集 { x i , i ∈ N ( x j ) } \{x_i,i\in \mathcal N(x_j)\} {xi,i∈N(xj)}的凸包络的相对内部,那么最优解的系数一定是非负的。根据这一假设,上式变为:
*注:这也是为什么方法被叫做局部凸表达
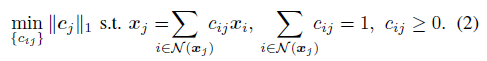
对于k近邻的点,属于同一子流形
M
(
ℓ
)
\mathcal M^{(\ell)}
M(ℓ)的点作为组成矩阵
X
j
(
ℓ
)
X_j^{(\ell)}
Xj(ℓ),而属于其它子空间的点作为
X
j
(
−
ℓ
)
X_j^{(-\ell)}
Xj(−ℓ)。若点
x
j
x_j
xj属于
X
j
(
ℓ
)
X_j^{(\ell)}
Xj(ℓ)的凸包络的相对内部,并且
X
j
(
ℓ
)
X_j^{(\ell)}
Xj(ℓ)的仿射包络与
X
j
(
−
ℓ
)
X_j^{(-\ell)}
Xj(−ℓ)的凸包络不相交,那么可以保证最优解的非零系数对应的数据点都来自同一子流形。
我们把等式约束进行最小二乘relax,如下:
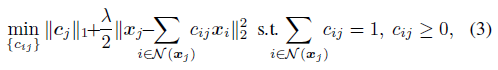
根据系数非负性约束的假设,公式(3)的等价优化可以省去调参
λ
\lambda
λ,如下:
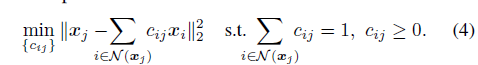
*注:由于 c i j ≥ 0 c_{ij}\geq0 cij≥0,1范数( ∑ ∣ c i j ∣ \sum|c_{ij}| ∑∣cij∣)的绝对值是可省略的,又元素的累和已经被等式约束为1了,故 ∣ ∣ c j ∣ ∣ 1 ||c_j||_1 ∣∣cj∣∣1可省略,于是参数 λ \lambda λ也省略了。
当问题(4)是convex-LLE的子问题时,我们从上面的推导中看到,对于那些相对的内点,公式(4)是一个具有非负仿射约束的 ℓ 1 \ell_1 ℓ1最小化问题。类似地,我们还可以证明,相对内点的问题(4)最优解中的非零系数能够在温和的条件下检测出哪些点属于同一子流形。
*疑问:如果LCR的公式(4)可以被作为convex-LLE的子问题,那么它是否有不同于其它方法的创新?
剪枝方法:估计流形的内在维数以剪除次要非零系数
由于问题(4)没有对小系数进行阈值,我们采用流形内在维数作为线索对这些小系数进行剪枝。虽然可以通过不同的方法,但这里使用最经典的方法——局部PCA,它检查局部协方差矩阵的特征值谱,即在每个数据点的邻域执行局部PCA。具体来说,该过程的第一步是计算每个数据点的局部PCA。然后,我们取整个数据集上特征值的平均值,并通过保留95%能量时得到的特征值的个数来估计本征维数。
一旦内在维数 d ^ \hat d d^被估计,保留 d ^ + 1 \hat d+1 d^+1个最大的非负系数,并将其余小系数设置为零。这样只保留 ( d ^ + 1 ) (\hat d+1) (d^+1)-近邻的连接,它们很可能来自同一个子流形。
实验
人工数据
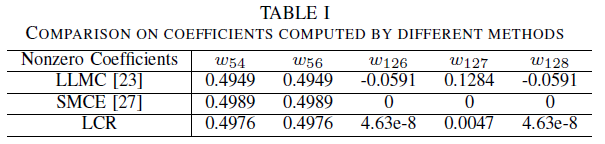
先在两个互相靠近的圆环上验证,发现靠近的点附近容易误判,那么SMCE将不同子流形的点系数全部化为0,而LCR非常接近零(1e-3的级别),LLMC则出现误判(点127的权重),在不剪枝的情况下性能:LLMC<LCR<SMCE
在三叶结的较复杂人工数据上性能:LCR<LLMC<SMCE,但是剪枝方法提高了LCR和LLMC的性能,LCR+
d
^
\hat d
d^的性能已经可以和调参
λ
\lambda
λ后的SMCE相媲美。

实际数据
LCR+
d
^
\hat d
d^在COIL-20,COIL-100和UMIST上都取得最佳效果

但是需要注意,之前在人工数据上剪枝方法能够提高LLMC的性能,在真实数据集上去反而降低了LLMC的性能。
这是为什么?文章没有给出分析
文章还给出了k-近邻的个数对方法性能的影响,随着k增大多数方法新能下降,而LCR+剪枝的方法准确率却飙到很高,如下图所示。
按道理k个数越多流形越难保持在局部平坦的区域上,可能是因为剪枝的方法把 d ^ + 1 \hat d+1 d^+1到 k k k的系数给裁剪掉了。但是就算如此,相比其它方法甚至可以说准确率好到不可思议,不过这是为什么呢?文章没有给出具体的解释。






















 6111
6111











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








