论文阅读笔记(5):Oracle Based Active Set Algorithm for Scalable Elastic Net Subspace Clustering,基于Oracle的可伸缩弹性网络子空间聚类有效集算法
注:16年CVPR,老文章,但是个人觉得写得很好而且系统
摘要
子空间聚类的SOTA方法基于自表达模型,同 ℓ 1 \ell_1 ℓ1、 ℓ 2 \ell_2 ℓ2或核范数正则化系数矩阵。 ℓ 1 \ell_1 ℓ1正则化保证在广泛的理论条件下给出一个保持子空间的完整性(即,不同子空间的点之间没有连接),但同一子空间内的点可能同样没有连接。 ℓ 2 \ell_2 ℓ2和核范数正则化通常会改善连通性,但只有在子空间独立时能够保证给出子空间保持的affinity。混合 ℓ 1 \ell_1 ℓ1、 ℓ 2 \ell_2 ℓ2和核范数的正则化在子空间保持和连通性之间提供了一种平衡,但这是以增加计算复杂度为代价的。本文研究了弹性网正则化器( ℓ 1 \ell_1 ℓ1、 ℓ 2 \ell_2 ℓ2范数的混合)的几何结构,并利用它导出了一种可证明正确的、可扩展的确定最优系数的有效集方法。我们的几何分析也为弹性网络子空间聚类的连通性( ℓ 2 \ell_2 ℓ2正则化)和子空间保持( ℓ 1 \ell_1 ℓ1正则化)之间的平衡提供了理论上的证明和几何解释。我们的实验表明,所提出的有效集方法不仅具有最先进的聚类性能,而且能够有效地处理大规模数据集。
1. 介绍
子空间聚类得到广泛关注,其中谱聚类最为受欢迎。这些方法的步骤分为两步(参见论文阅读笔记4),即学习affinity然后谱聚类。其中第一步最为重要,即最为合理的affinity矩阵。优化目标如下
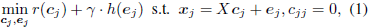
其中
c
j
c_j
cj是affinity系数,
e
j
e_j
ej是噪声或误差,
r
(
⋅
)
r(\cdot)
r(⋅)和
h
(
⋅
)
h(\cdot)
h(⋅)分别是应用的正则化项,
γ
\gamma
γ是平衡系数。所有SOTA方法之间的区别也主要就在正则化项的选择上。
SSC使用的是
ℓ
1
\ell_1
ℓ1范数于是导致了连通性问题,进而产生错误的过分割。其它近年提出的方法如正交匹配追踪(OMP)和最近邻子空间(NSN)也遇到了同样的问题。
作为一种替代方式,最小二乘回归(LSR)使用的
ℓ
2
\ell_2
ℓ2范数使得自表达矩阵更加稠密,缓解了
ℓ
1
\ell_1
ℓ1范数带来的连通性问题。但是它只能在子空间独立时得到的子空间保持解。基于核范数的如低阶表达(LRR)和低阶子空间聚类(LRSC)遇到了同样的问题。
*注:子空间独立意味着子空间的并的维度等于子空间的维度的累和: d i m ( ⋃ S k ) = ∑ d i m ( S k ) dim(\bigcup S_k)=\sum dim(S_k) dim(⋃Sk)=∑dim(Sk)
LRSSC使用了
ℓ
1
\ell_1
ℓ1和核范数的混合,然而,LRSSC给出的改善连通性的理由仅仅是实验性的。一种混合
ℓ
1
\ell_1
ℓ1、
ℓ
2
\ell_2
ℓ2范数的方法如下:
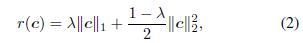
然而该方法的益处没有理论上的证明。其他子空间聚类正则化器分别使用trace lasso和k-support核范数。然而同样没有进行理论上的论证。
上述方法的另一个问题是,它们没有提供有效的算法来处理大规模数据集。为了解决这个问题,[5]建议通过从X中采样的几个锚定点来确定X的表示,然后在锚图上执行谱聚类。在[33]中,作者建议对原始数据的一小部分进行聚类,然后根据所学的组对其余的数据进行分类。然而,这两种策略都是次优的,因为它们牺牲了计算效率的聚类精度。
主要贡献
在本文中,我们使用 ℓ 1 \ell_1 ℓ1和 ℓ 2 \ell_2 ℓ2范数来平衡子空间的保持性和连通性。具体来说,该方法使用SSC和LSR的组合,当λ=1和λ=0时,分别退化成SSC和LSR。在统计学文献中,使用这种正则化的优化称为弹性网(Elastic Net),用于回归问题中的变量选择。因此,我们将这种方法称为EnSC。
- 我们提出了一个有效且可证明正确的基于有效集的算法来解决弹性网络问题。该算法利用了弹性网解的非零项落入oracle region的事实,我们使用oracle区域来定义和高校地更新有效集。提出的更新规则引导了一个迭代算法,该算法在有限的迭代次数内收敛到最优解。
- 我们提供了EnSC生成的子空间保持解条件的理论,以及子空间保持性和连通性之间平衡的清晰几何解释。我们的条件依赖于数据分布的局部界定,这比先前的全局界定有所改进。
- 通过实验证明了该方法在聚类精度和可扩展性方面的优越性。
2. 弹性网:几何解释与新算法
在这一部分中,我们研究了弹性网络优化问题,并提出了一种新的基于有效集的优化算法来解决它。考虑目标函数:
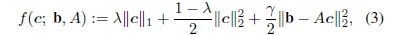
在不失一般性地(Without loss of generality),我们假设
b
\textbf b
b和
A
=
{
a
j
}
j
N
A=\{a_j\}_j^N
A={aj}jN在我们的分析中被归一化为单位
ℓ
2
\ell_2
ℓ2范数。然后弹性网模型计算:
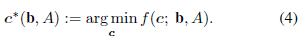
因为由
ℓ
1
\ell_1
ℓ1和
ℓ
2
\ell_2
ℓ2范数组成的
f
(
c
;
b
,
A
)
f(c;{\bf b},A)
f(c;b,A)是强凸的,故得到的
c
∗
(
b
,
A
)
c^*({\bf b},A)
c∗(b,A)(以下简写为
c
∗
c^*
c∗)是唯一的。为了求解公式(4),我们对其进行了几何分析,并利用此分析设计了一个弹性网有效集算法。
2.1 弹性网的几何结构
我们首先给出oracle点的含义
定义2.1
对于公式(4),oracle point被定义为:
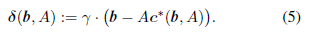
当没有混淆的风险时,我们省略了oracle点对
b
{\bf b}
b和
A
A
A的依赖性——将
δ
(
b
,
A
)
δ({\bf b},A)
δ(b,A)缩写为
δ
δ
δ。注意,oracle点是唯一的,因为
c
∗
c^∗
c∗ 是唯一的,并且在得到最优解
c
∗
c^∗
c∗ 之前无法计算对应的oracle点。下一个结果给出了涉及oracle点的关键关系,该关系由我们的active set方法推导。
定理2.1
公式(4)中
c
∗
c^∗
c∗ 的解满足以下等式:
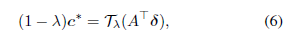
其中,
τ
λ
(
⋅
)
\tau_\lambda(\cdot)
τλ(⋅)是施加在
A
T
δ
(
b
,
A
)
A^T\delta({\bf b},A)
ATδ(b,A)上的软阈值算子,即
τ
λ
(
v
)
=
s
g
n
(
v
)
(
∣
v
∣
−
λ
)
,
\tau_\lambda(v)=sgn(v)(|v|-\lambda),
τλ(v)=sgn(v)(∣v∣−λ), if
∣
v
∣
>
λ
|v|>\lambda
∣v∣>λ
个人对oracle point的理解:
定理2.1表明,如果已知oracle点 δ δ δ,则对应的解 c ∗ c^∗ c∗ 可以直接写出来。可知当且仅当 b = 0 {\bf b}=0 b=0时 δ = 0 δ=0 δ=0。
*注:由公式(3)(4)知当 b = 0 {\bf b}=0 b=0时二范数的最优点在 c ∗ = 0 c^*=0 c∗=0处,由(5)知 δ = 0 δ=0 δ=0
在图1中,我们描述了弹性网问题在不同折衷参数λ值下的二维解。数据矩阵 A A A包含二维欧氏空间中随机分布的100个点,也就是图中的x轴和y轴。z轴则表示了每个系数 c ∗ c^* c∗的量级,红色点则为oracle点,其方向为红色虚线,即和中心点之间的直线段, γ γ γ的值固定为50, λ λ λ的值如图所示变化。

正如所料,随着
λ
λ
λ的减小,
ℓ
2
\ell_2
ℓ2比重增大,解
c
∗
=
0
c^*=0
c∗=0变得更加稠密。此外,如定理2.1所预测的,系数
c
∗
c^*
c∗的大小是对应的字典原子
a
j
a_j
aj和oracle 点
δ
δ
δ(以红色显示)之间角度的衰减函数。
如果
a
j
a_j
aj离oracle点
δ
δ
δ足够远以至于满足
∣
<
a
j
,
δ
>
∣
≤
λ
|\left< a_j, δ\right>|\leq \lambda
∣⟨aj,δ⟩∣≤λ时,根据软阈值函数。对应的
c
∗
c^*
c∗为0。因此我们把包含非零
c
∗
c^*
c∗的
δ
\delta
δ区域称为oracle区域。我们可以用度量两个向量一致性的
μ
(
⋅
,
⋅
)
\mu (\cdot , \cdot)
μ(⋅,⋅)来定义oracle区域:
μ
(
v
,
δ
)
:
=
∣
<
v
,
δ
>
∣
∣
∣
v
∣
∣
2
⋅
∣
∣
δ
∣
∣
2
\mu(v,\delta):=\frac{|\left< v, δ\right>|}{||v||_2\cdot ||\delta||_2}
μ(v,δ):=∣∣v∣∣2⋅∣∣δ∣∣2∣⟨v,δ⟩∣
定义2.2 Oracle Region
对于公式(4),orcale region被定义为:
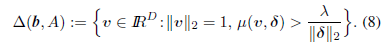
orcale region由一对正反对称的球形盖构成,由
∣
∣
v
∣
∣
2
=
1
||v||_2=1
∣∣v∣∣2=1的约束知它在
R
D
\mathbb R^D
RD的单位球面上,结合
∣
∣
v
∣
∣
2
=
1
||v||_2=1
∣∣v∣∣2=1和
μ
(
v
,
δ
)
\mu(v,\delta)
μ(v,δ)定义可知,对称中心为
δ
∣
∣
δ
∣
∣
2
\frac{\delta}{||\delta||_2}
∣∣δ∣∣2δ,角度半径为
θ
=
a
r
c
c
o
s
(
λ
/
∣
∣
δ
∣
∣
2
)
\theta = arccos(\lambda / ||\delta||_2)
θ=arccos(λ/∣∣δ∣∣2)。如图2所示。当且仅当
a
j
∈
Δ
(
b
,
A
)
a_j\in \Delta({\bf b},A)
aj∈Δ(b,A)时有
c
∗
≠
0
c^*\neq 0
c∗=0,换句话说就是
c
∗
c^*
c∗的支撑集就是落在oracle region中的那些数据点
a
j
a_j
aj。

oracle region捕获到了 矩阵
A
A
A删除列或新添列时 解的变化。这为解决优化问题的有效集方法的设计提供了关键的见insight。
命题2.1
对于任何
b
∈
R
D
,
A
∈
R
D
×
N
{\bf b}\in \mathbb R^D,A\in \mathbb R^{D\times N}
b∈RD,A∈RD×N并且
A
′
∈
R
D
×
N
′
A'\in \mathbb R^{D\times N'}
A′∈RD×N′。如果oracle region
Δ
(
b
,
A
)
\Delta ({\bf b},A)
Δ(b,A)不包含
A
′
A'
A′中的任何列,那么有:
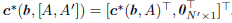
对以上命题的理解是:在向字典
A
A
A添加新的列时,只要新的列不在oracle region
Δ
(
b
,
A
)
\Delta ({\bf b},A)
Δ(b,A)中,那么
c
∗
(
b
,
A
)
c^*({\bf b},A)
c∗(b,A)的解是不会改变的(相当于添加了模值为0的填充)。同样,不在oracle region
Δ
(
b
,
[
A
,
A
′
]
)
\Delta ({\bf b},[A,A'])
Δ(b,[A,A′])中的列被删除时也不会改变
c
∗
(
b
,
A
)
c^*({\bf b},A)
c∗(b,A)的解。
命题2.2
对于任何 b ∈ R D , A ∈ R D × N {\bf b}\in \mathbb R^D,A\in \mathbb R^{D\times N} b∈RD,A∈RD×N并且 A ′ ∈ R D × N ′ A'\in \mathbb R^{D\times N'} A′∈RD×N′,令 Δ ( b , [ A , A ′ ] ) = [ c A ⊤ , c A ′ ⊤ ] ⊤ \Delta ({\bf b},[A,A'])=[c_A^\top,c_{A'}^\top]^\top Δ(b,[A,A′])=[cA⊤,cA′⊤]⊤。如果存在 A ′ A' A′中的列属于区域 Δ ( b , A ) \Delta ({\bf b},A) Δ(b,A),那么一定有 c A ′ ⊤ ≠ 0 c_{A'}^\top \neq 0 cA′⊤=0
这意味着,在字典中添加位于oracle区域内的新列时,弹性网络问题的解一定会改变。在下一节中,我们将描述一种有效的算法来解决弹性网问题(4),该算法基于解的几何结构和行为。
2.2 一种新的有效集算法
尽管弹性网络优化问题最近已被引入到子空间聚类中,但先前的工作并没有提供一种能够处理大规模数据集的有效算法。事实上,这种先前的工作使用的算法需要使用整个数据矩阵 A A A的计算的来解决弹性网问题。例如,使用加速近端梯度(APG)和线性化交替方向收缩法(LADM)。在这里,我们提出用一种比APG和LADM更有效的、能处理大规模数据集的有效集算法来解决弹性网络问题(4)。我们称我们的新算法1为ORacle-Guided-Elastic-netsolver,简称ORGEN。
算法1:ORGEN

ORGEN的基本思想是解决由有效集定义的一系列规模更小的子问题。令
T
k
T_k
Tk为迭代
k
k
k次的有效集,它记录了A列的index,那么下一次迭代的有效集
T
k
+
1
T_{k+1}
Tk+1只包含oracle region
Δ
(
b
,
A
T
k
)
\Delta({\bf b},A_{T_k})
Δ(b,ATk)中的
A
T
k
A_{T_k}
ATk列的索引。
A
T
k
A_{T_k}
ATk就是按照有效集index抽取列得到的子矩阵。如图三所示:

所有在单位球面上的点刻画了字典
A
A
A。在图a中,红色点集为第k次迭代的有效集,在图b中红色线段刻画了该字典内的oracle region,在图c中绿色的点为更新后的有效集,它落在了oracle region中。一旦有效集
T
k
+
1
T_{k+1}
Tk+1不再包含新的数据点(即
T
k
+
1
⊆
T
k
T_{k+1}\subseteq T_{k}
Tk+1⊆Tk时,此时
T
k
+
1
T_{k+1}
Tk+1就是
c
∗
(
b
,
A
)
c^*({\bf b},A)
c∗(b,A)的支撑集),迭代停止。
以下引理解释了ORGEN能够收敛。
引理2.1
算法1中的
T
k
+
1
⊈
T
k
T_{k+1}\nsubseteq T_{k}
Tk+1⊈Tk时,有:
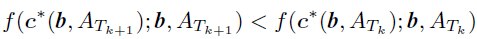
即当
T
k
+
1
T_{k+1}
Tk+1还在继续更新点的时候,一定能让更新后的公式(3)损失函数值更小
定理2.2
算法1一定能再有限次数的迭代后收敛到最优解 c ∗ ( b , A ) c^*({\bf b},A) c∗(b,A)。
这个结果来自引理2.1,因为它意味着一个活动集在更新过程中永远不会重复。由于只有有限多个不同的活动集,一定会在 T k + 1 ⊆ T k T_{k+1}\subseteq T_{k} Tk+1⊆Tk时算法1终止。接下来我们证明当 T k + 1 ⊆ T k T_{k+1}\subseteq T_{k} Tk+1⊆Tk时,解 c ∗ ( b , A ) c^*({\bf b},A) c∗(b,A)的元素都为非零。
ORGEN通过在算法1的第3步中通过解决一系列小规模的子问题来解决大规模问题。如果有效集
T
k
T_k
Tk很小,那么第3步是一个可以有效解决的小规模问题。但是,算法1中没有明确控制
T
k
T_k
Tk大小的过程。为了解决这个问题,我们提出了第5步的替代方案,即只添加少量与oracle点
δ
δ
δ最相关的点。具体来说:
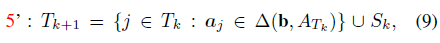
其中
S
k
S_k
Sk包含了:
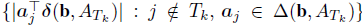
中最大的
n
n
n个元素的index。理想情况下,应选择
n
n
n以便
T
k
T_k
Tk的大小由一个预定值
N
m
a
x
N_{max}
Nmax限定,
N
m
a
x
N_{max}
Nmax表示步骤3中可以处理的最大的子问题的大小。如果选择的
N
m
a
x
N_{max}
Nmax足够大,使得公式(9)中并集的第二个集合
S
k
S_k
Sk非空,则我们的收敛结果仍然成立。
初始化
我们建议采用以下步骤计算初始有效集 T 0 T_0 T0。首先,令 λ = 0 λ=0 λ=0计算问题(4)的解,该解为闭式解,如果数据的环境维数D不是太大,则可以有效地计算。然后,对于某些预先指定的值 l l l, l l l个绝对值最大的解被添加到 T 0 T_0 T0中。实验结果表明该策略提高了算法1的收敛速度。
弹性网子空间聚类:EnSC
尽管已经引入了弹性网络用于子空间聚类,但这些工作并未提供保证子空间保持或连通性潜在改善的条件。在本节中,我们给出了保子空间的一致性,以及保持子空间和连通性之间平衡的条件。据我们所知,这是第一次建立这样的理论保证。
我们首先正式定义了子空间聚类问题。
问题3.1
令 X ∈ R D × N X\in \mathbb R^{D\times N} X∈RD×N为实值矩阵,它的列(也就是每个数据点)可以由 n n n个子空间 R D \mathbb R^D RD的并集,即 ⋃ l = 1 n S ℓ \bigcup_{l=1}^n\mathcal S_\ell ⋃l=1nSℓ刻画。其中,对于 ℓ ∈ { 1 , ⋯ , N } , \ell \in \{1,\cdots,N\}, ℓ∈{1,⋯,N},第 ℓ \ell ℓ个子空间的维度 d ℓ d_\ell dℓ满足 d ℓ < D d_\ell <D dℓ<D。子空间聚类的目标就是将 X X X的列分割到它们所的代表的子空间。
对于
X
=
[
x
1
,
⋯
,
x
N
]
X=[x_1,\cdots,x_N]
X=[x1,⋯,xN],假设每个
x
j
x_j
xj被单位标准化,那么根据公式(4),EnSC为每个
{
x
j
}
j
=
1
N
\{x_j\}_{j=1}^N
{xj}j=1N计算解
c
∗
(
x
j
,
X
−
j
)
c^*(x_j,X_{-j})
c∗(xj,X−j),即:
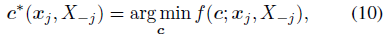
其中
X
−
j
X_{-j}
X−j指从
X
X
X中删除第
j
j
j列后的子矩阵。在本节中,我们主要关注如何得到
x
j
x_j
xj。我们假设对于某些
l
l
l,有
x
j
∈
S
ℓ
x_j\in \mathcal S_\ell
xj∈Sℓ,用
X
−
j
ℓ
X^\ell_{-j}
X−jℓ表示那些来自子空间
S
ℓ
\mathcal S_\ell
Sℓ的、除了
x
j
x_j
xj之外的列组成的子矩阵。
我们的一个目标是用各个元素的解 c ∗ ( x j , X − j ) c^*(x_j,X_{-j}) c∗(xj,X−j)去构建affinity矩阵。因此根据子空间保持性质的要求,我们希望非零的那些 c ∗ ( x j , X − j ) c^*(x_j,X_{-j}) c∗(xj,X−j)成为 X − j ℓ X^\ell_{-j} X−jℓ的子集,这样一来保证了其它零值的解能够使来自不同子空间的连接被断开。
另一方面,我们希望 X − j ℓ X^\ell_{-j} X−jℓ中的非零系数 c ∗ ( x j , X − j ) c^*(x_j,X_{-j}) c∗(xj,X−j)要稠密一些使得类内的连通性较好而不容易导致过分割。
因此这是一对冲突的目标增加:类内稠密很可能使得不同子空间也存在连接而无法保持子空间;希望不同子空间无联通势必会使得类内系数 c ∗ ( x j , X − j ) c^*(x_j,X_{-j}) c∗(xj,X−j)也变得系数而导致连通性差。
*注:事实上,即使每个子空间内连接良好,进一步改善子空间内的连通性仍然是有益的,因为它增强了后续步骤的谱聚类纠正affinity图中错误连接的能力。
在接下来的两节中,我们给出了子空间保持性和连通性之间折衷的几何解释,并提供了表示为子空间保持的充分条件。
3.1 子空间保持解 vs. 连通性解
我们的分析是建立在优化问题 m i n c f ( c ; x j , X − j ℓ ) min_cf(c;x_j,X_{−j}^\ell) mincf(c;xj,X−jℓ)上。注意,由于字典xj包含在S中,所以它的解是保子空间的平凡解。 然后将其他子空间中的所有点作为新添加到 X − j ℓ X_{-j}^\ell X−jℓ的列,并利用命题2.1和2.2,我们得到以下几何结果。
引理3.1
假设
x
j
∈
S
ℓ
x_j\in \mathcal S_\ell
xj∈Sℓ,那么向量
c
∗
(
x
j
,
X
−
j
)
c^*(x_j,X_{-j})
c∗(xj,X−j)是子空间保持的充要条件是:
对于所有
x
k
∉
S
ℓ
x_k\notin \mathcal S_\ell
xk∈/Sℓ,有
x
k
∉
Δ
(
x
j
,
X
−
j
ℓ
)
x_k\notin \Delta(x_j,X_{-j}^\ell)
xk∈/Δ(xj,X−jℓ)
我们说明了图4中引理3.1所示的几何结构,其中我们假设 S ℓ \mathcal S_\ell Sℓ是 R 3 \mathbb R^3 R3中的一个二维子空间。字典 X − j ℓ X_{−j}^\ell X−jℓ由平面中的蓝点表示,而oracle区域 Δ ( x j , X − j ℓ ) Δ(x_j,X{-j}^\ell) Δ(xj,X−jℓ)由两个红色圆盖表示。绿点都是字典里的其他点。引理3.1的几何解释是:当且仅当所有绿点位于红色区域之外, c ∗ ( x j , X − j ) c^*(x_j,X_{-j}) c∗(xj,X−j)是保持子空间的。

为了确保得到的解是保持子空间的,我们需要一个小较的oracle区域,而为了确保连通性,我们需要一个大的oracle区域。这些事实再次凸显了这两种属性之间的权衡。因此,当 λ λ λ从0增加到1时, ℓ 2 \ell_2 ℓ2的权重减小,预期oracle区域的大小将减小。定理3.1形式化了这一说法,但首先我们需要以下定义来描述数据在 X − j ℓ X_{-j}^\ell X−jℓ中的分布。
定义3.1 内半径
凸体 P \mathcal P P的内半径是内接 P \mathcal P P的最大 ℓ 2 \ell_2 ℓ2球的半径 r ( P ) r(\mathcal P) r(P)。
oracle区域的大小 Δ ( x j , X − j ℓ ) Δ(x_j,X_{-j}^\ell) Δ(xj,X−jℓ)由 λ ∣ ∣ δ ∣ ∣ 2 \frac{\lambda}{||\delta||_2} ∣∣δ∣∣2λ控制( δ \delta δ是 δ ( x j , X − j ℓ ) \delta(x_j,X_{-j}^\ell) δ(xj,X−jℓ)的缩写),正如图2所示的那样。
定理3.1
如果
x
j
∈
S
ℓ
x_j\in \mathcal S_\ell
xj∈Sℓ,那么:
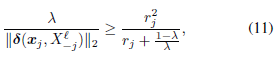
其中,
r
j
r_j
rj为
X
−
j
ℓ
X_{-j}^\ell
X−jℓ中数据点组成的对称凸球壳的内半径(定义如3.1),即:
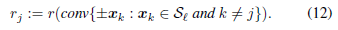
当
λ
=
0
λ=0
λ=0时,我们将公式(11)的右侧定义为0。
上述定理允许我们确定oracle区域大小的上界。这是因为 λ ∣ ∣ δ ∣ ∣ 2 \frac{\lambda}{||\delta||_2} ∣∣δ∣∣2λ大小的下限意味着oracle区域大小的上限(参见公式(8)和图2)。此外,公式(11)的右侧在 [ 0 , r j ) [0,r_j) [0,rj)范围内,并且随着 λ λ λ的增加单调增加。因此,它提供了oracle区域面积的上限,该上限随着 λ λ λ的增加而减小。这强调了子空间保持性和连通性之间的权衡是由 λ λ λ控制的。
remark 3.1
我们已经知道
λ
∣
∣
δ
∣
∣
2
\frac{\lambda}{||\delta||_2}
∣∣δ∣∣2λ的下限是
λ
\lambda
λ的增函数,如果
λ
∣
∣
δ
∣
∣
2
\frac{\lambda}{||\delta||_2}
∣∣δ∣∣2λ本身是
λ
\lambda
λ的增函数就更好了。然而并不行。以数据点
x
j
=
[
0.22
,
0.72
,
0.66
]
⊤
x_j=[0.22,0.72,0.66]^\top
xj=[0.22,0.72,0.66]⊤为例:
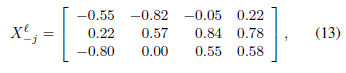
参数
γ
=
10
\gamma =10
γ=10,那么
λ
=
0.88
\lambda=0.88
λ=0.88时的
λ
∣
∣
δ
∣
∣
2
\frac{\lambda}{||\delta||_2}
∣∣δ∣∣2λ大于
λ
=
0.95
\lambda=0.95
λ=0.95时的
λ
∣
∣
δ
∣
∣
2
\frac{\lambda}{||\delta||_2}
∣∣δ∣∣2λ
3.2 子空间保持解的条件
将引理3.1中的几何分析与定理3.1中的oracle区域大小的界结合起来,得到解是子空间保持的充分条件。
定理3.2
令
x
j
∈
S
ℓ
,
δ
j
=
δ
(
x
j
,
X
−
j
ℓ
)
x_j\in \mathcal S_\ell, \delta_j=\delta(x_j,X_{-j}^\ell)
xj∈Sℓ,δj=δ(xj,X−jℓ)为oracle点,
r
j
r_j
rj为
X
−
j
ℓ
X_{-j}^\ell
X−jℓ由公式(12)得到的内半径,那么当满足一下不等式时,解
c
∗
(
x
j
,
X
−
j
)
c^*(x_j,X_{-j})
c∗(xj,X−j)是子空间保持的:(
μ
\mu
μ的定义参见公式7)
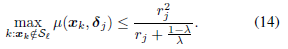
注意,在定理3.2中,根据 δ ( x j , X − j ℓ ) \delta(x_j,X_{-j}^\ell) δ(xj,X−jℓ)的定义, δ j δ_j δj是由位于子空间 S ℓ \mathcal S_\ell Sℓ中的 X − j ℓ X_{-j}^\ell X−jℓ确定的。因此公式(14)的左侧描述了在 S ℓ \mathcal S_\ell Sℓ中的oracle点和 S ℓ \mathcal S_\ell Sℓ之外的点集的分离程度。而在公式的右侧, r j r_j rj描述了 X − j ℓ X_{-j}^\ell X−jℓ中点的分布。特别地,当点在 S ℓ S_\ell Sℓ内分布良好且不向任何方向倾斜时, r j r_j rj较大。最后,请注意公式的右侧是 λ λ λ的递增函数,这表明如果相对于 ℓ 2 \ell_2 ℓ2,在 ℓ 1 \ell_1 ℓ1上放置更多的权重,则解更有可能是子空间保持的。
定理3.2与SSC给出子空间保持解的充分条件密切相关( λ = 1 λ=1 λ=1的情况)。具体来说,SSC给出子空间保持解的条件是: m a x k : x k ∉ S ℓ μ ( x k , δ j ) < r j max_{k:x_k\notin \mathcal S_\ell} μ(x_k,δ_j)<r_j maxk:xk∈/Sℓμ(xk,δj)<rj。我们可以观察到 λ → 1 λ→ 1 λ→1时公式(14)退化为SSC的条件。
定理3.2中的结果是下面更一般结果(定理3.3)的特例。
定理3.3
令
x
j
∈
S
ℓ
,
δ
j
=
δ
(
x
j
,
X
−
j
ℓ
)
x_j\in \mathcal S_\ell, \delta_j=\delta(x_j,X_{-j}^\ell)
xj∈Sℓ,δj=δ(xj,X−jℓ)为oracle点,
κ
=
m
a
x
k
≠
j
,
x
k
∉
S
ℓ
μ
(
x
k
,
δ
j
)
κ=max_{k\neq j,x_k\notin \mathcal S_\ell} μ(x_k,δ_j)
κ=maxk=j,xk∈/Sℓμ(xk,δj)表示
δ
j
\delta_j
δj和它在
X
−
j
ℓ
X_{-j}^\ell
X−jℓ中的最近邻的相干性(coherence)。那么定理3.2的充要条件可以更一般地写作:
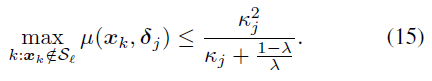
这个结果与定理3.2的唯一区别是用
κ
j
κ_j
κj代替
r
j
r_j
rj来刻画xj中点的分布。在其他文献中表明
r
j
≤
κ
j
r_j≤ κ_j
rj≤κj,这使得定理3.3比定理3.2更具一般性。几何上,
r
j
r_j
rj较大的条件是:子空间
S
ℓ
\mathcal S_\ell
Sℓ被
X
−
j
ℓ
X_{-j}^\ell
X−jℓ很好地覆盖;而
κ
j
κ_j
κj较大的条件是最靠近oracle点
δ
j
δ_j
δj的最近邻被很好地覆盖,即:
X
−
j
ℓ
X_{-j}^\ell
X−jℓ中有一个点十分接近
δ
j
\delta_j
δj。因此,定理3.2中的条件要求每个子空间都被数据全局覆盖,而定理3.3中的条件允许数据存在bias,只要求局部区域被覆盖。另外,当数据点的所属已知时,可以检查条件(15)。这一优势使我们能够检查条件(15)的紧确性。相比之下,条件(14)和先前关于SSC的工作使用了内半径
r
j
r_j
rj,这通常是NP-hard的计算问题。
4. 实验
在人工数据上的ORGEN
我们进行了综合实验来说明所提出的算法ORGEN的计算效率。与三种流行的求解方法进行对比:正则化特征符号搜索(RFSS)是一种有效集类型的方法;在稀疏建模软件SPAMS中实现LARS算法的LASSO版本;以及用于稀疏重建的梯度投影(GPSR)算法。这三个求解器用于解决ORGEN步骤3中的子问题,从而得到ORGEN的三个实现。为了进行比较,我们还将这三个求解器用于独立计算。
在所有的实验中,向量KaTeX parse error: Expected 'EOF', got '}' at position 6: \bf b}̲和A 的 列 都 是 在 的列都是在 的列都是在\mathbb R^{100}$的单位球面上独立均匀地随机生成的。结果是50次试验的平均值。
在第一个实验中,我们通过改变N检验了ORGEN的有效集缩放行为;结果如图5(a)所示。我们可以看到,我们的有效集方案提高了所有三个解算器的计算效率。此外,随着N的增加,改善变得更加显著。
接下来,我们测试了ORGEN对于控制子空间保持性和连通性之间折衷的参数λ的不同值的性能;运行时间和稀疏度分别如图5(b)和5(c)所示。spam的性能没有报道,因为即使λ的值很小,spam的性能也很差。对于所有方法,计算效率随着λ变小而降低。对于ORGEN的两个版本,这是符合预期的,因为随着λ变小,解变得更稠密(见图5(c))。因此,有效集变得更大,这直接导致步骤3中的子问题更大、更耗时。



EnSC在真实数据集上的表现
略。在EnSC+ORGEN时获得最好的效果。
6 结论
我们研究了弹性网正则化(即 ℓ 1 \ell_1 ℓ1和 ℓ 1 \ell_1 ℓ1)用于scalable和provable的子空间聚类。特别地,我们提出了一种有效集算法,该算法利用弹性网解的几何结构,有效地解决了弹性网正则化子问题。然后,我们给出了基于几何解释的理论证明,在子空间保持性和连通性之间进行折衷,以确保通过弹性网络进行子空间聚类的正确性。大量实验证明,我们提出的主动集方法达到了最先进的聚类精度,能够处理大规模数据集。






















 374
374











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








