有效集法介绍（Active Set Method）（转）

有效集法介绍（Active Set Method）（转）

单纯性法（Simplex Method）是“线性规划之父”George Dantzig 最著名的成果，也是求解线性规划最有力的算法之一。而这一算法在求解二次规划（Quadratic Programming, QP）时的升级版就是有效集法（Active Set Method, ASM）。这两种算法的特点都是迭代点会循着约束边界前进，直到达到问题的最优点。本文对用于求解 QP 命题的 Primal ASM 算法作以介绍，主要内容的来源是 Nocedal 等人 2006 年的著作 Numerical Optimization 第二版。

有效集（Active Set）

要说有效集法，首先要说说什么是有效集。有效集是指那些在最优点有效（active）的不等式约束所组成的集合。例如，考虑二次函数 

min.fs.t.xy=x2+y2+2x+y≥0≥−1

函数的等高线及两个约束的图像如下： 

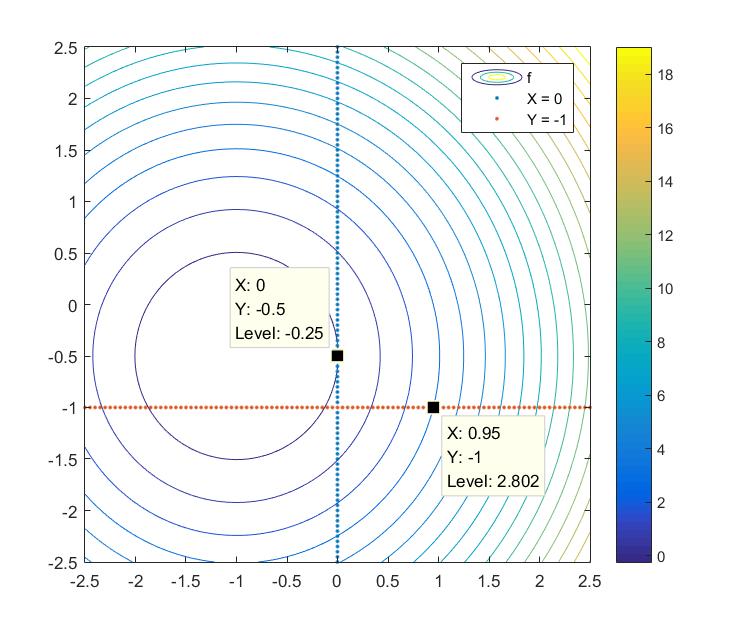
通过计算或者从图上可以看出，当没有约束时，目标函数的最小值在  (−1,−0.5)  处取得。当考虑上述的两条约束时，目标函数的最小值在  (0,−0.5)  处取得。这个时候在最优点处，约束  x≥0  中的等号被激活，这条约束就被称为有效约束（active constraint）。如果我们记两条约束的编号为  1  和  2 ，那么在最优点处的有效集就可以记为 

A∗={1}

而如果原命题中  y≥−1  这条约束改为  y≥−0.5  ，即要求解的优化命题变为 

min.fs.t.xy=x2+y2+2x+y≥0≥−0.5

函数的等高线及两个约束的图像如下： 

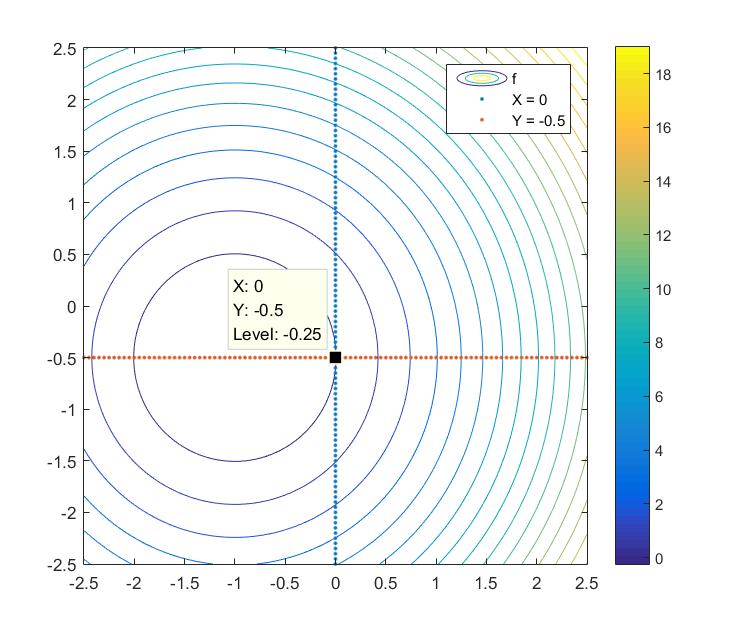
此时优化命题的解仍然是  (0,−0.5)  ，但在最优点处两条约束均被激活，即此时的有效集可以记为 

A∗={1,2}

有效集法

从上面可以看出，如果我们能提前知道在最优点处有效的约束，那我们就可以把那些未有效的不等式约束剔除掉并把原命题转化成更易求解的等式约束命题。然而，在求解之前我们往往对最优点处的有效约束知之甚少。因此如何找到最优点处的有效约束也就是有效集法的主要工作。另外在这里要提一点，其实在一些应用中，我们需要求解一系列类似的 QP 命题，这个时候我们往往对最优点处的有效约束有一个初始猜测，因此通过这种方式可以实现算法的热启动（Warm Start），从而加速算法的收敛。下面我们正式开始介绍 ASM 的理论。我们考虑的是带有不等式约束的凸二次规划命题： 

minxq(x)subject toaTix=12xTGx+xTc≥bi,i∈I

在 ASM 中，我们会构造一个工作集（Working Set），与有效集类似，工作集也是有效约束的集合，但只是我们认为在某次迭代中有效约束的集合，它可能与最优点处的有效集相同，也有可能不同。如果相同，我们可以通过计算对偶变量  λ  了解到此时已经是最优点从而退出迭代。如果不同，我们会对工作集进行更新，从现有工作集中删除一条约束或者增加一条新的约束到工作集中。因为工作集是随着迭代而改变的，因此记工作集为  Wk  。

在第  k  次迭代开始时，我们首先检查当前的迭代点  xk  是否是当前工作集  Wk  下的最优点。如果不是，我们就通过求解一个等式约束的 QP 命题来得到一个前进方向  p  ，在计算  p  的时候，我只关注  Wk  中的等式约束而忽略原命题的其他约束。为了便于计算，我们定义 

p=x−xk,gk=Gxk+c

把上面的定义代入原命题有： 

q(x)=q(xk+p)=12pTGp+gTkp+ρk

其中  ρk=12xTkGxk+xTkc  在这里可以看作是常数因此可以从上面的优化命题中去掉。因此我们可以写出如下所示的在第  k  次迭代需要求解的 QP 子命题： 

minqsubject to12pTGp+gTkpaTip=0,i∈Wk

我们记上面的命题求解得到的最优解为  pk ，首先假定求解得到的  pk  不为0 ∗ 。即我们有了一个方向使得沿着这个方向目标函数会下降，然后我们需要确定一个步长  αk  来决定走多远。如果  xk+pk  对于所有原命题的约束都是可行的，那么此时的  αk=1 ，否则  αk  则是一个小于1的正数。定义步长  αk  之后我们就可以得到迭代点更新的式子： 

xk+1=xk+αkpk

关于步长  αk  的计算，我们有如下的分析。其实，步长的计算主要就是要保证新的迭代点不要违反原命题的约束，那么在工作集  Wk  内的约束就不用担心了，因为在求解  pk  的过程中就已经保证了工作集内的约束必须得到满足。那么对于非工作集中的约束  i∉Wk ，我们首先判断  aTipk  的符号，如果  aTipk≥0  ，那么通过分析可知只要步长  αk  大于0，则该约束一定可以满足，因此我们需要关注的主要就是  aTipk<0  的那些约束。为了保证原命题中的约束  aTi(xk+αkpk)≥bi  能够满足，我们需要使得  αk  满足 

αk≤bi−aTixkaTipk

因此，我们可以把计算  αk  的方法显式地写出来： 

αk=min(1,mini∉Wk,aTipk<0bi−aTixkaTipk)

要注意的是，虽然我们这里的确把  αk  显式地表示出来，但仔细看就会发现求解  αk  其实还是一个逐条约束去检查的过程。比如对于我们从  αk=1  开始，逐条约束开始判断，首先判断如果  aTipk≥0  则直接跳到一条约束，否则可以判断  αk  与  bi−aTixkaTipk  的大小，如果前者小于后者，那么没问题可以去检查下一条约束，否则直接令  αk  取值为后者。以我自己的经验，当原命题的约束个数较多时，计算步长  αk  往往是一个比较耗时的环节。如果能有什么好办法可以削减这部分的计算量，那么对于 QP 的加速求解将会是很有益的工作。

当我们在计算  αk  的时候，每条约束都会对应一个不违反其约束的最小的  αk  的值，而且在最小的  αk  就是这次迭代的步长值  αk  ，而这条约束就被称为 blocking constraint（如果  αk=1  且没有新的约束在下一步迭代点处激活，那么此次迭代没有 blocking constraint）。注意，也有可能出现  αk=0  的情况，这是因为在当前迭代点处有其他的有效约束没有被添加到工作集中。如果  αk<1 ， 也就是说下降方向  pk  被某条不在工作集  Wk  内的约束阻拦住了。因此我们可以通过将这条约束添加到工作集的方法来构造新的工作集  Wk+1  。

通过上面的方法我们可以持续地向工作集内添加有效约束，直到在某次迭代中我们发现当前的迭代点已经是当期工作集下的最优点。这种情况很容易判断，因为此时计算出来的  pk=0 。接下来我们就要验证当前的迭代点是不是原命题的最优点，验证的方法就是判断工作集内的约束对应的对偶变量  λ  是否都大于等于 0，如果满足这一点，那么所有的 KKT 条件都成立，可以退出迭代并给出原命题的最优解（关于这部分的推导，详细内容请见原书的 16.5 节）。 λ  的计算由下式给出 

∑i∈W^aiλi^=g=Gx^+c

如果通过上式计算出来的有一个或者多个  λ^i  的值小于 0。那么就表明通过去掉工作集的某一条或几条约束，目标函数值可以进一步下降。因此我们会从对应的  λ^i  值小于 0 的约束中选择一条，将其从工作集  Wk  中剔除从而构造出新的工作集  Wk+1  。如果有多于一条的可选约束，那么不同的剔除方法会遵循不同原则，我们在这里不加更多说明地遵循去除对应  λ^i  值最小（绝对值最大）的那条约束。

基于上面的讨论，我们可以得到一个 Primal 的 ASM 的算法，具体的算法可见原书 Algorithm 16.3，这里我们给出一个算法的流程图。

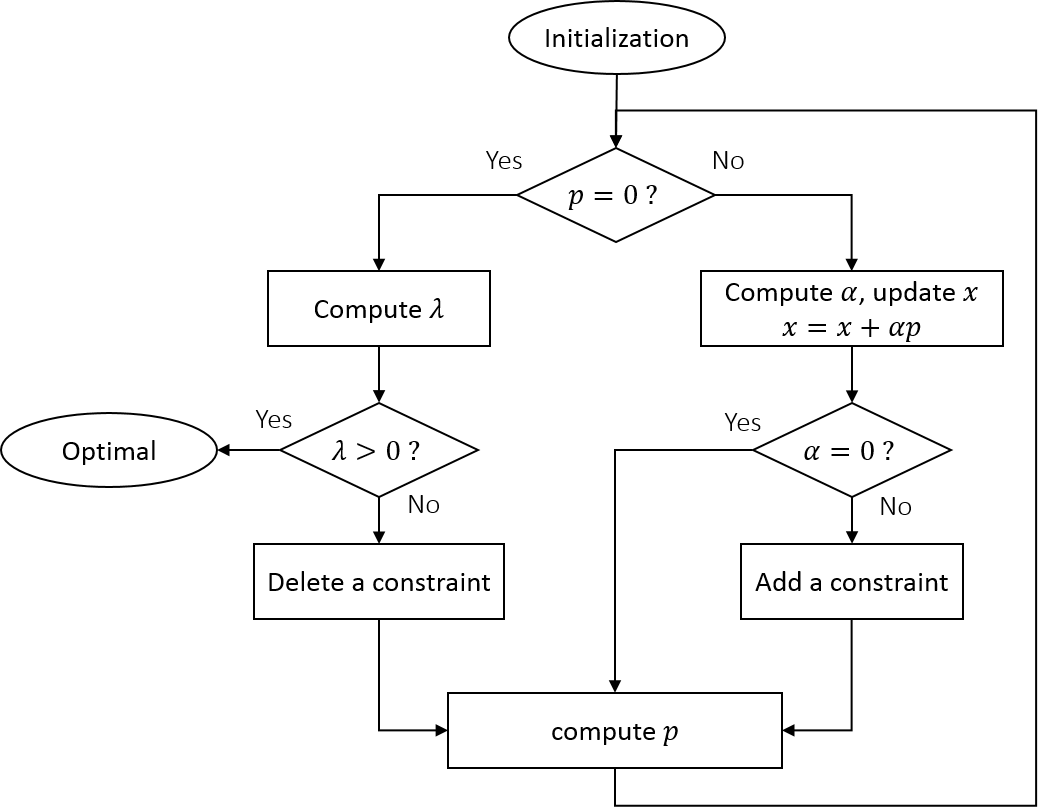
这里要注意，Primal ASM 算法的迭代点都是在可行域内或者可行域的边界上移动，这样的好处是即使你提前终止迭代，那么算法得到的也是一个可行解（Dual 的算法往往不能保证这一点）。而这样的缺点则是在算法启动是需要我们给定一个可行的初始点，而求解这样一个可行的初始点往往也不是一件简单的事情。现在的一种方法是通过一个 Phase I 的过程来得到这样一个可行的初始点，也就是求解一个只有约束的线性规划命题。而初始的工作集往往可以取为空集。

举例

我们用下面这个二维的例子来说明 ASM 算法的过程。 

minxq(x)=(x1−1)2+(x2−2.5)2ssubject tox1−2x2+2−x1−2x2+6−x1+2x2+2x1x2≥0,≥0,≥0,≥0,≥0.

示意图如下： 

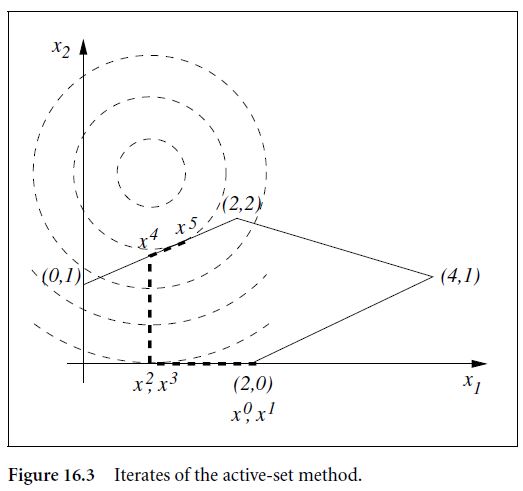
假设此时迭代初始点为  x0=(2,0)T ，初始的工作集为  W0={3,5}  。注意此时初始工作可以只有约束 3 或 5，也可以是空集，这里我们只是举一个  W0={3,5}  的例子。当这两条约束点都激活时，迭代点  x0=(2,0)  显然是当前工作集下的最优点，即  p0=0 。因此我们有  x1=(2,0)T 。当  p0=0  时，我们需要检查对偶变量  λ  的符号。计算可以得到  (λ^3,λ^5)=(−2,−1) 。因为不是所有的对偶变量都是正值，说明当前迭代点不是最优点，因此我们需要从工作集中删除一条约束，这里我们选择删除对应的对偶变量的绝对值最大的值所对应的约束，即第 3 条约束。

即此时工作集内只有第 5 条约束，  W1={5}  。在当前的工作集下计算得到的  p1=(−1,0)T  。因为在前进的路上没有 blocking constraint 的阻碍，因此计算得到的步长  α1=1 。同时我们可以得到新的迭代点  x2=(1,0)T 。

因为步长  α1=1 ，因此我们在工作集不变的情况下，即  W2={5} ，再求解一次等式约束命题，此时我们会得到前进方向  p2=0 ，因此更新后的迭代点为  x3=(1,0)T 。因此我们去检查各个对偶变量的正负号，通过计算可得  λ^5=−5 ，说明当前点不是最优点，同时我们将约束 5 从工作集中删除。

此时工作集为空集，即  W3=∅ 。此时求解下降方向就相当于在求解一个无约束命题，从图中可以看出，下降方向为  p3=(0,2.5) 。然而此时，在下降的方向上有 blocking constraint 的存在，因此计算得到的步长为  α3=0.6 ，同时我们得到新的迭代点为  x4=(1,1.5)T ，同时我们将 blocking constraint 添加到工作集中得到更新后的工作集为  W4={1} 。

此时进入下一次迭代，求解得到的下降方向为  p4=(0.4,0.2) 。并且在前进的方向上没有 blocking constraint，因此求得的步长为 1 。得到的新的迭代点为  x5=(1.4,1.7)T 。因为步长为 1，因此我们在不改变工作集的情况下再计算一次下降方向，得到  p5=0 ，此时我们检查对偶变量的值，发现  λ^1=0.8  是正值，说明当前的迭代点已经是最优点。因此我们退出迭代，并得到问题的最优解  x∗=(1.4,1.7)T 。

通过上面这张图，我们可以较为清楚地了解 ASM 算法的计算流程。

后记

最后要提一点，关于算法的收敛性，原书中的定理 16.6 证明了，只要每次迭代的前进方向  pk  是从上文所提到的等式约束命题求解出来的，那么就可以证明，目标函数的值沿着该方向一定会减少，而这就保证了ASM 算法的迭代可以在有限次数内终止，从而证明的算法的收敛性。那么其实算法的收敛性不是靠在添加约束和删除约束的对约束的选择来保证的，那就说明，在具体的应用中我们可以根据情况选择添加和删除约束的策略，从而实现算法的快速收敛。

∗  所谓判断一个向量是否为0在代码实现时是一个很微妙的问题，根据我自己的经验。当采用 double 精度实现时，如果所有元素的绝对值小于  10−6  就可以认为  pk  是 0，而对于 float 精度的实现，这一阈值约为  10−3 。