【CVPR 2021】剪枝篇（一）：Network Pruning via Performance Maximization

论文地址：

https://openaccess.thecvf.com/content/CVPR2021/papers/Gao_Network_Pruning_via_Performance_Maximization_CVPR_2021_paper.pdf

主要问题：

通道剪枝是一种比较通用而且效果较好的模型压缩方法，通过修剪权重和激活的通道来获得一个小的子网络

为了找到这样的子网络，许多现有的信道剪枝方法都使用分类损失作为指导

然而修剪过的子网络并不一定具有较高的精度和低分类损失，而这往往是由于损失度量不匹配造成的（作者在后面的实验中也证明了性能预测网络的梯度和分类损失有不同的方向）

因此在本文中，作者首先考虑了剪枝的损失度量不匹配问题，并提出了一种新的卷积神经网络的通道剪枝方法，用来直接最大化子网络的性能（即精度）

主要思路：

具体地说就是，我们训练一个独立的神经网络来预测子网络的性能，然后最大化网络的输出作为指导剪枝

并且在这个剪枝过程中，我们可以直接使用子网络和小批量精度作为样本来训练性能预测网络（是否想到了强化学习）

但是有效地训练这种性能预测网络往往是比较困难的，可能会面临灾难性遗忘和子网络分布不平衡的问题

为了解决这个问题，作者使用一个事件记忆模块来沿着剪枝轨迹收集样本

直接使用这些样本是有问题的，因为这些样本的准确性分布远不均匀，但是这个问题可以通过重新采样这些样本来解决（跟DQN里面经验池很像）

利用上述技术，性能预测网络在剪枝过程中进行了增量训练

在性能预测网络访问足够的样本并足够精确后，放到剪枝过程中，为通道剪枝提供额外的监督

由于性能预测网络的训练和剪枝工作同时进行，因此没有额外的成本

此外作者并没有放弃分类损失（通常是交叉熵损失），并且参考多目标学习的理念，在最终损失函数的定义中同时考虑了分类损失和性能最大化

这背后的基本原理是，分类损失和性能最大化都为修剪提供了有用但不同的信息，并且合并它们将会得到更好的结果

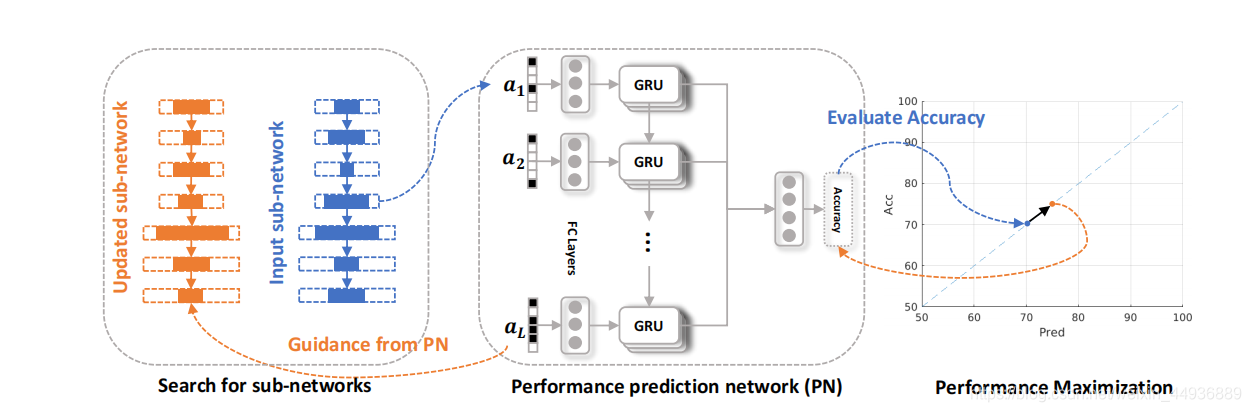
具体实现：

基本符号：

在CNN中，第 $i$ 层的特征图可以表示为 $F_i\in R^{C_i\times W_i\times H_i},i=1,...,L$，其中 $C_i$ 是通道数，$L$ 是层数

用 $1(\cdot )$ 表示指标函数， $\odot$ 表示点积

子网络生成：

正如我们前面所讨论的，直接采样子网络通常会产生琐碎的结果，特别是当剪枝率很高的时候

为了训练一个针对信道剪枝的性能预测网络，我们不需要遍历所有的子网络

假设原始模型的 FLOPs 为 $T_{total}$，剪枝率为$p$，我们对从$p{T}_{total}$ 到$T_{total}$ 的子网络很感兴趣

我们首先丢弃 FLOPs 低于 $p{T}_{total}$ 的子网络，因为它们不满足 FLOPs 约束

因此，我们更喜欢生成具有特定 FLOPs 的有意义的子网络作为性能预测网络的训练样本

我们开始先通过将原始模型修剪到目标 FLOPs $p{T}_{total}$ 来生成这些子网络

为了实现这一点，我们首先引入了基本的可微剪枝算法

我们使用可微门来描述一个通道，对于第 $i$ 层，门的定义为：

$o_i=1/(1+e^{-(w_i+s)/\tau })$

其中 $1/(1+e^{-(w_i+s)/\tau })$ 就是 sigmoid 函数，$o_i\in R^{C_i}$ 并且 $o_i\in [0,1]$,

$w_i\in R^{C_i}$ 是门控单元可学习的参数，$s$ 是从 Gumbel 分布的采样，$s\in Gumbel(0,1)$，$\tau$ 是来控制锐度的超参数

这里的 $o_i$ 是连续的，用来精确地生成子网络

然后我们进一步将其规范到 $0$ 或 $1$：

$a_i=1_{o_i>\frac{1}{2}}(o_i)$

其中 a i ∈ { 0 , 1 } C i a_i\in \{0,1\}^{C_i} ai​∈{0,1}Ci​

由于指示函数 $1(\cdot )$ 不可微，作者使用了直通式估计器（straight-through estimator）来计算梯度

上述两个等式中的可微分门则使用 Gumbel-Solftmax 算法来近似伯努利分布（虽然有近似伯努利分布，但作者发现它们的差异也并不显著）

为了实现最终的剪枝，我们将门控单元应用到特征图上：

$\widehat{F_i}=a_i\odot F_i$

其中 $a_i$ 被扩充到了 $F_i$ 的大小

这样整个剪纸过程的优化目标就可以写作：

${\min }_{w}L(f(x;a,\Theta ,y)+R(T(a),p{T}_{total}))$

其中 $w$ 包括了所有门控单元的可学习参数，$a$ 是用于表示 CNN 模型结构的向量，$a=cat(a_1,...,a_i,...,a_L)$，$T(a)$ 是由 $a$ 定义的子网络的 FLOPs ，$x,y$ 分别是输入图片及其标签，$f(\cdot ;a,\Theta )$ 是由 $\Theta$ 参数化的 CNN 模型（其结构由 $a$ 定义），$R(T(a),p{T}_{total})=log(max(T(a),p{T}_{total})/p{T}_{total})$ 是推动子网络到达目标 FLOPs 的正则化项

在上述等式的优化过程中会生成许多具有不同结构 $a$ 的子网络

假设精度 $q$ 是基于给定的小批量计算的，我们就可以得到一对代表一个子网络及其精度的样本$(a,q)$

性能预测网络：

一旦我们获得了样本$(a,q)$，我们就可以训练一个神经网络来预测给定子网络结构的性能

我们首先定义了性能预测网络：$q_{pred}=PN(a)$

$PN(\cdot )$ 就是所提出的性能预测网络

然后使用 sigmoid 函数作为输出激活，因此 $q_{pred}$ 在 $0$ 到 $1$ 的范围之间

性能预测网络由全连接层和 GRU 组成。简而言之，全连接的层将每个层的结构向量转换为一个紧凑的向量表示形式，并使用GRU来连接不同的层

作者使用GRU，是考虑到 $a_{i-1}$ 和 $a_i$ 有隐式的依赖性，因此 GRU 可能会使得性能预测网络有可能捕获子网络中复杂的交互

PN优化是一个回归问题，作者采用平均绝对误差损失（MAE）进行优化：

$mi{n}_{w_p}{L}_p=|q-PN(a)|$

其中 $w_p$ 是性能预测网络的参数

事件记忆模块：

作者做的这项工作的早期版本直接利用当前迭代的子网络来训练性能预测网络

然而，作者发现它只会恶化剪枝过程，这是因为性能预测网络很难预测早期子网络，这种现象被称为灾难性遗忘（catastrophic forgetting）

为了克服这个问题，我们需要定期回放以前的子网络

因此作者进一步提出了一个事件记忆模块（Episodic Memory Module）来记忆早期的子网络

事件记忆定义为 $EM=(A,Q)$，其中 $A\in R^{m\times K},Q\in R^K$，$m$ 是向量 $a$ 的长度，$K$ 是当前 EM 的大小

当我们向 EM 添加一个子网络时，$K$ 自动加 $1$，并且 $K$ 小于预先定义的最大 EM 容量 $K_{max}$

但是正如前面提到的，小批量精度不是一个很好的估计精度；而另一方面，如果我们使用整个训练数据集来计算精度，计算成本就太过昂贵

为了利用效率和精度，我们每 $c$ 次迭代收集子网络和相应的小批量精度的均值，以构建一个增强的子网络表示：

$\overline{a}=1_{a>\frac{1}{2}}(\frac{1}{c}{\sum }_{i=1}^c{a}_i),\overline{q}=\frac{1}{c}{\sum }_{i=1}^c{q}_i$

注意如果 $c$ 太大，那么上面的参数是无效的，导致增强的表示是无用的

此外在收集子网络时，我们不比计算梯度

假设我们在 EM 模块中已经有 $K$ 个子网，那么 EM 就可以通过以下方式更新：

$$P_{r-j}=\{\begin{array}{ll}{A}_i=\overline{a},i=\underset{i}{\mathrm{argmin}}|Q_i-\overline{q}|& ifK=K_{max},\\ A_{K+1}=\overline{a}& otherwise\end{array}$$

也就是说当 $K=K_{max}$ 时，我们将替换掉跟当前样本精度最相近的样本

事实上，在修剪过程中，大多数子网络在满足目标 FLOPS 后都具有相似的性能

因此，我们将使用 $K_{max}$ 来鼓励子网络的多样性

精度分布不平衡：

在剪枝过程中，作者绘制了子网络精度的经验分布，发现精度集中在84左右：

为了防止性能预测网络提供没有价值的解决方案，并使其收敛速度更快，作者提出可以根据子网络的准确性进行重新采样

即将所有的子网络按照 $Q$ 的等差 $\frac{1}{N-1}(max(Q)-min(Q))$ 分为 $N$ 个组

然后我们对每一组的子网络进行计数，并根据其计数的倒数对其进行重新抽样

这就相当于创建 $N$ 个伪类并进行重新采样

性能最大化算法：

在拥有了一个相对靠谱的性能预测网络后，我们开始最大限度地提高搜索更好的子网络的性能

子网络的性能可以表示为 $PN(a)$，因此我们可以最大化 $PN(a)$ 作为精度的估值

${\max }_{w}PN(a)$ 跟 ${\min }_w\frac{1}{PN(a)}$ 是等价的，因此为了使得训练更稳定，我们优化目标就可以写作：${\min }_{w}log(\frac{1}{PN(a)})$

这样总的优化目标就可以表示为：

$$\begin{array}{rl}\underset{w}{\min }J(w)=& L(f(x;a,\Theta ),y)+\gamma (K,L_P)\cdot log(\frac{1}{PN(a)})\\ & +\lambda R(T(a),p{T}_{total})\end{array}$$

其中 $\gamma (K,L_P)$ 是一个反映性能预测网络置信度的函数，被用来自动控制 $log(\frac{1}{PN(a)})$ 的量级，$\lambda$ 被用来控制正则化的量级

$\gamma (K,L_P)$ 定义为：$\gamma (K,L_P)=1_{K\ge \frac{K_{max}}{4}}(K)\cdot (1-L_p{)}^2$，范围为 $[0,1]$

通常来说更低的 $L_p$ 表示 $PN(\cdot )$ 具有更高的置信度，但是 $PN$ 的训练是一项增量学习任务，在 $PN$ 能够访问足够的样本之前，$L_p$ 可能不是很可靠

虽然存在损失-度量不匹配的问题，但来自损失函数和性能最大化的信息仍有一些重叠

由于我们已经使用了分类损失，因此希望从性能最大化中获得独特的信息

为了实现这一点，我们使梯度彼此正交

假设 $g_L^i=\frac{\partial L}{\partial w_i}$ 表示第 $i$ 层的分类损失的梯度，$g_p^i=\frac{\partial log(\frac{1}{PN(a)})}{\partial w_i}$ 是性能最大化损失的梯度

这两个项的修正梯度为：

$g^i=g_L^i+{\hat{g}}_p^i$

其中 $g_p^i$ 可以分解成两部分：$g_p^i={\hat{g}}_p^i+{\overline{g}}_p^i$，其中 ${\hat{g}}_p^i\perp g_L^i$ 并且 ${\overline{g}}_p^i$ 跟 $g_L^i$ 方向相同

作者也给出了整个算法的伪代码：

实验结果：