神经网络学习笔记（9）——神经网络中的线性变换

在上次的学习笔记中说到，线性代数是神经网络所需要的的数学基础，而且上次复习了线性空间相关知识，本章将探讨在神经网络中的线性变换。 在之前的学习笔记中说到的输入向量与权值矩阵相乘是执行神经网络的重要操作，该操作就是线性变换的一个具体实例。

1.线性变换
首先定义变换的概念。
变换 一个变换有三个部分
（1）一个被称为定义域的元素集合X={xi}；
（2）一个被称为值域的元素集合Y={yi}；
（3）一个将每个xi∈X和一个元素yi∈Y相联系的规则；
线性变换 一个变换A是线性的，如果
（1）对所有的x1，x2∈X，A（x1+x2）=A(x1)+A(x2);
（2）对所有的x∈X和a∈R，A（ax）=aA（x）
假设某个变换A是二维空间中将一个向量旋转θ角度（如图1所示）图2.3 表示该旋转变换满足线性变换定义中的条件1， 图4 表示旋转变换满足线性变换定义中的条件2.由此可以看出，旋转变换是一个线性变化。

图一

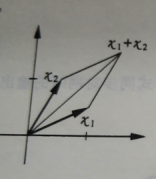
图二

图三

图四