滤波器相关知识

予米

已于 2023-08-01 16:53:53 修改

阅读量1.1k

点赞数 10

文章标签：笔记

于 2023-04-13 17:10:29 首次发布

本文链接：https://blog.csdn.net/weixin_44960102/article/details/130134668

版权

1. 术语 term

弛豫 — 如果在 $n_{0}$ 之前没有激励，那么初始条件 $y(n_{0} - 1)=0$ 。在这种情况下，我们说该系统是起始弛豫的。
因果系统与非因果系统 — 如果一个系统在任意时刻n的输出[即 $y (n)$ ]仅依赖于当前和过去的输入[即 $x (n), x (n - 1), x (n - 2), ...$ ]，而与将来的输入[即 $x (n + 1), x (n + 2), ...$ ]无关，那么这个系统就称为是因果的。数学上，因果系统的输出应该满足如下形式的方程：
$y (n) = F [x (n), x (n - 1), x (n - 2), ...]$
区别在于，是否和将来的输入有关。

递归与非递归 — 如果y(n)依赖于先前的输出值[即 $y (n - 1), y (n - 2), ...$ ]、当前和过去的输入[即 $x (n), x (n - 1), x (n - 2), ...$ ]，则这个系统是递归的。
$y (n) = F [y (n - 1), y (n - 2), ..., y (n - N), x (n), x (n - 1), ..., x (n - M)]$
相反，如果y(n)仅仅依赖于当前和过去的输入，那么
$y (n) = F [x (n), x (n - 1), ..., x (n - M)]$
这样的系统称为非递归的。
区别在于，是否依赖于过去的输出值。

（作者注：因果系统可以是递归的，也可以是非递归的。反过来，递归系统，可以是因果的也可以是非因果的）

3dB
分贝（Decibel）是一个单位，它是用以10为底的对数来表示一个物理量的值相对于另一个被定为参考值的相对大小（而不是绝对值量）。以符号dB表示。
（dB这种单位，其中"Deci"是 $\frac{1}{10}$ 的意思，"bel"则是以第一台电话的发明者——亚历山大·贝尔的名字命名的，最开始是在电话机行业中描述噪声对人耳的影响，因为人耳对声音的感知范围很广，以常规的十进制计数十分的不方便，所以发明了以对数表示的方法，即现在的 dB）
贝尔值 $lg\frac {S_1}{S_0}$ ，其中 $S_0$ 为基准声音强度， $S_1$ 为和基准声音对比的响度
而分贝与贝尔值的关系则是
$1dB=10B=10lg\frac{S_1}{S_0}$
这里要注意，此的公式没有写反，因为这是个相对值，原来的强度之比被分为10份，选分贝为单位时，能度量出来的声强级数值更大，所以分贝这个单位更小。或者可以这么理解， $1 B$ 表示 $S_1=10S_0$ ，而 $1 d B$ 表示 $S_1=1.2589254*S_0$ 。
1.表示功率量之比的一种单位，等于功率强度之比的常用对数的10倍。 $L=10lg\frac {P}{P_0}$
2.表示场量(如电压、电流)之比的一种单位，等于场强幅值之比的常用对数的20倍。 $L=20lg\frac {V}{V_0}$ 或 $K=20lg\frac {I}{I_0}$
说回为什么常见3dB这个量值。
$-3dB=10lg\frac {x_1}{x_0} , 3dB=10lg\frac {x_2}{x_0}$
则 $x_1=0.5011872*x_0, x_2=1.9952623*x_0$
可以发现，-3dB和3dB恰好代表了 $\frac12$ 倍和2倍
同理，10dB或者20dB（看是功率之比还是电压电流之比）代表了 $x_1$ 为 $x_0$ 的 $\frac1{10}$ 倍或10倍

混叠

限带信号 $f (t)$ 是指其频谱宽度有限的信号，即频谱函数 $\omega)$ 满足“ 当 $\mid \omega \mid> \omega_{m}$ 时有 $\omega)=0$ ”
频域卷积定理（频域上的卷积（的 $\frac{1}{2 \pi}$ 倍） = 时域上的相乘）
若 $f_{1}(t) \leftrightarrow F_{1}(j \omega)$ $f_{2}(t) \leftrightarrow F_{2}(j \omega)$
则有 $f_{1}(t) f_{2}(t) \leftrightarrow \frac{1}{2 \pi} F_{1}(j \omega)F_{2}(j \omega)$ 或 $f_{1}(t) f_{2}(t) \leftrightarrow F_{1}(j {2 \pi} \omega)F_{2}(j {2 \pi} \omega)$
其中 F代表傅里叶变换
抽样序列 $s (t)$ ，信号 $f (t)$ ，取样信号 $f_{s}(t)$ ，三者之间的关系为 $f_{s}(t) = f(t)s(t)$
冲激函数卷积的性质 $f(t)*\delta(t-\tau) = f(t-\tau)$
综上，当 $s (t)$ 为均匀冲激函数序列 $\delta_{T_{s}}(t)$ 时，即
$\delta_{T_{s}}(t) = \sum_{n=-\infty} ^{\infty} \delta(t-nT_{s})$
则其频谱函数(单位冲激序列的傅里叶变换)：
$\omega_{s}\sum_{n=-\infty} ^{\infty} \delta(\omega-n\omega _{s})$
则抽样信号 $f_{s}(t)=f(t)s(t)$ 的频谱函数为
$\begin{equation*} %加*表示不对公式编号 \begin{split} F_{s}(j \omega) & =\frac{1}{2 \pi}F(j \omega)*S(j \omega) \\ &= \frac{1}{2 \pi}F(j \omega)*\omega_{s}\sum_{n=-\infty} ^{\infty} \delta(\omega-n\omega _{s}) \\ & = \frac{\omega_{s}}{2 \pi}\sum_{n=-\infty} ^{\infty} F(j \omega)*\delta(\omega-n\omega _{s}) \\ & = \frac{\omega_{s}}{2 \pi}\sum_{n=-\infty} ^{\infty} F[j(\omega - n \omega_{s})]\\ & = \frac{1}{T_s} \sum_{n=-\infty} ^{\infty} F[j(\omega-n \omega_s)] \end{split} \end{equation*}$
也就是经典的下面这张图，其中 $w_m$ 是限带信号 $f (t)$ 的频谱宽度（或者说最大频率）， $w_s$ 是采样频率。只有当 $w_s \geq 2w_m$ 时才不会发生混叠

时域抽样定理
一个最高频率为 $f_{m}$ （角频率为 $w_{m}$ ）的限带信号 $f (t)$ 可以用均匀等间隔 $T_{s}\leq \frac{1}{2f_{m}}$ 的抽样信号 $f_{s}(t) = f_{s}(nT)$ 值唯一确定。这就是时域抽样定理。
连续信号离散化时的最大允许抽样间隔 $T_{s}=\frac{1}{2f_{m}}$ ，此间隔称为奈奎斯特(Nyquist)间隔。对应的抽样频率 $f_{s}(t) = 2f_{m}$ 称为奈奎斯特频率(或 $\omega_{s}=2\omega_{m}$ )，即最低允许的抽样频率

2. 信号与系统频域分析的工具

Fourier变换与Fourier级数

若 $f (t)$ 在 $(-\infty, +\infty)$ 上满足下列条件（Fourier积分定理）：

$f (t)$ 在任一有限区间上满足Dirichlet条件（即函数在该区间满足：1. 连续或只有有限个第一类间断点；2. 只有有限个极点值）；
$f (t)$ 在无限区间 $(-\infty, +\infty)$ 上绝对可积。
那么在 $[-\frac{\pi}{2},\frac{\pi}{2}]$ 上就可以展开成Fourier级数。在 $f_{T}(t)$ 的连续点处，级数的三角形式为
$f_{T}(t)= \frac{a_0}2 + \sum_{n=1}^{\infty}(a_{0}\cos n\omega t+b_{n}\sin n\omega t)$
其中，
$\begin{equation*} %加*表示不对公式编号 \begin{split} & \omega = \frac{2\pi}T \\ & a_{0}=\frac{2}{T} \int ^{\frac{T}{2}} _{-\frac{T}{2}} f_{T}(t) \, dt \\ &a_{n}=\frac{2}{T} \int ^{\frac{T}{2}} _{-\frac{T}{2}} f_{T}(t)\cos n\omega t \, dt (n=1, 2, 3, \dots) \\ & b_{n}=\frac{2}{T} \int ^{\frac{T}{2}} _{-\frac{T}{2}} f_{T}(t)\sin n\omega t \, dt (n=1, 2, 3, \dots) \\ \end{split} \end{equation*}$
利用欧拉(Euler)公式，将Fourier级数的三角形式转换为复指数形式
$f_{T}(t)= \frac{1}{T} \sum_{-\infty}^{+\infty} [\int ^{\frac{T}{2}} _{-\frac{T}{2}}f_{T}(\tau)e^{-j \omega_{n} \tau}d \tau]e^{j \omega _{n} t}$
而对于非周期函数，可以认为 $T\to +\infty$ ，如果满足Fourier积分定理，即
$f (t)$ 在任一有限区间上满足Dirichlet条件；
$f (t)$ 在无限区间 $(-\infty, +\infty)$ 上绝对可积。
则有Fourier积分公式：
$\frac{1}{2\pi} \int _{-\infty} ^{+\infty} [\int _{-\infty} ^{+\infty} f(\tau) e^{-j \omega \tau} d \tau] e^{-j \omega t} d\omega$
三角形式的Fourier积分公式：
$\frac{1}{\pi} \int _{0} ^{+\infty} [\int _{-\infty} ^{+\infty} f(\tau) \cos \omega(t- \tau) d \tau] d\omega$
若函数 $f (t)$ 在 $(-\infty, +\infty)$ 上满足Fourier积分定理，则 $f (t)$ 的Fourier变换：
$=\mathscr{F}[f(t)] = \int _{-\infty} ^{+\infty} f(t) e^{-j\omega t}dt$
Fourier逆变换
$=\mathscr{F^{-1}}[f(t)]= \frac{1}{2\pi} \int _{-\infty} ^{+\infty} F(\omega) e^{j\omega t} dt$

多说一点，Fourier级数展开后还是频域，Fourier变换后才是频域

Laplace变换

Fourier变换的局限性：1、要求 $f (t)$ 在 $(-\infty, +\infty)$ 内满足绝对可积；2、实际工程上许多信号在时间 $t < 0$ 时都是无意义的或不需要考虑的。
所以用阶跃函数 $u (t)$ 和指数衰减函数 $e^{- \beta t} (\beta>0)$ 来乘 $f (t)$ ，再取Fourier变换，就得到了Laplace变换
$\mathscr{L}[f(t)]=F(s)=\int _{0} ^{+\infty} f(t)e^{-st}dx$
Laplace变换存在定理：

在 $\geq 0$ 的任一有限区间上连续或分段连续；
当 $t\to +\infty$ 时， $f (t)$ 的增长速度不超过某一指数函数，即存在 $M > 0$ 及 $c\geq 0$ 使得 $\mid f(t) \mid \leq Me^{ct}$

离散傅里叶变换(DFT)

$X(k)=\sum_{n=0}^{N-1}x(n)e^{-j2\pi kn/N}$
其中， $x (n)$ 为长度为L的有限长序列， $N$ 为 $0\leq \omega \leq 2\pi$ 内等间距样本的个数，且 $N\geq L$
离散傅里叶逆变换（IDFT）: $x(n)=\frac{1}{N} \sum^{N-1}_{k=0} X(k) e^{j2\pi kn/N}$

快速傅里叶变换(FFT)

FFT是DFT的一种快速算法，而不是一种新的变换，它可以在数量级的意义上提高运算速度。

z变换

序列 $x (n)$ 的 $z$ 变换及 $z$ 反变换定义为
$z$ 变换
$\mathscr{L} [x(n)] = \sum_{n=-\infty}^{\infty}x(n)z^{-n}, z \in Convergence \ Domain$
$z$ 反变换
$\mathscr{L}^{-1}[X(z)] = \frac1{2\pi j}\oint _c X(z) z^{n-1} dz$
注：Z变换则是离散时间傅里叶变换的推广，Laplace（拉普拉斯）变换对应的是连续时间傅里叶变换的推广。
在这里插入图片描述

模拟滤波器

滤波器的分类

1. 根据频率特性划分

低通滤波器(Low Pass)
高通滤波器(High Pass)
带通滤波器(Band Pass)
带阻滤波器(Band Stop)
为了避免为每一种滤波器都建立各自独立的一种理论，高通、带通、带阻滤波器都是对经过定标(得到任何截止频率)的低通滤波器进行频率变换得到的。特殊的，全通滤波器(AP)有独特的规格确定方法而占一个特殊的位置。

2. 根据脉冲响应长度（网络结构）划分

FIR

FIR(Finite Impulse Response)网络，即有限长单位脉冲响应网络。FIR网络中不存在输出对输入的反馈支路，用差分方程描述如下：
$y(n)=\sum_{i=0}^{M}b_{i}x(n-i)$
其单位脉冲响应 $h (n)$ 是有限长的:
$h(n)=\begin{cases} b_{n}, & 0\leq n\leq M \\ 0, & others\\ \end{cases}$
FIR 的设计方法有很多种，等波纹最佳逼近法、最小二乘法、窗函数法…这里不做细致讨论

IIR

IIR(Infinite Impulse Response)网络，即无限长单位脉冲响应网络。N阶IIR滤波器的差分方程为：
$y(n)=\sum_{i=0}^{M}b_{i}x(n-i)+\sum_{i=0}^{N}a_{i}y(n-i)$
对应的系统函数为：
$\frac{\sum_{i=0}^{M}b_{i}z^{-i}}{1-\sum_{i=1}^{N}a^i z^{-i}}$
IIR，根据特性来说，巴特沃斯滤波器、切比雪夫Ⅰ型/Ⅱ型滤波器、考尔（椭圆）滤波器都属于IIR滤波器；其余的设计方法还有最平坦法、最小P-范数法、约束最小P-范数法。设计方法在这里不做细致讨论。

3. 根据逼近法划分

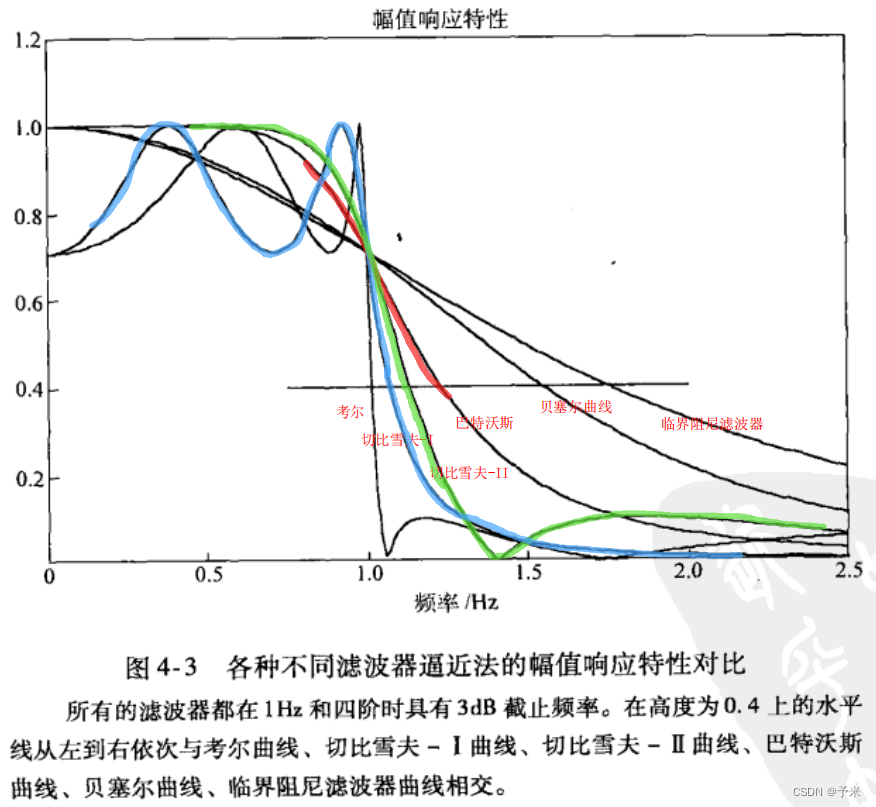
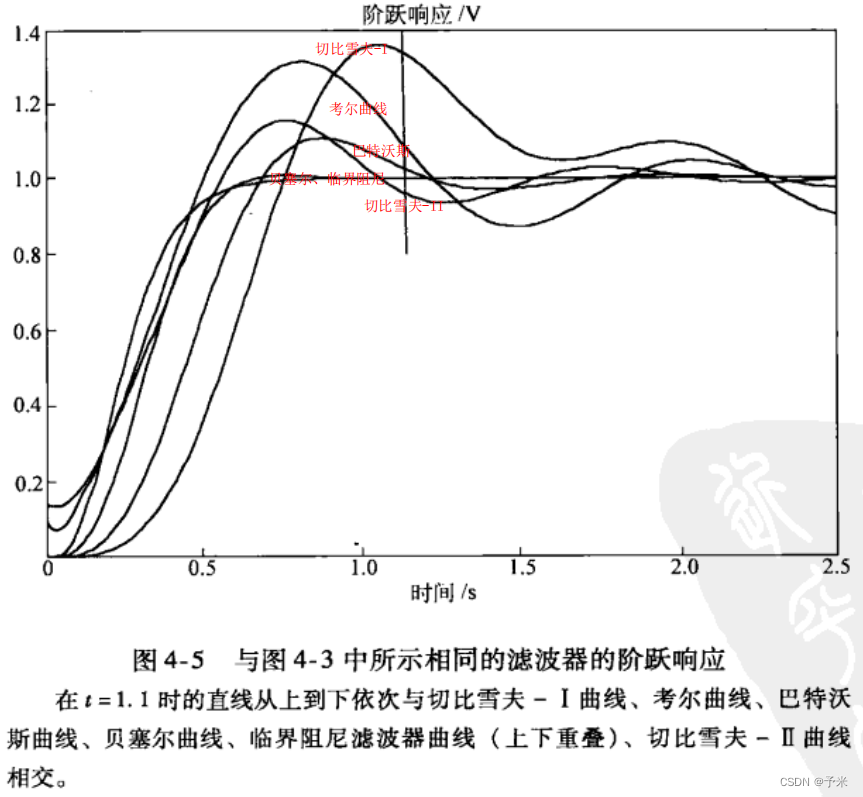
2.1 巴特沃斯(Butterworth)滤波器

N阶巴特沃斯低通滤波器的频率响应广义形式是：
$\omega) = \frac{1}{\sqrt{1+ \left( \frac{\omega}{\omega_{c}} \right)^{2n}}} = \frac{1}{\sqrt{1+\varepsilon^2 \left( \frac{\omega}{\omega_{p}} \right)^{2n}}}$
其中， $n$ 代表滤波器阶数， $\omega$ 代表电路的工作频率（通带频率）， $\omega_{c}$ 代表截止频率， $\omega_{p}$ 代表通频带边缘频率， $\varepsilon$ 代表…
在巴特沃斯滤波器中无论阶次n是几，当 $\omega$ = $\omega_{c}$ 时， $\sqrt{2}$ ，这与-3dB对应。当 $\omega\gg 1$ 时，幅值响应特性的渐近线以每十倍频 $n \cdot 20 d B$ 下降。

2.2 切比雪夫（Chebyshev）Ⅰ型滤波器

N阶切比雪夫低通滤波器的频率响应广义形式是：
$\omega) = \frac{1}{ \sqrt{1+\varepsilon^2 C_{N}^2\left( \frac{\omega}{\omega_{c}} \right)} }$
其中， $0<\varepsilon<1$ 表示通带内幅度波动的程度， $\varepsilon$ 越大，波动幅值也越大。 $\omega_{c}$ 代表通带截止频率。 $C_{N}$ 为切比雪夫多项式。

2.3 贝塞尔逼近

贝塞尔逼近法的目的是为了得到尽可能线性的相位响应特性，也就是一个恒定的群延时。
$H(s) = Ke^{-sT}$

2.4 切比雪夫Ⅱ型逼近和考尔逼近

考尔滤波器使用雅克比椭圆函数对其进行表示，故考尔滤波器也叫做椭圆滤波器

2.5 临界阻尼滤波器

需要注意的是，切比雪夫Ⅱ型滤波器和椭圆滤波器不是多项式滤波器（有零点）；巴特沃斯、切比雪夫Ⅰ型、临界阻尼滤波器都是多项式滤波器

参考文献

[1] 张元林. 工程数学积分变换(第五版)[M]. 高等教育出版社, 2012.
[2] Alan V. Oppenheim, Alan S. Willsky, S. Hamid Nawab. 信号与系统(第二版)[M]. 刘树棠译. 电子工业出版社, 2020.
[3] 吴大正, 杨林耀, 张永瑞等. 信号与线性系统分析第5版[M]. 高等教育出版社, 2019.
[4] 段哲民. 信号与系统(第三版)[M]. 电子工业出版社, 2012.
[5] 郑君里, 应启珩, 杨为理. 信号与系统(第三版)[M]. 高等教育出版社, 2011.
[6] 高西泉, 丁玉美. 数字信号处理(第四版)[M]. 西安电子科技大学出版社, 2016.
[7] 程佩青. 数字信号处理教程(第五版)[M]. 清华大学出版社, 2017.
[8]John G. Proakis, Dimitris G. Manolakis. 数字信号处理——原理、算法与应用(第四版)[M]. 方艳梅, 刘永清等译. 电子工业出版社, 2014.
[9] Martin Meyer. 信号处理——模拟与数字信号、系统及滤波器原书第3版[M]. 马晓军, 肖晖, 熊其求译. 机械工业出版社, 2011.

予米

关注

10
点赞
踩
14

收藏

觉得还不错? 一键收藏
2
评论
滤波器相关知识

如果在n0之前没有激励，那么初始条件yn0−10。在这种情况下，我们说该系统是起始弛豫的。— 如果一个系统在任意时刻n的输出[即yn]仅依赖于当前和过去的输入[即xnxn−1xn−2...]，而与将来的输入[即xn1xn2...]无关，那么这个系统就称为是因果的。ynFxnxn−1xn−2...区别在于，是否和将来的输入有关。— 如果y(n)依赖于先前的输出值[即yn−1yn−2...
复制链接

扫一扫