一. 何为相关滤波?
Correlation Filter 最早应用于信号处理,用来描述两个信号之间的相关性,或者说相似性(有点像早期的概率密度),先来看定义:
对于两个数据 f 和 g,则两个信号的相关性(correlation)为:
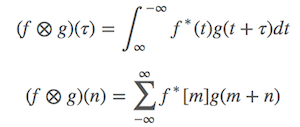
其中 f∗ 表示 f 的 复共轭,这是和卷积的区别(相关性 与 卷积 类似,区别就在于里面的共轭)。
PS:复共轭是指 实部不变,虚部取反 (a + b i)* = a - b i; 共轭矩阵是指 矩阵转置后再对每个元素求共轭,不理解的童鞋请查阅百科。
二. CF 在图像的引入 - MOSSE
可以参考经典论文 MOSSE (Minimum Output Sum of Squared Error filter)
论文下载:visual object tracking using adaptive correlation filters
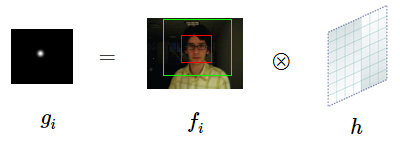
对于图像来讲,问题描述为要找到一个 滤波模版 h,与输入图像 f 求相关性,得到相关图 g。
为了方便理解,用一幅图来进行说明(相关图 g 描述目标响应,越接近时值越大):
为了加快计算速度,这里引入了傅里叶变换,根据卷积定理(correlation版本)可知,函数互相关的傅里叶变换等于函数傅里叶变换的乘积:
通过上面的公式,将复杂的互相关计算转换成 点乘。注意后面的 F(h) 是共轭,与卷积不同,公式可以简化描述为:
H* 就是我们要求的滤波器,MOSSE 提出的方法就是 最小化平方和误差,也就是针对m个样本 求最小二乘,描述为:








 本文介绍了相关滤波在目标跟踪中的应用,从基础的MOSSE算法开始,探讨了KCF的高速追踪原理,接着详细讲解了DSST如何应对尺度变化,包括Translation Filter和Scale Filter的实现细节。最后提到了相关滤波在视觉追踪领域的进一步发展,如C-COT和ECO等。
本文介绍了相关滤波在目标跟踪中的应用,从基础的MOSSE算法开始,探讨了KCF的高速追踪原理,接着详细讲解了DSST如何应对尺度变化,包括Translation Filter和Scale Filter的实现细节。最后提到了相关滤波在视觉追踪领域的进一步发展,如C-COT和ECO等。
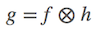
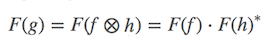

 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








