倒立摆建模

前言

本文利用现代控制理论方法，建立倒立摆系统模型，对系统进行分析，并且使用PID控制和状态反馈控制，使系统成为稳定系统。

系统模型建立

倒立摆是机器人学中一个非常重要的模型， 如图所示的倒立摆系统。 现在要研究外力 F 如何能使摆保持垂直的位置。

倒立摆相关参数符号和说明：

变量	说明
F	输入外力（N）
M	小车质量（kg）
Θ	摆杆旋转角度（rad）
m	小球质量（kg）
x	小车水平移动距离（m）
l	摆杆长度（忽略摆杆质量）（m）

对小车进行受力分析：

FN 为地面对小车的力， Flx 为杆对小车的横向力， F 为外力， Fly 为杆对小车竖
直方向的力， Mg 为小车重力。则有：

对摆进行受力分析：

Flx 为小车对杆的横向力， Fly 为小车对杆竖直方向的力， mg 为小车重力。 根据力和力矩方程， 有：

联立上述公式：

在平衡点 Θ = 0 附近线性化，有： 𝜃 = 𝑠𝑖𝑛𝜃， 𝑐𝑜𝑠𝜃 = 1， 𝜃̇’ = 0
系统方程：

定义状态变量：

得到系统状态空间方程：

为方便起见，取: 𝑀 = 1 𝑘𝑔; 𝑚 = 0.1 𝑘𝑔; 𝑔 = 9.8 𝑚/𝑠2; 𝑙 = 1 𝑚;

系统模拟结构图如下：

系统能控能观性和稳定性分析

系统能控性矩阵：

系统完全能控。

系统能观性矩阵：

系统完全能观。

系统矩阵 A 的特征方程：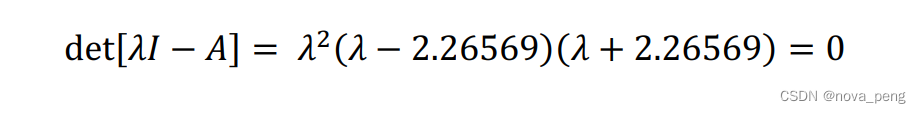
可得特征值：
由特征值可见， 系统是不稳定的。

使用 PID 控制器控制系统

使用 PID 控制器控制𝜃。
由输入 F 到输出𝜃的传递函数：

系统不稳定。

使用 PID 控制器后系统模拟结构图：
取 PID 的传递函数：

则系统传递函数：

系统极零点图：

可以看到系统所有极点都具有负实部，系统稳定。
在初始角度为 5° 的情况下，系统能控制角度到零度。

改变输入，发现输出能对输入进行跟踪，即达到了通过 PID 控制器控制角度的目的。

使用状态反馈控制

系统矩阵 A 的特征方程：

为使系统具有良好的性能， 取目标极点为：

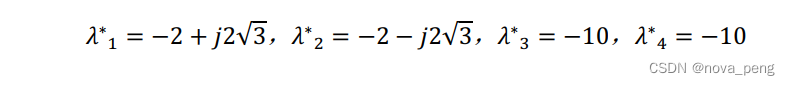
期望特征多项式：

系统转换为能控标准Ⅰ 型的变换矩阵 Tc：

能控标准Ⅰ 型状态反馈转移增益矩阵𝐾̅：

对应于系统矩阵 A，状态 x 的状态反馈转移增益矩阵 K：

加入状态反馈后系统状态空间方程：

系统矩阵的特征方程：

可得特征值：

与预期一致，系统稳定。
加入状态反馈后系统模拟结构图：

在初始角度 5° 的情况下， 偏离角度在很短时间内收敛到 0。

通过极点配置，使得系统稳定，能回到平衡点。

总结

通过对倒立摆系统建立数学模型，然后分别使用 PID 控制器控制和状态反馈控制， 实现了通过控制外力 F，进而控制摆杆角度θ的目的。
　　在 PID 控制中，虽然找到了 PID 的传递函数，使得系统稳定，并且可以控制角度θ ，但寻找合适的 PID 参数的过程过于繁琐，需要花费大量时间。同时因为 PID 单输入单输出的特性， 控制过程中只用了θ ， 也只控制θ ，没有利用其它状态变量，造成数据浪费。 能否对单 PID 控制器控制方法进行改进，根据状态变量间的导数关系，采用串级 PID，实现对系统更加简便、精准的控制。
　　在状态反馈控制中，通过计算状态反馈转移增益矩阵 K，实现了极点配置，系统能回到平衡点。 极点配置的过程相对容易，没有 PID 那样繁琐。 状态反馈时使用了四个状态变量， 在实际的应用中， 通常不会使用这么多传感器， 因此， 可以设计降维观测器，通过观测器观测出一部分状态变量，从而减少传感器的使用。 虽然系统能够稳定在原点， 但要系统能够按照我们的指令到达任意位置， 仅仅使用状态反馈是不行的， 尝试对系统进行状态反馈解耦，实现对系统的任意位置控制。