Nutcracker optimizer

Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems

摘要
受克拉克星鸦的启发，文章提出了一种自然启发的的元启发式算法：星鸦优化算法。星鸦在不同时期表现出两种不同的行为。第一种行为发生在夏季和秋季，星鸦寻找种子，随后将其存储在适当位置。另一种是基于空间记忆策略的行为，发生在冬季和春季，利用各种物体或标记物为参考点搜索不同的角度标记的贮藏物。如果星鸦找不到储藏的种子，他们会随机探索搜索空间寻找食物。这里提出NOA来模拟这些不同的行为，NOA是一种新的、鲁棒的元启发式算法，使用不同的局部和全局搜索算子，使其能够以更好的结果解决各种优化问题。通过23个标准测试功能、CEC-2014、CEC-2017和CEC-2020测试套件以及5个实际工程设计问题对NOA进行评估。NOA与现有的三类优化算法进行了比较:(1)最近发表的SMA、GBO、EO、RUN、AVOA、RFO和GTO算法，(2)SSA、WOA和GWO算法是高引用算法，(3)AL-SHADE、L-SHADE、LSHADE-cnEpSin和LSHADE-SPACMA算法是高性能优化器和CEC竞赛的获胜者。NOA方法在所有方法中排名第一，并表现出优于LSHADE-cnEpSin和LSHADE-SPACMA的最佳优化方法，是CEC-2017的获奖者，AL-SHADE和L-SHADE是CEC-2014的获奖者。

---

前言

在过去的二十几年来，由于元启发式算法的高精度、高优化速度和低计算复杂度，引起了进化算法界的极大兴趣。MH方法已被证明具有解决各种应用领域复杂优化问题的能力。Chamaani等人[31]介绍了这些方法在天线时频域优化中的应用。彭辉等[32]讨论了MH方法在土壤温度预测混合人工智能模型开发中的应用。Gao等人[33]建议将这些方法应用于动态路由问题。这些算法在医疗应用中的顺序数据处理中也显示出效率，这对于各种基因建模活动具有很高的价值[34]。此外，如[35]所述，蛋白质结构建模和分配可以通过使用MH方法的特定衍生物来解决。医疗结果的分析也可以依赖于MH方法。在医学诊断领域，定制版的MH方法在分析医学数据进行分类[36,37]和放疗计划[38]方面表现出优异的效果。最近有报道称，MH方法支持实时应用中的文本挖掘[39]和谱聚类[21]。这些蛋白质编码中的方法已被报道用于医学应用[40]。在物理应用中，许多MH方法用于提取不同光伏模型的参数[41-45]。MH方法也用于各种工程目的。Mirghasemi等[46]使用这些方法来降低图像噪声。Zhang等人[47]提出了用于机器人定位的粒子滤波。Das等人[48]对这些方法进行了详细的研究，包括最近的进展、一系列可能的应用和理论基础。MH方法由于其高精度和易于实施，预计将在生活的不同领域得到广泛应用。

大自然是大多数MH方法的灵感来源。我们可以看到动物捕猎、繁殖或旅行寻找食物的奇妙方式。我们也可以在植物界看到令人兴奋的现象和激发科学发展的自然元素。这些行为最近在各种优化技术中进行了建模，其结果总结在表1中。

在最先进的MH算法中，我们有许多著名的经典模型，例如在[49]中提出的模拟退火模型，其中使用燃烧铁和其他金属的概念构建了最早的优化技术之一。在文献[50]中提出的遗传算法(genetic algorithm, GA)是目前最流行的模拟基因进化的优化算法之一。GA包含不同类型的随机性。该算法随机进行选择、复制、变异等操作，极大地避免了局部最优。**随机行为是优化算法的主要特征，它导致了不确定性的结果。**人类模仿自然的想法是成功的，因为个体动物之间相互作用和生命交流的模式的发展被选为改进的策略。粒子群优化算法[1]是这些算法中最早也是最流行的一种。[51]中提出的可微进化是受到自然进化现象概念的启发。[2]中提出的蚁群优化是受到蚂蚁觅食行为的启发。[6]中提出的人工蜂群模拟了蜜蜂觅食和产蜜的行为。[7]中提出的杜鹃搜索算法模拟了杜鹃繁殖寄生的行为。文献[9]模拟了蝙蝠的回声定位能力，在蝙蝠算法(Bat Algorithm, BA)中提出了基于回声定位的自定义运动模型。文献[10]从花的授粉过程中得到启发，提出了一种花的授粉算法。文献[15]提出了一种蚁狮优化器，它模拟了蚁狮伏击在解空间中寻找最优点的方式。[18]中提出的salp swarm algorithm (SSA)模拟了salp在海洋中导航和觅食时的群体行为。近年来提出了许多基于动物生活的某些特征的优化算法，如独特的狩猎方式、寻找食物或繁殖的迁徙方式以及其他生活方式。[23]中提出的海鸥优化算法模拟了海鸥在自然界中的迁徙行为。参考文献[24]提出的黏菌算法，模拟了自然界中黏菌的振荡方式。Ref.[26]提出了一种红狐优化算法，该算法模拟了红狐在狩猎过程中的奇怪形状，因为它使用不同的策略来分散猎物的注意力，接近猎物，然后扑向猎物。[29]中提出的食肉植物算法是最近引入的优化算法之一，该算法模拟了食肉动物如何在恶劣环境中狩猎生存。最新的算法受到蜂鸟的启发，模仿蜂鸟的飞行技能和觅食的智能策略[30]。在[52]中改进了黑猩猩优化算法(chimp optimization algorithm, ChOA)，以帮助搜索代理从探索模式过渡到利用模式。此外，在[53]中，将小生境技术与ChOA相结合，通过在优化过程中保留黑猩猩的多样性来防止过早收敛。参考文献[54]提出了灰狼优化器的一种新变体，称为跨维协调灰狼优化器(CDCGWO)，它采用了一种新的学习技术来保持灰狼的多样性，以避免在多模态优化任务中过早收敛。

MH方法称为随机方法。正如这些技术的名称所示，它们最初随机执行优化。优化过程从创建一组随机解开始。通过预先确定的步骤，通过迭代或生成，将这些初始解决方案组合、转换或开发。这些方法彼此不同，因为它们在改进过程中使用不同的方法来组合、转移或开发解决方案。

MH方法已成为解决各种优化问题的确定性方法的有力替代方案。尽管确定性方法在解决涉及线性(单峰)搜索空间的问题时是有效的，但当它们应用于非线性搜索空间问题时，包括非凸现实世界问题，它们往往会陷入局部最优状态[55]。此外，确定性算法需要梯度信息，并且机械地、迭代地工作，没有任何随机性。相比之下，MH方法不需要梯度信息，并且在随机性质下工作，这使得它们可以在搜索空间中搜索所有最优解，同时避免局部最优。MH优化方法有两个关键特征：exploration （探索）和 exploitation（开发）。探索即全局搜索能力，与逃避局部最优和防止相同的停滞有关。同时，开发是在当地开发有潜力的地区以提高其质量的能力。这两种属性之间的良好折衷会产生最佳性能。所有基于种群的算法都使用这些属性，但使用不同的操作符和过程。

尽管传统算法和现代算法都取得了成功，但没有一种算法能保证找到所有优化问题的全局最优解。“天下没有免费的午餐”[56]理论从逻辑上证明了这一观点。因此，研究人员被激励去设计新的和更有效的算法。在本文中，我们提出了一种新的优化算法，灵感来星鸦在寻找优质食物的行为及其在食物储存中的行为。这项工作还展示了鸟类再次寻找储存的食物并取回食物的独特行为。上述星鸦的奇异和独特的行为促使研究人员设计了一种新的优化算法模型，该模型被证明可以有效地解决各种优化问题。

---

2、自然界中的克拉克星鸦

Clark 's nutcracker, Nucifraga columbiana，是一种高纬度居住的鸦科物种(鸦科)，生活在美国西部和加拿大的山区[57,58]。像其他鸦科物种一样，克拉克的星鸦以其非凡的智慧而闻名。克拉克的星鸦是一种浅灰色的鸟，有着黑色的翅膀(见图1)。这些鸟经常独自生活，不像乌鸦等鸦科的其他物种那样生活在家庭群体中。这些鸟的受欢迎程度源于它们与松树的正向关系。松子是克拉克星鸦的主要食物来源。同时，克拉克星鸦是白皮松(Pinus albicaulis)的主要种子传播者[59,60]。几项研究表明，白松数量的下降对星鸦的数量产生了负面影响[61-64]。

克拉克星鸦被认为是最专业的分散囤积鸟类之一，是白皮松种子的有效传播者。星鸦运输和存储松子的方法是独一无二的。秋天种子大丰收的时候，一只星鸦可以储存大约22000到33000颗松子，储藏到数千个位置。星鸦依赖储藏的种子过冬，即使在厚厚的积雪下也能找到种子。储藏一直持续到种子作物枯竭或恶劣天气来临。此外，星鸦可以高效率得从树上搜集种子，也可以识别可食用的种子和不能食用的种子。他们能够选择出饱满种子数量高于平均水平的松果，并专注于选择那些生产好松果的树木。星鸦有一个舌下袋，每次可以携带多达90颗松子[67-69]。种子可以从收集区(松树)运输32公里到临时储存地点，在那里它们被成组地埋在地下2-3厘米深的贮藏库中(通常是4-5颗松树种子)[67,70 - 73]。这些种子被埋在没有树木的高地或朝南的山坡上，那里的雪在春季融化得最早。

星鸦选择的松子饱满是因为他们大且容易获得。此外，星鸦更喜欢当地丰富的树木，因为它们从松果密度较高的树上收集种子[76,77]。星鸦也会选择有活力的种子，这对松树有积极的影响，因为这增加了它们繁殖的机会。此外，星鸦将大量种子临时储存，减少了对水分和空间的竞争[72，78]。种子储存的深度与发芽要求相适应，所选的许多位置适合种子发芽[61，64，78，79]。

星鸦利用空间记忆来检索存储在地下的食物。实验显示，星鸦可以记住存储位置长达9个月。它们利用视觉线索来回忆每组储藏物的具体位置[83-85]。研究人员发现星鸦以两个或两个以上的物体作为线索。当星鸦挖洞时，它会看到两到三样东西附着在这个地方：一块凹凸不平的岩石、一丛灌木、一根树干等。研究表明星鸦可以记住高达80%的埋藏物。然而，由于各种原因，星鸦无法将食物放入储存库，要么仓库被另一只星鸦偷走，要么由于自然或其他因素被破坏。

本文基于星鸦搜索、缓存和恢复等行为引入一种新的自然启发的元启发式算法。在下一节中，将对这些行为进行数学建模，并提出一种星鸦优化算法(NOA)。

二、星鸦优化算法（NOA）

提出了一种基于星鸦智能行为的仿生优化算法(NOA)。如上文述，星鸦的行为可以划分为两部分：一是搜集松子并储藏；二是搜索并检索储存位置。这两种发生在两个不同的时期。第一张行为发生在夏季和秋季，而第二种行为发生在冬季和春季。在提出的算法中，我们基于上述两个主要行为来模拟星鸦的行为。两种主要策略是(i)觅食和储存策略;(ii)缓存搜索和恢复策略。这些策略可以解释如下。

3.1.觅食和存储策略

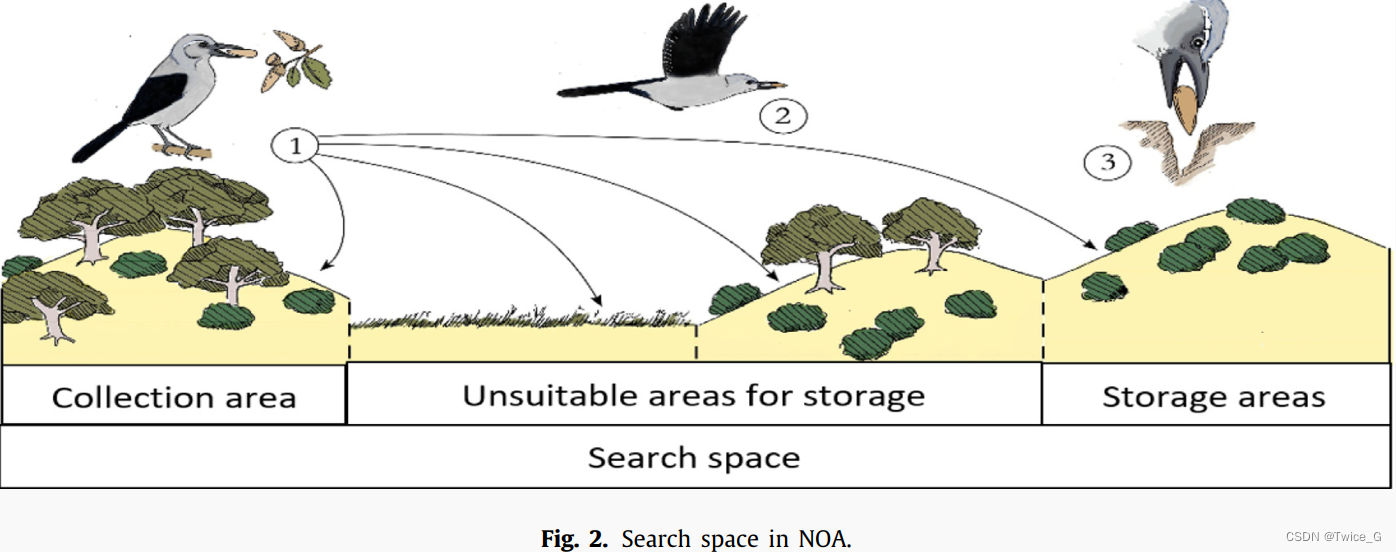
星鸦在松林中随机搜索松子。将松林称为收集区域。星鸦选择包含较好松子的松果。如果星鸦在所选择的松树上没有找到理想的松子，就会探索收集区域的其他松树。这一行为称之为第一探索阶段。然后，星鸦会开发大量松子并将它们储存在远离收集区域的地方。星鸦将收集到的松子运送到合适的储藏区域，通常是没有茂密森林的高地，如图2所示。除了其他与天气有关的原因外，地势低洼和树木繁茂的地点容易受到偷猎或啮齿动物和鸟类的破坏。这种行为称为第一个开发阶段。

3.2.缓存搜索和恢复策略

冬天，星鸦开始搜索储存的种子。这一行为称为第二探索阶段。星鸦不仅会随机寻找它们的贮藏物，还会利用贮藏物附近的物体作为线索来确定它们的位置。此外，星鸦使用空间记忆作为主要机制来帮助恢复它们的缓存。它们在一个储藏点附近使用多个对象，并且能够长时间记住储藏物的位置。星鸦利用食物储藏来养活自己和它们的孩子长达6个月。这种行为称为第二个利用阶段。星鸦更依赖空间记忆生存。然而，星鸦有时找不到贮藏物，所以它们寻找另一个贮藏点来获取食物。

实际上，上述两种行为发生在不同的阶段：星鸦在每年的晚夏和秋天搜集松子，并埋藏，作为冬季和春季的主要食物来源。上述所提到的所有星鸦的行为被数学模拟，从而提出一种新的MH方法来解决优化问题。

3.2.缓存搜索和恢复策略

本工作的总体目标是提出一种新的优化方法，模拟胡桃夹子在松树种子的觅食、储存和恢复中的行为。从这种行为衍生出的以下原则实现了本算法的基本假设:
1）星鸦以个体的形式存在。
2）星鸦在两个时期有两种行为。
3）星鸦在收集区域寻找有效的松子。
4）星鸦把收集到的松子带到远离收集区域的地方并将它们埋起来。
5）星鸦记住埋藏种子的地方。

实际上，星鸦可以有多个埋藏点。简单起见，我们假设每只星鸦仅有一个食物源，一个埋藏点。具体来说，一个解 $X_i$ 相当于一个星鸦或一个食物源。在未来的研究中，我们可以很容易地扩展到每个星鸦有多个缓存，多目标优化问题也可以扩展到多个星鸦。

NOA的框架如图3所示。NOA有一个简单的框架包含两种策略当表了发生在不同时期的两种行为。第一种策略代表星鸦搜索食物源并将其存储在合适地点的行为。第二种策略代表星鸦寻找和检索存储位置的行为。NOA中，搜索空间可以划分为两种区域：第一种是收集区域，星鸦在此区域收集食物；第二个是储藏区域，星鸦在此区域存储食物。NOA中，两种策略的信息共享机制如图3所示，每一种策略都包含局部开发和全局搜索。 总而言之，该图描述了NOA模拟星鸦行为的一种能够解决各种优化问题的新型元启发式算法。优化过程的开端，一群星鸦探索搜索空间寻找他们的食物，即松子。发现的松子储存在适当的储藏点，在冬季和 春季取回，直到星鸦繁殖并存活。在夏季和秋季，星鸦遵循的第一种机制被定义为觅食和存储策略，该策略采用探索算子作为第一阶段，探索搜索空间，寻找最有希望包含种子的区域。在这一阶段之后，开发人员将被要求将发现的松树种子储存在一个适当的储存库中，储存库上标有各种物体或标记，作为线索，帮助他们在冬季和春季找到松树种子。在冬季和春季，星鸦遵循基于空间记忆策略的不同机制来搜索和检索储存的松树种子。这一机制被称为缓存搜索和恢复策略。在该策略中，基于标记松子隐藏位置的参考点，使用探测算子对这些参考点周围的区域进行探测，以找到存储的松子。当发现隐藏的松子时，开发算子将被激发以取回埋在地下的松子。下一节将对这两种策略进行详细解释。

3.3.1.觅食和存储策略

上述机制可分为觅食和储存两个主要阶段，具体描述如下:

• Foraging stage: Exploration phase1 (觅食阶段：探索阶段1)
  在这个阶段，星鸦开始在搜索空间(收集区域)中采取由式(19)生成的初始位置/食物位置（随机初始化）。每只星鸦开始在检查初始位置上的松果所包含的种子。如果星鸦找到较好的种子，它会将其带到储藏区域并将其埋藏至隐藏点。如果星鸦不能找到好的种子，它会寻找松树上或者另一个树的松果。他的行为可以用位置更新策略数学建模如下:
  
  其中$X_i^{t+1}$ 是第$i$个星鸦$t+1$次迭代的位置；$X_{i,j}^t$是第$i$个星鸦当前代的第$j$个位置；$U_j$和$L_j$是优化问题第$j$维的上界和下界，$\gamma$是根据莱维飞行生成的随机数，$X_{best,j}^t$是目前得到的$j$维最佳解。A,B,C是三个随机数；${\tau }_1$，${\tau }_2$，$r$和$r_1$是$[0,1]$之间的随机实数；$X_{m,t}^j$是当前种群在迭代$t$中所有解的第$j$维均值;$\mu$是基于正态分布${\tau }_4$， 莱维飞行${\tau }_5$，0到1之间随机数${\tau }_3$生成的数，如下式所示:
  
  其中$r_2$和$r_3$是$[0,1]$之间的随机实数。建议采用Eq.(1)来考察优质食物来源。Eq.(1)的第一个分式模拟了星鸦在第一次尝试中发现好种子的概率。这个概率意味着星鸦不会改变
  解${\vec{X}}_i^t$中的原始第$j$维。Eq.(1)的第二个分式，允许星鸦在搜索空间中全局探索随机位置，以增强NOA的搜索能力，尽可能地探索搜索空间，避免陷入局部极小值，到达可能包含近最优解的有希望区域。Eq.(1)的第三个分式，允许星鸦探索从总体中随机选择的解周围的位置，除了在第二个分式下以$\delta$概率在搜索空间中全局移动所覆盖的区域之外。后面介绍对$\delta$最佳估计值的敏感性。A和B向星鸦提供新的食物位置信息。${\tau }_1$和${\tau }_2$
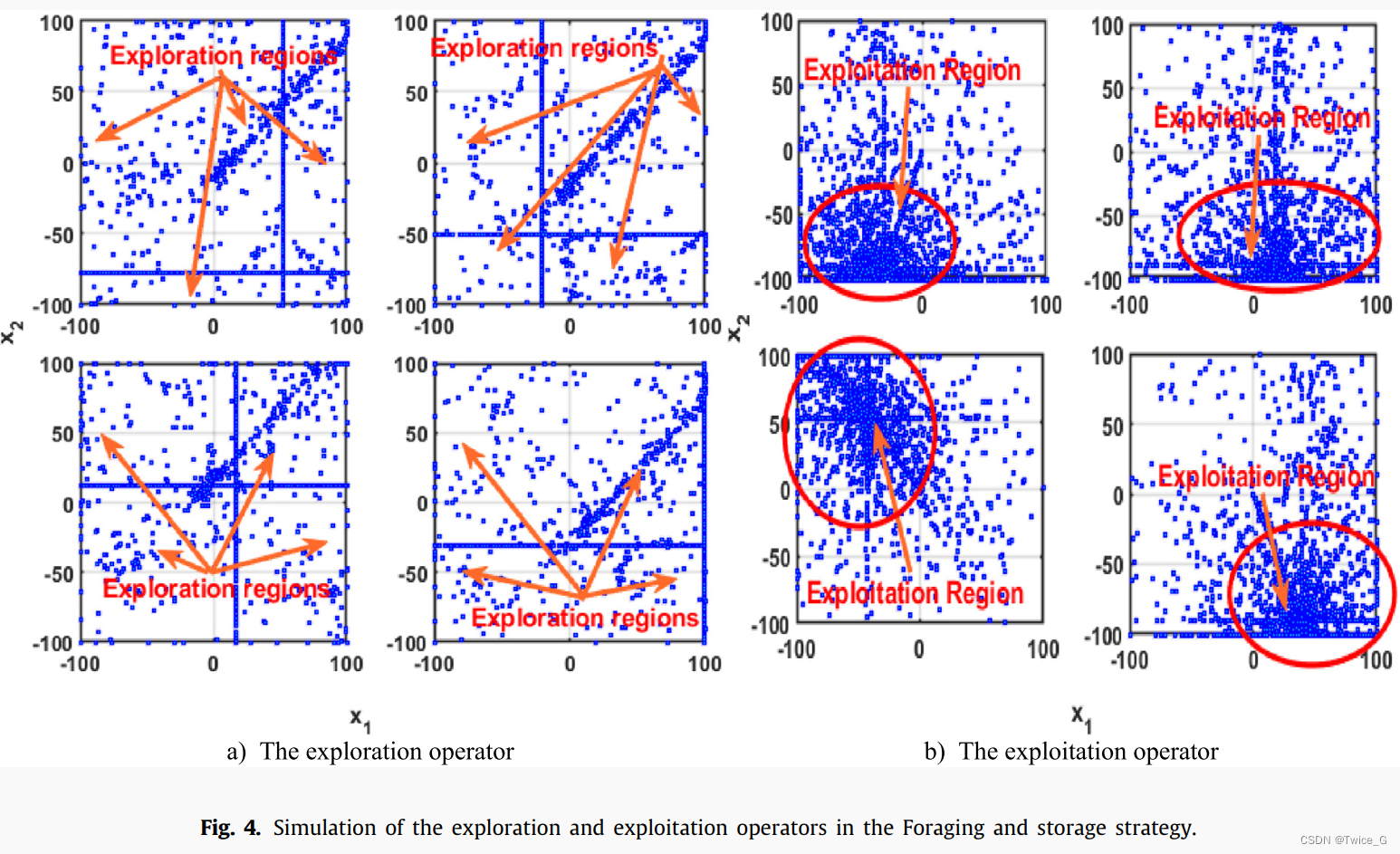
  作为尺度因子来调整NOA的勘探能力。该算法可以在${\tau }_1$和${\tau }_2$的大小范围内，交替进行局部和全局搜索。$\mu$向星鸦提供所需方向和步长信息以探索新的位置。图4(a)中描述了四次独立运行的探索阶段，以显示在搜索空间内探索区域的能力。从图中可以看出，在整个优化过程中，大部分搜索空间都被觅食阶段下生成的解所覆盖，从而肯定了这一阶段的有效性，正如后来进行的实际实验所证实的那样。
  
• Storage stage: Exploitation phase 1 (储藏阶段：开发阶段1)
  星鸦开始将上一阶段找到的食物运输到储藏点（储藏区域）。这个阶段被称为“开发阶段1”，在这个阶段，星鸦开发松树种子作物并储存它们。这种行为可以用数学形式表示如下:

其中${\vec{X}}_i^{t+1（new)}$是当前星鸦储存区域的新位置，$\lambda$是根据莱维飞行所生成的随机数，${\tau }_3$是$[0,1]$之间的随机数，$l$是一个从1到0的线性递减因子，以多样化NOA的开发算子。除了避免在一个方向搜索时可能出现的陷入局部极小值之外，NOA开发算子的这种多样性将有助于加快其收敛速度。

优化过程，觅食阶段与储藏种子之间的交换按照下式进行以保持探索和开发之间的平衡:

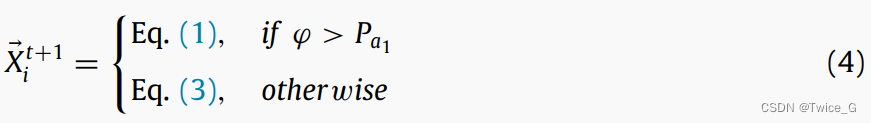
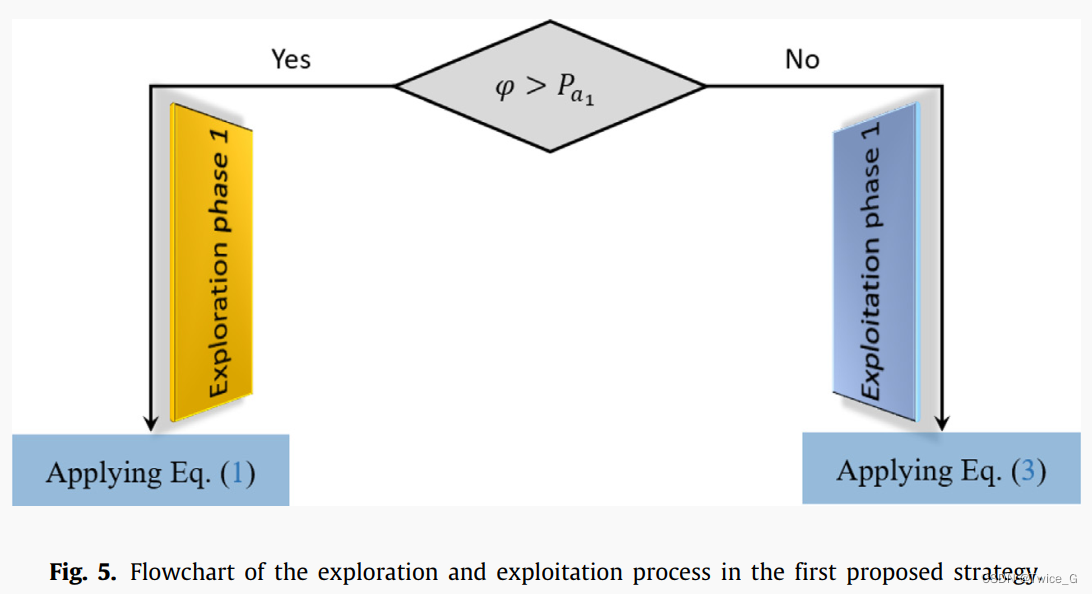
其中$\phi$是一个1到0之间的随机数，$P_{a_1}$是一个概率值，基于当前代从1线性减小到0。如图4(b)所示为该阶段生成的解的方向，这证实了该阶段可以在搜索接近最优解的同时，将大多数解引导到一个区域的方向，以尽可能多地覆盖该区域的解。在第一种提出的策略中，探索和开发过程的流程图如图5所示，并在算法1中列出。

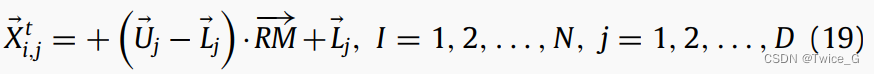
3.3.2.参考记忆

在将种子埋藏之后，星鸦激活空间记忆。星鸦根据记忆以特定的物体为线索帮助他们找到储藏的食物。星鸦几乎依靠他们记忆中储藏的食物以度过整个冬天。星鸦仔细检查并画出储存位置。隐藏的食物是他们繁衍和生存的唯一机会。此外，星鸦似乎以较大的地形特征或高大的树木作为标志，而局部特征则没有用处，因为它们在冬天被雪覆盖。接下来，我们将模拟星鸦检索储藏食物时的行为。

3.3.3.储藏搜索和找回策略

这一策略可以分为两个阶段：储藏搜索和找回阶段。具体描述如下：

• Cache-search stage: Exploration phase 2（储藏搜索阶段：探索阶段2）
  当冬天来临，树木变得稀少，开始由隐藏模式转变为探索和搜索模式。星鸦开始搜索他们的储藏，称之为第二探索阶段。星鸦利用空间记忆策略定位储藏地点。对于单一的储藏点星鸦更倾向于使用多个参考物为记号。为了简单起见，我们假设每个隐藏点仅有两个参考物。参考物将来自隐藏点的不同角度。在这一阶段，在搜索空间中（储藏区域），星鸦的初始（储藏）位置由Eq.(19)生成。在NOA中，种群的每个储藏点/星鸦的两个参考点（RPs）矩阵定义如下:
  
  其中${\overrightarrow{RP}}_{i,1}^t$和${\overrightarrow{RP}}_{i,2}^t$表示当前代$t$，第$i$个的星鸦储藏点位置${\vec{X}}_i^t$的参考点。为了说明星鸦、储藏点和参考点三者的关系，我们假设这三个元素代表了三角形的三个顶点。星鸦可以放置在不同的位置和不同的角度。图6描绘了星鸦三维空间中的三个不同位置，其中一个储藏点有三个不同的参考位置。假设储藏点位于3D空间的原点。星鸦的视角各不相同。第一个位置是锐角，第二个位置是钝角，第三个位置是直角。星鸦可以在3D空间的任何地方找到，坐标轴或者对线轴上。参考点也是一样的。
  
  星鸦可以以高精度发现储藏点。然而，根据相关研究，接近20%的星鸦第一次尝试失败。如果星鸦不能通过第一个参考点定位到储藏的食物，它会根据第二个参考点确定。如果荥阳第二次仍然没有找到，它就会利用第三个参考物。设计了两种不同的方程来生成第一和第二参考点，以改善星鸦在寻找隐藏贮藏物时的探索操作。第一个参考点通过在相关领域内更新当前位置来找到星鸦周围隐藏的贮藏物。第一个参考点的更新公式如下：
  
  第二个参考点是通过在问题的搜索空间内更新当前解来生成的，以帮助星鸦探索不同的区域来寻找隐藏的贮藏物。第二个参考点的计算公式如下：
  
  其中$k$是参考点的索引；${\overrightarrow{RP}}_{i,k}^t$是当前代$t$，第$i$个的星鸦储藏点位置${\vec{X}}_i^t$的第$k$个参考点；$\vec{U}$和$\vec{L}$是D维优化问题的上下界，$\alpha$从1到0线性递减，${\vec{r}}_2$是一个包含0到1之间随机生成值的向量；${\vec{X}}_A^t$为当前代$t$第$A$个星鸦的储藏点位置；${\tau }_3$是一个$[0,1]$之间的随机数；$\theta$是$[0，\pi ]$之间的随机数；$P_{rp}$用于确定在搜索空间内全局探索其他区域的百分比的概率。
  Eqs. (6) 和 (7) 被用于生成每只星鸦的两个参考点以复原储藏点。当参考点接近储藏点，可以很容易得将其找回。我们假设第一代星鸦没有足够的经验来选择参考点（储藏点附近），然而随着时间的推移，星鸦获得更多经验。星鸦在他们的储藏地附近回想标记物，这样以后就可以很容易地找到它们。方程中的$\alpha$用来训练星鸦，并给它们足够的经验选择适当的位置作为参考点。在NOA中，$\alpha$有避免了参考点向解（储藏点）过早收敛。$\theta$是星鸦的视角，在$[0，\pi ]$之间随机选择。星鸦的不同视角如图7所示。当$\theta =\pi /2$时，${\overrightarrow{RP}}_{i,k}^t={\vec{X}}_i^t$，意味着参考点和储藏点一致。为解决这一问题，Eqs. (6) 和 (7)修正为：
  
  
  其中${\overrightarrow{RP}}_{i,1}^t$表示Eq.(5)所示矩阵中的第$i$行和第一列，${\overrightarrow{RP}}_{i,2}^t$是矩阵中的第$i$行和第二列。矩阵的行索引表示储藏点/星鸦的索引，列索引代表参考点的索引。RP（参考点）是一个随机位置。Eq.(9)和Eq.(10)的第一个分式（即，$\theta =\pi /2$）是为了避免参考点过早收敛于可能解。$\alpha$确保NOA定期收敛，允许星鸦在下一代中改进其RP选择。$\alpha$计算方式如下：
  
  其中$t$和$T_{max}$分别代表了当前迭代次数和最大迭代次数。Eq.(11)中的第一分式随着迭代线性减小，提高了算法的收敛速度。同时，第二分式线性增加，以避免陷入局部极小值，这可能是由于第一分式造成的。
  在优化过程中，所有的星鸦在选择适合的参考点时获得足够的经验。这些星鸦根据适当的RP更新储藏点位置/解决方案。在NOA中，所有星鸦都将应用探索机制来搜索可能包含近似最优解的最有希望的区域。随着一次次迭代，算法将以适当的PRs探索和开发储藏点周围的区域，以避免陷入局部最小值。星鸦的位置更新如下：
  
  其中${\vec{X}}_i^{t+1}$是第$i$个星鸦$t+1$次迭代的新位置，${\vec{X}}_i^t$是第$i$个星鸦的当前位置，${\overrightarrow{RP}}_{i,1}^t$是第一参考点。Eq(12)来指导NOA对${\overrightarrow{RP}}_{i,1}^t$周围有潜力的区域进行探索和开发。如果星鸦不能在${\overrightarrow{RP}}_{i,1}^t$周围探索到最有希望的区域，它就会探索其他区域，例如，参考点${\overrightarrow{RP}}_{i,2}^t$附近的区域，具体讨论见下文。
  ![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/ec7da6e141004032b1c713d27616424f.png
• Recovery stage: Exploitation phase 2（找回阶段：开发阶段2）

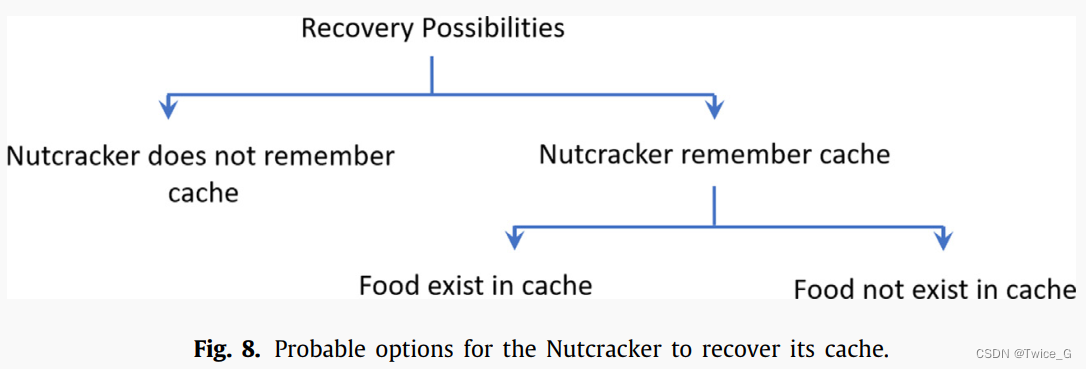
图8描述了星鸦在搜索储藏点时可能遇到的可能性。第一个主要的可能性是，星鸦可以使用第一个RP记住他储藏点的位置。图8所示的两种可能性如下：第一种是食物存在，第二种是食物不存在。这一行为的数学表达式如下：

其中${\vec{X}}_i^{t+1}$是更新后的位置，$j$是维度索引，${\vec{X}}_{best}^t$是当前迭代的最佳位置，${\overrightarrow{RP}}_{i,1}^t$是第$i$个星鸦当前位置的第一个参考点（PR），$r_1$、$r_2$、${\tau }_3$和${\tau }_4$是$[0,1]$之间的随机数，$C$是种群中随机选择的解的索引。

Eq.(13)的第一个分式模拟了第一种可能性（食物存在）。这意味着该解中的一些维度有机会存活到下一代。事实上，保存松子的仓库是很好的，所以星鸦下次会优先考虑食物储存。Eq.(13)的第二个分式模拟了第二种可能性（食物不存在）。在这种情况下，解域并不理想，因此算法采用逃逸机制，避免陷入局部极小值。储藏处的食物因为某些原因丢失：或者被其他星鸦偷了，或者被自然因素破坏，例如雨或者雪。Eq.(13)的分式(1)允许星鸦在搜索空间中开发有希望的区域，以增强NOA的局部搜索能力。Eq.(13)的分式(2)允许星鸦在搜索空间中探索随机位置，以增强NOA的全局搜索能力。

第二种主要可能性是星鸦利用第一个参考点没有找到被隐藏食物的位置，因此它会利用第二个参考点搜索。实际上，星鸦在他的记忆中保留了许多参考点（PRs），这些参考（PRs）将在早期存储期间使用。星鸦在第一次尝试找回储藏物(使用一个参考点)，但在所提出的算法中考虑了第一次尝试失败的概率。找不到贮藏地点的星鸦会利用当地的地标，这些地标可能会在秋天(储藏时间)和冬天(找回时间)之间的天气变化时消失。星鸦的空间记忆Eq.(12)使用第二个RP进行更新:

Eq.(14)为NOA提供了一个机会，可以探索第二个RP周围的新区域，并开发可能找到潜在解决方案的有前途的区域。在NOA中，假设星鸦使用第二个参考点找到它的储藏点，因此根据第二个参考点更新式(13):

其中，$r_1$、$r_2$、${\tau }_5$和${\tau }_6$是$[0,1]$之间的随机数。Eq.(15)的第一个分式允许算法围绕涉及最优解的最合适区域加强局部搜索。Eq.(15)的第二个分式允许算法在搜索空间中搜索新的区域，以增强其全局搜索能力。综上所述，对找回行为的模拟(图8)可以总结为:

其中${\tau }_7$和${\tau }_8$是$[0,1]$之间的随机数。上式第一种情况表示星鸦记住了储藏点，而第二种情况表示星鸦没有记住储藏点。现在，关于第一个参考点和第二个参考点的探索行为之间的权衡是根据以下公式实现的:

最后，储藏点搜索阶段与找回阶段的交换按照下式进行，以保持勘探与开采的平衡:

其中$\varphi$是$[0,1]$之间的随机数，$P_{a_2}$表示一个概率值，该概率值等于0.2，根据后面实验所确定的。根据图9所示的储藏点搜索和找回策略特征的仿真实验，一方面，该策略中的探索算子具有很强的覆盖能力，表示参考点跟随星鸦寻找隐藏点的大范围分布能力。另一方面，如图9(b)所示，开发算子将搜索范围缩小到一个小区域内，以找回隐藏点中的松树种子。第二种策略的探索和开发过程流程图如图10所示，并在算法2中列出。

---

4.算法实现

NOA算法包含两种策略：一是觅食和存储策略，二是储藏点搜索和找回策略。两种策略对NOA同样重要，以相同的概率被选择。与其他基于种群的优化算法相似，NOA种群初始化如下：

其中$t$为代数索引；${\overrightarrow{U}}_j$和${\overrightarrow{L}}_j$分别为D维问题的上下界；$\overrightarrow{RM}$是$[0,1]$之间的随机向量。每只星鸦代表问题的一个可行解。

第一个提出的策略称为第一探索和开发阶段。第二种策略称为第二探索和开发阶段。在这两种策略中，探索和开发阶段对NOA的重要性是相同的；因此，它们被随机交换来模拟星鸦的行为，同时根据需求采用第一或第二种策略。

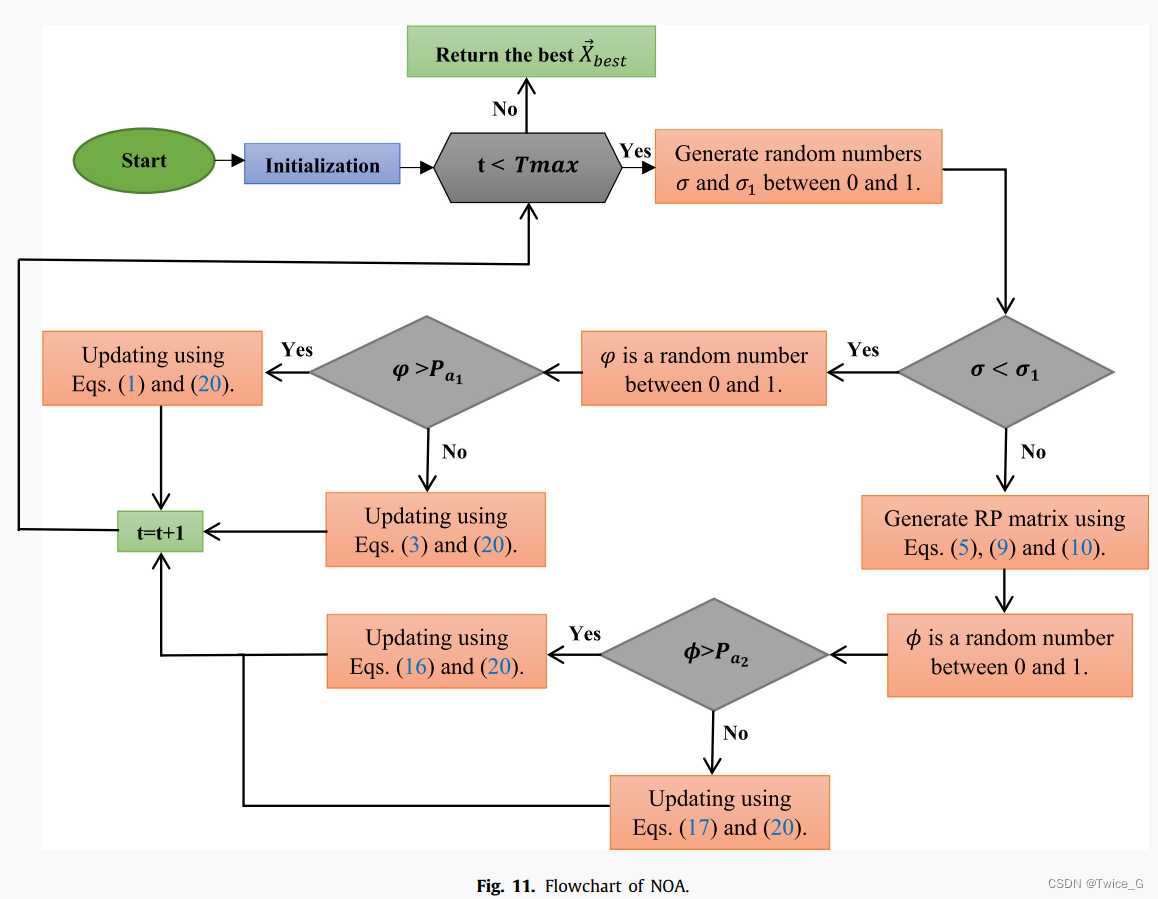
在第一个所提出的策略中，每个星鸦/源代表当前迭代中的一个潜在解决方案，每个缓存代表该迭代中的一个潜在解决方案。在第二个所提出的策略中，每个星鸦/储藏点代表当前迭代中的一个潜在解决方案，每个RP代表该迭代中的一个潜在解决方案。每只胡桃夹子都有一个食物源和一个搜索空间中的储藏点。根据适应度函数对星鸦的每个新位置的解的质量进行评估。然后，如果新位置的解质量优于当前位置的解质量，则更新当前位置。如果解决方案的质量高于新解决方案，则NOA模型中的星鸦将保持其当前位置。综上所述，上述概念可以用式(17)表示。最后，NOA伪代码和流程图分别如算法3和图11所示。根据列出的步骤，该算法在Big-O下的时间复杂度为$O(T_{max}N)$。
NOA优点：

• 易实现
• 对于多个具有不同特征的优化问题，能够避免陷入局部最优
• 具有高收敛速度
  NOA局限：
• 无法根据优化问题的需要平衡其探索和开发，以节省计算成本和避免陷入局部最优。

---

总结

提示：这里对文章进行总结：