异常值检测的常用方法简述

目录

异常值定义

为什么进行异常值分析？

常用的异常值检测方法如下

1. 简单的描述性统计分析方法

2. 3原则方法

3. 箱型图分析方法

4. Z-score方法

5. DBSCAN方法

6. 孤立森林（Isolation Forest）方法

---

异常值定义

异常值是指样本中的个别值，其数值明显偏离它（或他们）所属样本的其余观测值。

为什么进行异常值分析？

异常值分析是检验数据是否有录入错误以及含有不合常理的数据。忽视异常值的存在是十分危险的，不加剔除地把异常值包括进数据的计算分析过程中，对结果会产生不良影响；重视异常值的出现，分析其产生的原因，常常成为发现问题进而改进决策的契机。异常值也称为离群点，异常值的分析也称为离群点分析。

常用的异常值检测方法如下

1. 简单的描述性统计分析方法

可以使用python中的pandas库，直接使用describe()来观察数据的统计性描述（只是粗略的观察一些统计量），不过统计数据为连续型的，代码如下：

df.describe()

   loan_amnt   funded_amnt  funded_amnt_inv   installment
count  42535.000000  42535.000000     42535.000000  42535.000000
mean   11089.722581  10821.585753     10139.938785    322.623063
std     7410.938391   7146.914675      7131.598014    208.927216
min      500.000000    500.000000         0.000000     15.670000
25%     5200.000000   5000.000000      4950.000000    165.520000
50%     9700.000000   9600.000000      8500.000000    277.690000
75%    15000.000000  15000.000000     14000.000000    428.180000
max    35000.000000  35000.000000     35000.000000   1305.190000
可以先对变量做一个描述性统计，进而查看哪些数据是不合理的。最常用的统计量是最大值和最小值，用来判断这个变量的取值是否超出了合理的范围。

2. 3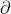原则方法

这个原则有个条件：数据需要服从正态分布。在3∂原则下，异常值如超过3倍标准差，那么可以将其视为异常值。正负3∂的概率是99.7%，那么距离平均值3∂之外的值出现的概率为P(|x-u| 3∂) = 0.003，属于极个别的小概率事件。一组测定值中与平均值的偏差超过两倍标准差的测定值 。与平均值的偏差超过三倍标准差的测定值，称为高度异常的异常值。在处理数据时，应剔除高度异常的异常值。如果数据不服从正态分布，也可以用远离平均值的多少倍标准差来描述。

3. 箱型图分析方法

箱型图提供了识别异常值的一个标准：异常值通常被定义为小于QL－1.5IQR或大于QU＋1.5IQR的值。QL称为下四分位数，表示全部观察值中有四分之一的数据取值比它小；QU称为上四分位数，表示全部观察值中有四分之一的数据取值比它大；IQR称为四分位数间距，是上四分位数QU与下四分位数QL之差，其间包含了全部观察值的一半。

箱型图依据实际数据绘制，没有对数据作任何限制性要求（如服从某种特定的分布形式），它只是真实直观地表现数据分布的本来面貌；另一方面，箱型图判断异常值的标准以四分位数和四分位距为基础，四分位数具有一定的鲁棒性：多达25%的数据可以变得任意远而不会很大地扰动四分位数，所以异常值不能对这个标准施加影响。由此可见，箱型图识别异常值的结果比较客观，在识别异常值方面有一定的优越性，如下图所示。 

 

4. Z-score方法

Z-score是一维或低维特征空间中的参数异常检测方法。该技术假定数据服从高斯分布，异常值是分布尾部的数据点，因此远离数据的平均值。距离的远近取决于使用公式计算的归一化数据点z i的设定阈值Zthr：

                                                                       

其中xi是一个数据点，μ是所有点xi的平均值，δ是所有点xi的标准偏差。然后经过标准化处理后，异常值也进行标准化处理，其绝对值大于Zthr：

                                                                           

Zthr值一般设置为2.5、3.0或3.5。

5. DBSCAN方法

基于DBSCAN聚类方法，DBSCAN是一维或多维特征空间中的非参数，基于密度的离群值检测方法。在DBSCAN聚类技术中，所有数据点都被定义为核心点（Core Points）、边界点（Border Points）或噪声点（Noise Points）。核心点是在距离内至少具有最小包含点数（minPTs）的数据点；边界点是核心点的距离内邻近点，但包含的点数小于最小包含点数（minPTs）；所有的其他数据点都是噪声点，也被标识为异常值；从而，异常检测取决于所要求的最小包含点数、距离和所选择的距离度量，比如欧几里得或曼哈顿距离。

6. 孤立森林（Isolation Forest）方法

该方法是一维或多维特征空间中大数据集的非参数方法，其中的一个重要概念是孤立数。孤立数是孤立数据点所需的拆分数。通过以下步骤确定此分割数：随机选择要分离的点“a”；选择在最小值和最大值之间的随机数据点“b”，并且与“a”不同；如果“b”的值低于“a”的值，则“b”的值变为新的下限；如果“b”的值大于“a”的值，则“b”的值变为新的上限；只要在上限和下限之间存在除“a”之外的数据点，就重复该过程；与孤立非异常值相比，它需要更少的分裂来孤立异常值，即异常值与非异常点相比具有更低的孤立数。因此，如果数据点的孤立数低于阈值，则将数据点定义为异常值。阈值是基于数据中异常值的估计百分比来定义的，这是异常值检测算法的起点。