有关迷宫的生成算法和解密算法

迷宫的基础知识

首先我们需要同步一个观点，即“迷宫是什么？”。在我们的初步认知里，是

定义：能在整个错综复杂的道路中能有一条从起点走向终点的道路

但在此基础上，我们需要强加两个隐藏条件以保证其展示的效果是最佳的，局面是最复杂的，并且每一个迷宫里的格子和墙都是有意义的。

1.每个格子都能被走到

当我们去仔细观察每一张迷宫图其实都能发现，每一个格子都有可能被玩家从起点开始走到，即是有意义的（参考下方两张网图）。

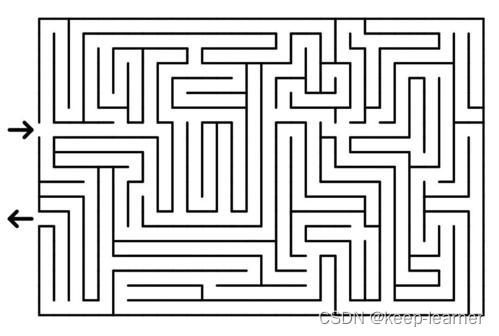
刚开始难以理解，如果偏要设计出一个迷宫，里面有些格子就是专门用来迷惑玩家的，这样难道不行吗？不过思考后会发现其实并没有这种必要。

参考下方的截图（至此之后迷宫的表现形式也多是这种excel表格里的简易版本迷宫）

C是完全不会被走到的区域。可以很快地发现，计算机在玩这种迷宫游戏的时候，完全可以等效于另一种迷宫形式，即不存在C点：

而玩家大多数倾向于一种“深度优先解法”，即一条路走死胡同之后折返回来走另一条路。既然C区域就像是世外桃源一般完全没有办法被访问到，自然也就不会增加折返的任何代价。迷宫的设计思路当然是在有解的前提下越复杂越好，尽量避免冗余信息的存在是迷宫设计的前提之一。

我们为什么不直接把死路的一面墙打通，让走不到的路成为能走到的路，让迷宫变得更有趣呢？

2.除了必要的通路外，没有去除其他的墙

在玩家能解开迷宫的前提下做的尽量复杂，保留足够多的墙也是考虑到的范围之一。

如上面的迷宫，本质意义上来讲在降低复杂度和难度，迷宫的可玩性变得降低。

若迷宫再设计得庞大一些，那么效果更为显著，玩家在面对没有太大挑战性的游戏的时候不会有太大的乐趣（如上图，通路很多，几乎一眼看穿答案，游戏设计简单不复杂），这在游戏设计上是我们不想看到的。

题外话：《游戏设计艺术》一书中p142开始有提到“心流”的概念，玩家在这个状态下显得完全专注于一个活动中，并感到高度的乐趣和满足感。其中很详细地介绍了如果游戏难度一直偏低所带来的影响，其实就是直接处于A1->A2的状态并维持在A2，而因为迷宫算法设计的统一性，很难恢复到A4中。这造成的影响就是玩家难以有心流状态，换句话就是并没有实际地享受这个游戏。

生成算法

在有了以上的两个条件之后，就有了大致的生成思路了。为了达成第二个目标，最简单粗暴的方式就是：无论是哪种初始地图，我们上来就直接用所有的墙堵住所有的格子（当然可以选择留一条起始路径和终末路径），如下图。

第一步都是一样的，接下来就是生成算法的分歧所在了：

那就让我们来看看具体应该如何实现算法，以及研究这些算法生成后的效果。

深度优先算法

我们在大学的时候就有学过类似“深度优先遍历”的概念：从一个节点A开始，不断寻找迭代下一个节点An并以这个节点An开始继续寻找，直到An无法继续，则回退到An-1寻找其他节点Bn。

如这张图的深度优先应当是：1-2-3-4-5-6-7-8-9-10.

那么用到迷宫里该如何使用呢？

1. 选择一个单元格作为当前访问格，并建立一个空栈。

2. 通过当前访问格检查周围是否还有未被访问的单元格。

   1. 如果有，则将当前访问格放入栈中，在周围未被访问的单元格中随机选择一个作为当前访问单元格，打通刚刚的访问格和这时候的访问格之间的墙。

   2. 如果没有，则在栈顶取一个单元格作为当前访问单元格。

3. 直到所有格子都被访问过，即栈空且当前访问格周围都被访问过。

让我们直接来看简易流程：

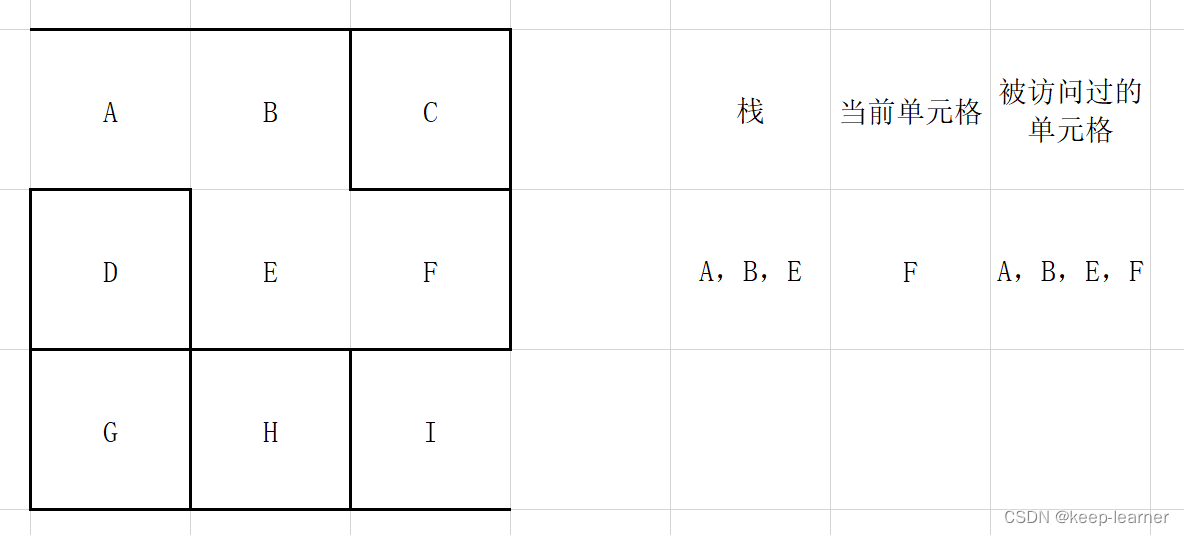
注意，这一步之后，当前单元格周围的单元格都被访问过，所以从栈顶弹出之前的那些格子G->H->I->F，直到下一个周围没有全部被访问到的单元格出现（F）。

之后全部弹栈，被访问过的单元格已经是全部单元格了，所以没有必要再消除墙。至此一个迷宫就生成了。

想法：因为是深度优先，所以可以很明显地感觉到，由于后面被访问到的格子优先级最高，由它来决定新的路径该往哪走，导致了越是刚开始被访问到的点，后面返工的时候周围的路径几乎被先前访问到了，才越不可能被再次用来拓展其他路。有了优先级，这个算法才适合生成一条主干路，途中生成的其他路为辅路的地图，也就是我们常提到的“主线和支线”的概念。

prim最小生成树算法

prim生成树算法的一个简易理解就是：每次从“最周边的，将要被访问但还没被访问到”的节点中随机选择一个进行访问，同时把这个节点周围还没被定义成“最周边的，将要被访问但还没被访问到”的节点定义成此，直到所有节点都已被访问到。

在迷宫里的具体操作方式是：

1. 选择一个单元格作为当前访问格，并建立一个集合，作为“已访问过但周边仍然有没访问过的格子”的集合。将第一个访问格放入集合中

2. 从集合中随机选择一个访问格，检查它的四周是否还有未被访问过的格子。

   1. 如果有，则随机选择一个它周边未被访问过的格子进行访问，打通这两个格子中的墙壁，并将这两个格子都重新放入集合中。

   2. 如果没有，则弃用此访问格，不放回集合中。

3. 直到所有格子都被访问过，即集合为空。

这么说有点过于概括，很难解释清楚，所以直接走流程。

每次都从集合中随机选择一个单元格来检查四周，比如上图这里再选择A的时候就只剩下D作为唯一的选择来打通了。

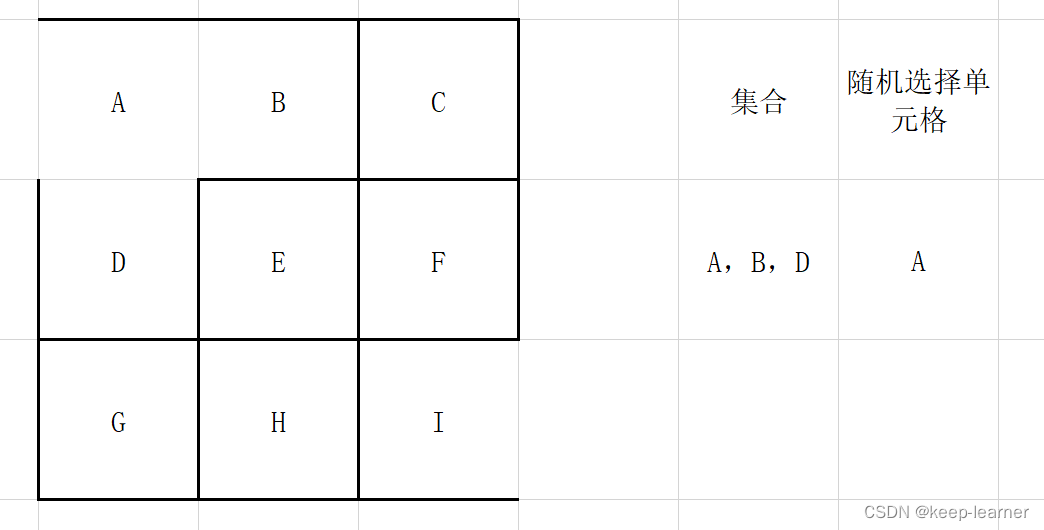
上图这次仍然选择A的话，已经发现四周没有其他没被访问过的单元格了，所以从集合中删除，并且重新随机选择。

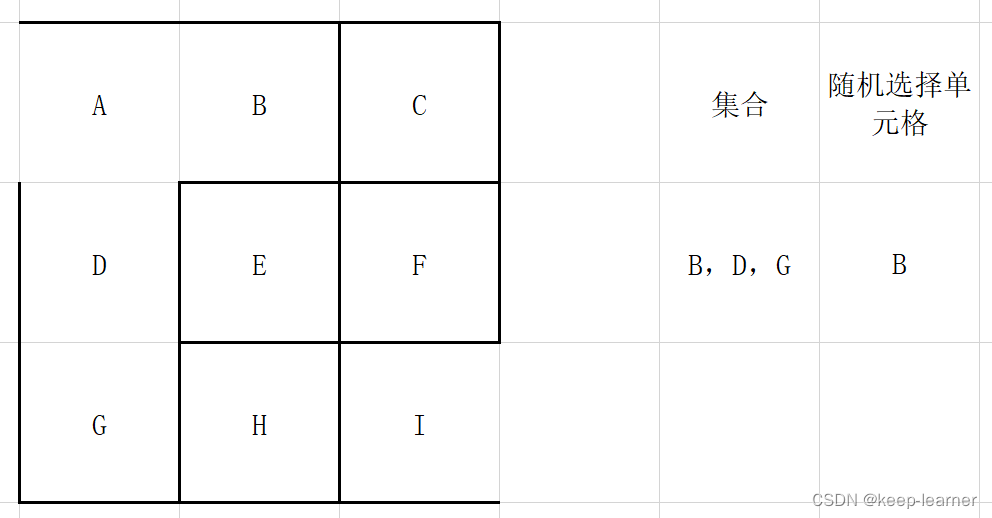
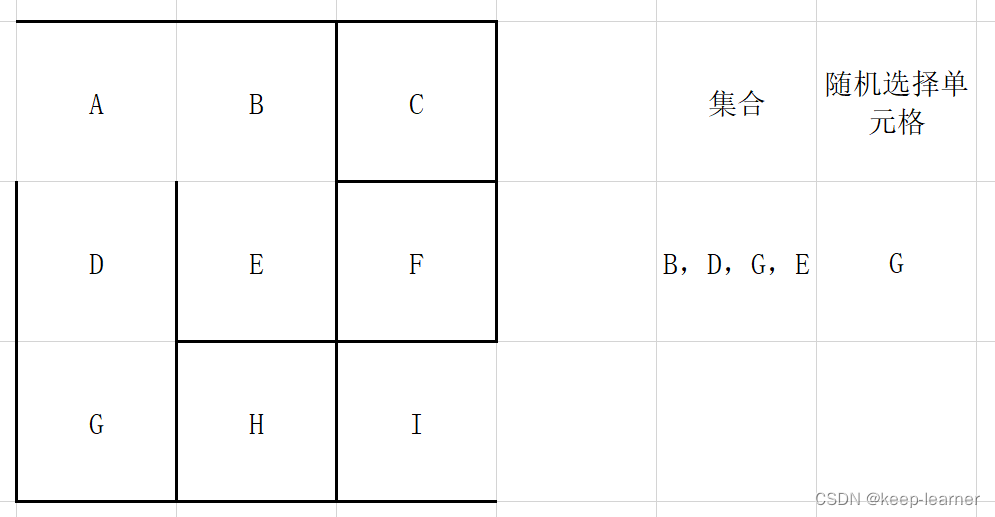
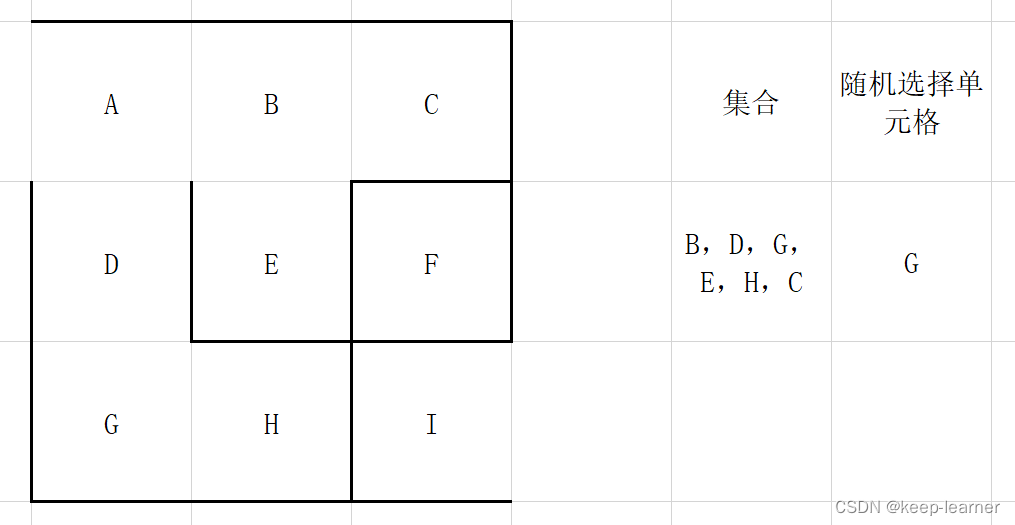
可以看到上图，又随机选到周围都被访问过的单元格了，还是和A一样，直接从集合中去掉，重新随机选择。

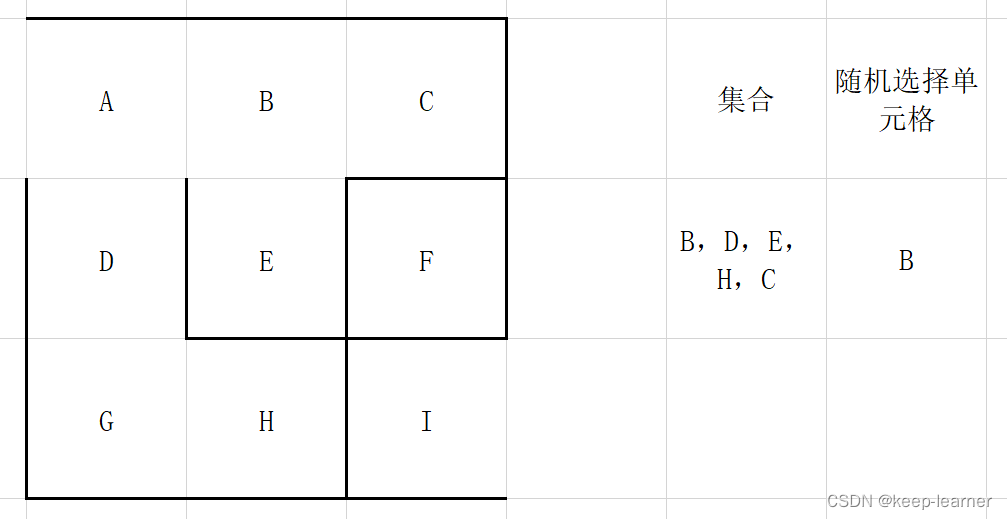
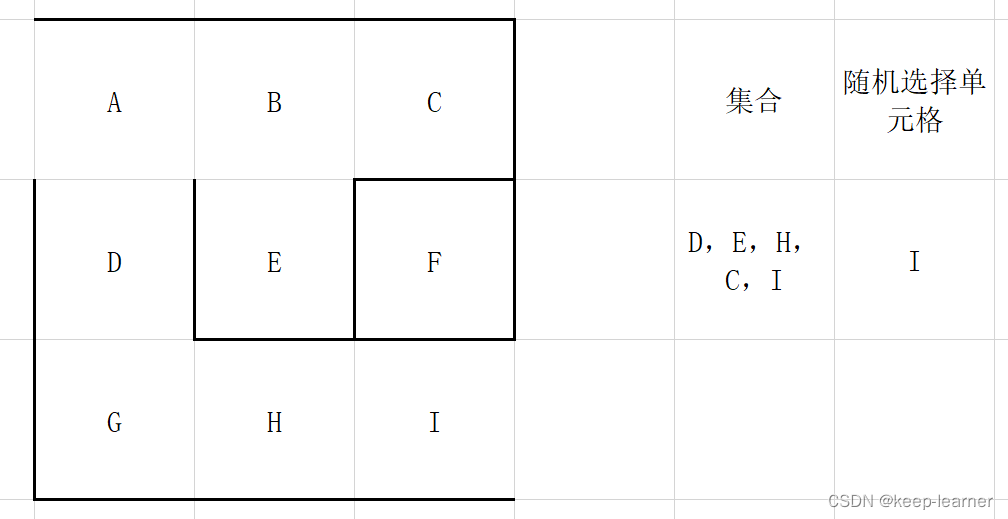
可以看到所有的单元格都访问过了，那接下来的循环就都是逐个删除集合中的元素。

......

效果：

想法：因为它无论是在找已访问过的节点，还是在打通墙壁前找没访问过的节点，都是公平随机的，所以相对于其他两种算法来讲，迷宫复杂度最高，最需要玩家的策略解开。所以是目前最适合用于纯迷宫题材的游戏。

思考

有没有一种方式，让我们打破常规逻辑，在刚开始的时候不生成所有的墙，但依然符合迷宫的第二个条件呢？

新坑：递归分割算法

解密算法

以子之矛，陷子之盾。既然想到了生成，就再想想解密的事情。之前学习《算法与数据结构》的时候就有了解过树的深度优先遍历和图的最短路径，都有助于对迷宫的解密算法的理解。

深度优先算法

即使是玩家也多数会采用这样的一个策略：走一条路走到底，直到这条路是死路，则折返到第一个交界区，重新做其他选择。

具体在迷宫里这么操作：

1. 选择一个单元格作为当前访问格，并建立一个栈保存路径。

2. 通过当前访问格来找到附近没有被访问过的单元格。

   1. 如果附近有没被访问过的单元格，则将当前访问格放入栈中，在周围未被访问的单元格中随机选择一个作为当前访问单元格。

   2. 如果附近并未发现没被访问过的单元格，则弃用此访问格，不放回栈中。取栈顶的那个单元格作为当前访问格。

3. 直到访问到了终点。

4. 从栈顶到栈底的路程就是从终点到起点的路程。

可以很清楚地看出来，解密算法中的深度优先和生成算法中的深度优先几乎一致，只不过跳出循环的条件由“栈空”变为了“访问到了终点”接下来看看图示流程。

（有颜色代表访问过，绿色代表访问过且还在考察中，红色代表访问过但是是之前折返的死路）

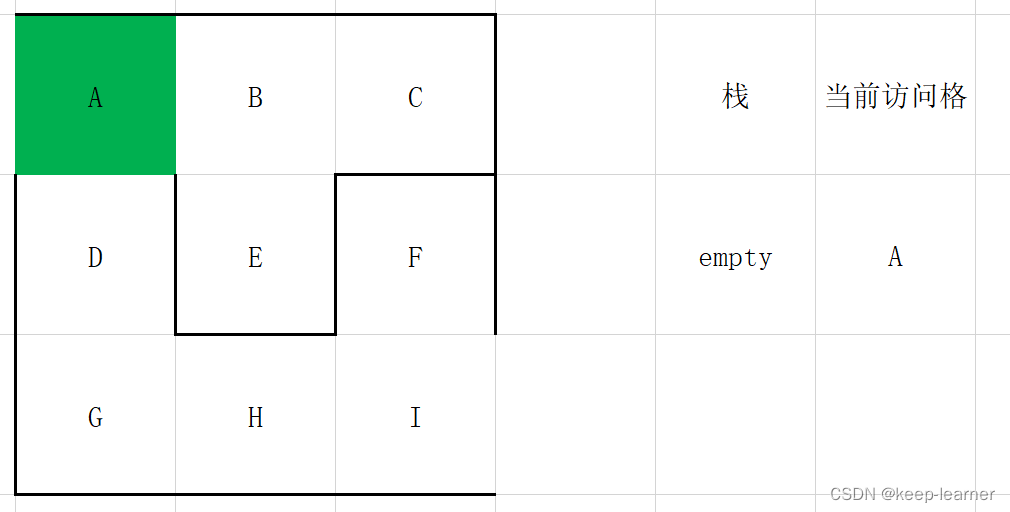
这里发现C周围没有任何通路了，则退回到B点，即弹栈。

这时候退到B点，同时B再次搜寻周围，发现也都被访问过了，所以再次退回到A点。

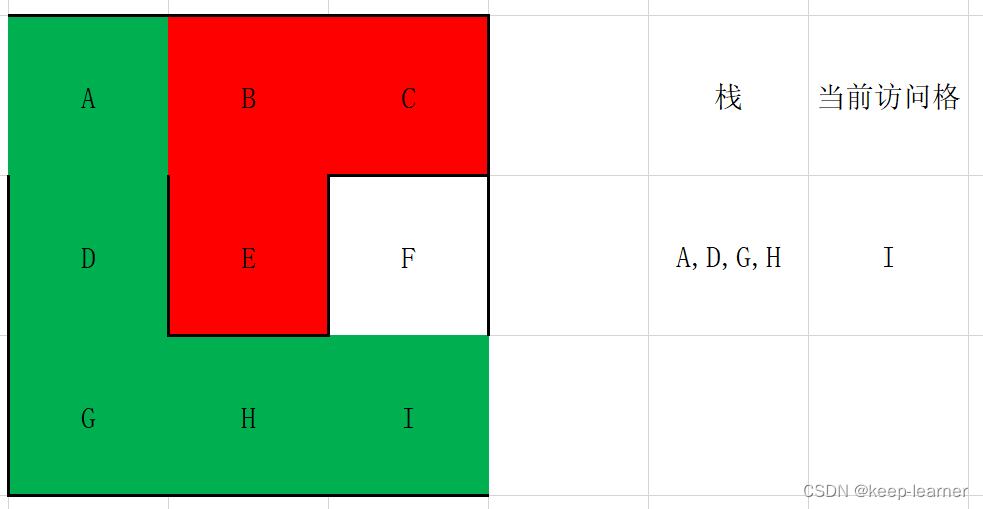
这时候访问到终点了。所以I->H->G->D->A就是从终点到起点的过程。

A*寻路算法

A*寻路算法属于启发式搜索算法，就是在状态空间中的搜索对每一个搜索的位置进行评估，得到最好的位置，再从这个位置进行搜索直到目标。这个算法多多少少有些玄学（定理在没有读懂证明前都会觉得是玄学），我暂时没有想通证明过程，只能复现整个算法流程。

新坑：A*寻路算法的证明。

前置知识：现在每个格子都会有三个值：

1. G：从起点到这个点的最短距离。因为我们刚开始是从起点开始探寻的，所以刚开始的G值或许只是暂时的最短距离值，说不定走到后面发现还要继续更新。这个值是不固定的，动态更新的值，随时会因为找到更好的值而被替换掉。

2. H：从这个点到终点的曼哈顿距离。

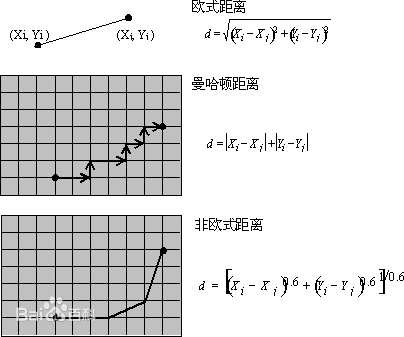
简单理解曼哈顿距离就是，在方块图中，只有起点和终点，不允许斜着走，只允许直走所需要的步数。

1. F：代价值。F=G+H。因为G是会随着步骤的进行而更新，所以F值也有可能会被更新。

好了，接下来就开始讲讲算法的具体流程：

1. 创建一个用于存储周边未访问格子的集合。

2. 进行循环

   1. 选择起点作为当前访问格（起点的G值为0，H为到终点的曼哈顿距离）。

   2. 搜索当前访问格周围（上下左右）的格子。做如下判断：

      1. 如果这个格子之前被访问过或者被墙阻隔，那么忽略它，不做考虑。

      2. 如果这个格子没有被访问过，且没被墙阻隔，且没有在集合中，那么就可以计算它的G值和H值。H值很好计算，终点是固定的，那么就由当前格子的坐标和终点坐标之间做曼哈顿差值即可。G值就是当前访问格子的G值加上1就行（从起点到当前访问格的距离+1=从起点到这个未被访问过的格子的距离）。

      3. 如果这个格子没有被访问过，且没被墙阻隔，且在集合中，那么就可以试探G值是否需要更新。也就是，之前的G值，与现在的这个当前访问格的G值+1做对比（是否是当前访问格走到这个格子的路径最短），如果是则把父节点指向这个当前访问格，不是则不用更新父节点。

   3. 更新当前访问格为集合中F值（F=G+H）最小的格子。

3. 结束循环直到走到终点格子。

4. 从终点循着父节点一直走到起点的路程就是通路。

接下来我们来看图示流程：

在这里D和G的F值都一样为5，我们随机选择一个作为当前访问格。

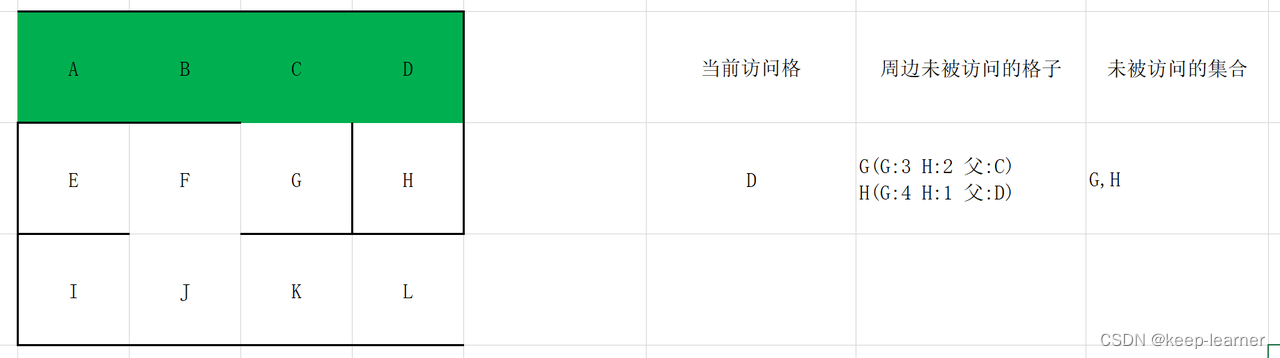
随机选择G，H。

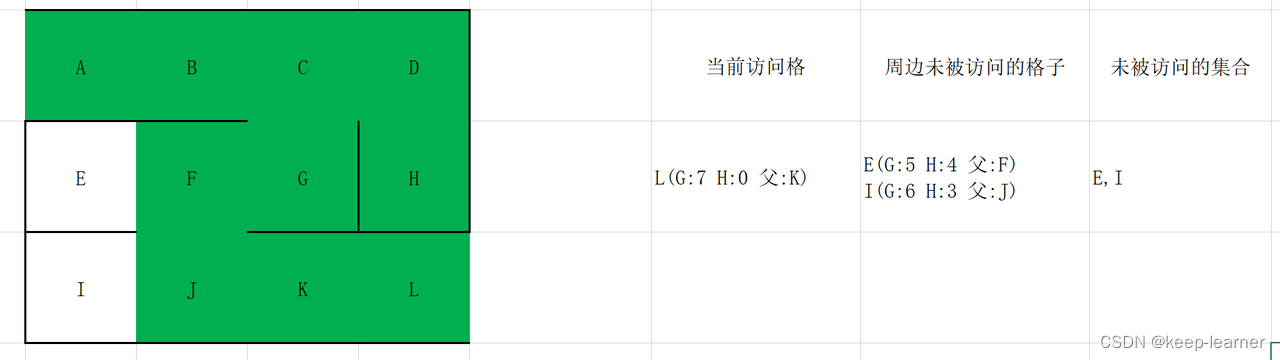
至此结束了整个流程。从L开始递归往回找父节点直到起点：L->K->J->F->G->C->B->A.

想法：图示示意了什么？有哪些理论上步骤实际上我们并没有使用到？

没错，在学习了A*寻路算法和迷宫的定义之后，我们很快就能发现有些变量实际上根本没有任何作用。比如G值，本质上是为了优化最佳路线而存在的值，在迷宫中因为不存在多条通路，所以根本没有更新过；F值只有在选择下一次访问格的时候做了个优先级判断罢了（从上面E和I没有被选择可以看出，优先级低的没有被选择到，可以少走一些循环判断），实际上并没有太大作用。

由此，我们想想，这个算法在解决迷宫问题上有没有优化的空间？

广度优先算法（自命名）

如果仔细观察思考，我们就会发现，A*寻路算法其实更多的是在有更多通路的情况下寻找到最优解的算法，类似于帝国时代2和英雄联盟的人物导航系统。

但我们迷宫的定义本身就是只有一条通路啊，从起点到地图里的每一点，都只有一种走法，那是不是就可以免去A*寻路算法里面那么多没必要的参数，只需要保证父节点就好了呢？答案是对的。

所以我们就可以有如下几步：

1. 创建一个用于存储周边未访问格子的集合。

2. 进行循环

   1. 选择起点作为当前访问格。

   2. 搜索当前访问格周围（上下左右）的格子。做如下判断：

      1. 如果这个格子之前被访问过或者被墙阻隔，那么忽略它，不做考虑。

      2. 如果这个格子没有被访问过，且没被墙阻隔，则把它放入到集合中，并将它的父节点设置为当前访问格，

   3. 更新当前访问格为未被访问的周边格子集合中随机一个格子。

3. 结束循环直到走到终点格子。

4. 从终点循着父节点一直走到起点的路程就是通路。

随机选择D或G。

至此访问到了终点。从终点开始往其父节点递归至起点，L->K->J->F->G->C->B->A，就是整个解密流程。

想法：可以看到，A寻路算法可以有效地避开一些废点，比如上面的E和I，但是广度优先算法（自命名）不能保证，因为下一次的访问格是随机取的，可能会取到我们并不需要的格子。但广度优先算法简化了很多没必要的操作（比如计算F，G，H值），更容易被理解和接受。所以在解决迷宫这类问题的时候，我还是倾向于用广度优先算法而非A寻路算法。

思考

现在在广度优先遍历和深度优先遍历中选择，你认为哪种方式更好呢？