VLN小知识积累

本文回顾一些基本知识
（主要写给自己看的，力争用最简洁明了的语言解释这些基本概念）
不断更新

1，betweenness centrality（中介中心性）

中介中心性参考

graph中某个节点的中介中心性计算公式：

g(v) 代表顶点 v 的Betweenness Centrality值。
${\sigma }_{st}(v)$代表从顶点s到顶点t之间经过v的最短路径数。
${\sigma }_{st}$代表从顶点s到顶点t之间所有的最短路径数。

• 如果两个节点是s，t之间有最短路径，但是不经过v，则${\sigma }_{st}(v)$=0，如下图${\sigma }_{BF}(C)$=0。
• 也就是说，我们只考虑两点之间的最短路径，${\sigma }_{st}(v)$与${\sigma }_{st}$之间的区别是是否经过v，而不是是否是最短。由于${\sigma }_{st}(v)$=0，计算v的中介中心性时我们不考虑不经过点v的路径。
• 步骤：找到最短路径和经过该点的所有路径数量相除，最后再将所有结果相加。

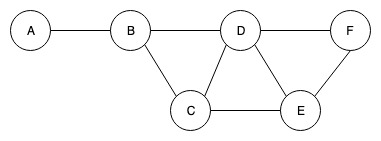
以上图为例，我们计算B的中介中心性：

要计算某个顶点的中介中心性，肯定要遍历graph中所有经过该点的路径（和最短路径），为了清晰不遗漏所有路径地进行遍历，我们分别从不同顶点出发遍历所有路径

• 路径：ABD，ABC，ABDF，（ABDE，ABCE）
• 从B点出发没有经过B点的路径
• 类似的遍历其他路径：CBA，DBA，（EDBA，ECBA），FDBA

其中，${\sigma }_{AE}(B)$=2, ${\sigma }_{AE}$=2 ，因为有（ABDE，ABCE）。${\sigma }_{EA}(B)$=2, ${\sigma }_{EA}$=2 ，因为有（EDBA，ECBA).

2，风险最小化（Empirical Risk MinimizationERM）

风险最小化参考

概率和似然的区别

概率(probability)和似然(likelihood)，都是指可能性，都可以被称为概率，但在统计应用中有所区别。

概率(probability)：用于在已知模型的情况下预测新的数据。
例如：抛一枚匀质硬币，抛10次，6次正面向上的可能性多大？东西（模型）已经确定，求事情（数据）发生的概率

**似然(likelihood)：**给定已知数据来拟合模型，或者说给定某一结果，求某一参数值的可能性。根据事情
例如：抛一枚硬币，抛10次，结果是6次正面向上，其是匀质的可能性多大？

极大似然估计MLE：

假设一个袋子里有不知道多少个编号为1和2的球，样本x的分布如下：

x	1	2
P	θ	1-θ

依次取出小球为：1，1，2，1，2
那么其似然函数就是 L(θ) =θθ(1-θ)θ(1-θ) = ${\theta }^3(1-\theta {)}^{\theta }$
我们要求使得这个函数 L(θ) 最大的 θ值，
通常求法是，取对数ln然后求导得到极大值。上面例子的结果为3/5.
最大似然估计更常见的是求正态分布的均值与方差。

最大后验概率

在最大似然估计中，我们并没有考虑p(θ)，即我们假设θ是一个固定值，但实际上，参数θ可能并不是固定的，它只是取某些值可能性比较大。因此我们只要将似然函数乘以先验概率然后取最大即可。最大后验概率：

$p(\theta |X)=\frac{p(X|\theta )\times p(\theta )}{{\sum }_{{\theta }_i}p(X|{\theta }_i)\times p({\theta }_i)}$

这里的p(θ)是参数θ的先验概率，p(θ|X)是后验概率，而p(X|θ)就是我们上面提到的似然函数。

期望：
平均数是统计学概念，期望是概率论概念。
平均数是 实验后 根据实际结果统计得到的样本的平均值；
期望是 实验前 根据概率分布“预测”的样本平均值。
期望：
离散型
期望的定义是$E(X)={\sum }_{i=1}^n{x}_{i}p(x_i)$,即每个值$x_i$乘上它出现的概率 $p(x_i)$
连续型
$E(X)=x\ast p(a,b)=x\ast {\int }_b^{a}f(x)dx={\int }_{-\infty }^{\infty }x\ast f(x)dx$

期望风险
损失函数度量一次预测的好坏，风险函数度量平均意义下模型预测的好坏。
损失函数值越小，模型越好。损失函数的期望是：

$R_{exp}(f)=E_p[L(Y,f(X))]=\int L(y,f(x))P(x,y)dxdy$

这是理论上模型$f(x)$,关于联合分布$P(X,Y)$的期望损失，称为期望风险。

经验风险
联合分布$P(X,Y)$是未知的，期望风险不能直接计算，期望风险$R_{e}xp(f)$可以近似为 $f(x)$ 关于训练数据集的平均损失，也就是经验风险（empirical risk），即：

$R_{emp}(f)=\frac{1}{N}{\sum }_{i=1}^{N}L(y_i,f(x_i))$

根据大数定律，当样本容量N趋于无穷时，经验风险$R_{emp}(f)$趋于期望风险 $R_{exp}(f)$。但是现实中训练样本数目有限，用经验风险来估计期望风险往往并不理想，要对经验风险进行一定的矫正，也就是形成结构风险.

风险最小化

经验风险最小化（empirical risk minimization,ERM）
经验风险最小化的策略认为，经验风险最小的模型是最优的模型：

$\underset{f\in F}{\min }\frac{1}{N}{\sum }_{i=1}^{N}L(y_i,f(x_i))$

当样本容量足够大时，经验风险最小化能保证有很好的学习效果。比如，极大似然估计（就是经验风险最小化的一个例子，当模型是条件概率分布，损失函数是对数损失函数时，经验风险最小化就等价于极大似然估计。
但当样本容量很小时，经验风险最小化容易导致“过拟合”。

结构风险最小化

结构风险最小化（structural minimization, SRM）是为了防止过拟合提出的策略。结构风险最小化等价于正则化（regularization）。结构风险在经验风险上加上表示模型复杂度的正则化项（regularizer）或罚项（penalty term）。结构风险的定义是

$\underset{f\in F}{\min }\frac{1}{N}{\sum }_{i=1}^{N}L(y_i,f(x_i))+\lambda J(f)$

其中，J(f)是模型复杂度的函数，$0\le \lambda$是系数，用来权衡经验风险和模型复杂度。

结构风险最小化的策略认为结构风险最小的模型是最优模型：

$\underset{f\in F}{\min }\frac{1}{N}{\sum }_{i=1}^{N}L(y_i,f(x_i))+\lambda J(f)$

结构风险小需要经验风险和模型复杂度同时都小，结构风险小的模型往往对训练数据以及未知的测试数据都有较好的预测。

比如，贝叶斯估计中的最大后验概率估计（maximum posterior probability estimation,MAP）就是结构风险最小化的一个例子，当模型是条件概率分布、损失函数是对数损失函数、模型复杂度由模型的先验概率表示时，结构风险最小化就等价于最大后验概率估计.

临域风险最小化（Vicinal Risk MinimizationVRM）

上面的经验风险最小化通常会面临过拟合，处理这种问题的方法除了正则化还有数据增广。VRM正是这种方法，网上仔细分析VRM的文章不多，下面直接介绍更简单有效的方法mixup;

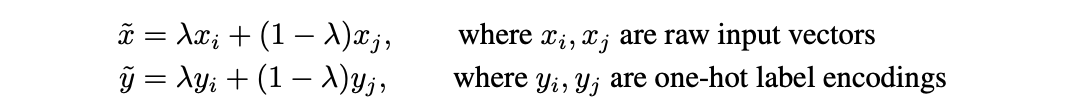
其中 λ ∈ [0,1]。其中λ ~Beta(a,a), a 属于(0, ∞)

1.三个或以上的样本进行mixup并不会带来更多的收益。
2.模型容量越大或者训练时间越长mixup带来的收益越多。

VRM(Vicinal Risk Minimization)原则跟ERM原则在思想上类似，核心不同点在于训练样本的构建。在ERM每一个原训练样本基础上，VRM需要人根据先验知识为每一个原样本描述一个领域，领域是由相似但又不同于原训练样本的样本组成的集合， 最后额外的样本从每一个原样本的领域中抽取出来来扩充整个训练样本集，这就是我们所说的data augumentation。在图像分类中领域的构建可以通过翻转， 旋转，缩放原样本。经过扩充的训练集可以提高模型的泛化能力， 但是如何通过data augmentation扩充数据集，和使用什么样的data augmentation方法是原训练集相关的和需要先验知识的。而且我们以上所提到的data augmentation方法所产生的新的样本都跟原样本属于同一个类别，并没有建模不同类别样本间的临近关系。 所以mixup作为一种简单的和数据集不相关的data augmentation方法在这种情况下被提出了。 Mixup足够简单

mixup官方参考代码

criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=args.lr, momentum=0.9,
                      weight_decay=args.decay)

def mixup_data(x, y, alpha=1.0, use_cuda=True):
    '''Returns mixed inputs, pairs of targets, and lambda'''
    if alpha > 0:
        lam = np.random.beta(alpha, alpha)
    else:
        lam = 1

    batch_size = x.size()[0]
    if use_cuda:
        index = torch.randperm(batch_size).cuda()
    else:
        index = torch.randperm(batch_size)

    mixed_x = lam * x + (1 - lam) * x[index, :]
    y_a, y_b = y, y[index]
    return mixed_x, y_a, y_b, lam


def mixup_criterion(criterion, pred, y_a, y_b, lam):
    return lam * criterion(pred, y_a) + (1 - lam) * criterion(pred, y_b)


def train(epoch):
    print('\nEpoch: %d' % epoch)
    net.train()
    train_loss = 0
    reg_loss = 0
    correct = 0
    total = 0
    for batch_idx, (inputs, targets) in enumerate(trainloader):
        if use_cuda:
            inputs, targets = inputs.cuda(), targets.cuda()

        inputs, targets_a, targets_b, lam = mixup_data(inputs, targets,
                                                       args.alpha, use_cuda)
        inputs, targets_a, targets_b = map(Variable, (inputs,
                                                      targets_a, targets_b))
        outputs = net(inputs)
        loss = mixup_criterion(criterion, outputs, targets_a, targets_b, lam)
        train_loss += loss.data[0]
        _, predicted = torch.max(outputs.data, 1)
        total += targets.size(0)
        correct += (lam * predicted.eq(targets_a.data).cpu().sum().float()
                    + (1 - lam) * predicted.eq(targets_b.data).cpu().sum().float())

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

beta分布

可以看到，概率密度函数是对称的，α = 1时，B e t a ( α , α ) 成了均匀分布

当 α → 0 ，Beta 的概率密度函数趋向于0，抽样时 λ → 0 ，mixup 融合没有了，VRM 回退成 ERM

当 α → ∞ ，Beta 的概率密度函数趋向于 ∞

参考

掩蔽语言建模Masked Language Modeling (MLM)、掩蔽区域建模Masked Region Modeling (MRM)和指令轨迹匹配 Instruction Trajectory Matching (ITM)。

3，交叉熵

softmax

input = torch.tensor([[[[0.5546, 0.1304, 0.9288],
                        [0.6879, 0.3553, 0.9984],
                        [0.1474, 0.6745, 0.8948]],
		               [[0.8524, 0.2278, 0.6476],
                        [0.6203, 0.6977, 0.3352],
                        [0.4946, 0.4613, 0.6882]]]])
target = torch.tensor([[[0, 0, 0],
                       [0, 0, 0],
                       [0, 0, 1]]])
# cross_entropy的实现               
loss = F.cross_entropy(input, target)
print(loss)

# 利用nll_loss实现cross_entropy
input = F.softmax(input, dim=1)
input = torch.log(input)
# input = F.log_softmax(input, dim=1)  # 上面的两行代码和这个是等价的
loss = F.nll_loss(input, target)
print(loss)

f.null(x,y)

loss(input,class) = -input[class]
例如，input=[该样本被预测为第一类分数，第二类的分数，第三类的分数]=[-1.23, 2.56, 0.56], 实际应该是第三类class=2，nll_loss = 0.56
也就是说这是一个三分类任务，对于这个样本，损失函数nll取这个样本的实际分类位置的负数作为损失，试想一下，0.56也就是预测值越大，损失越小，也就是预测越准，越不用降低损失。
softmax一是模拟了max，还可导，而且按概率来说，每个分类的概率和要为1.

4，编码-解码

机器翻译是序列转换模型的一个核心问题， 其输入和输出都是长度可变的序列。 为了处理这种类型的输入和输出， 可以设计一个包含两个主要组件的架构： 第一个组件是一个编码器（encoder）： 它接受一个长度可变的序列作为输入， 并将其转换为具有固定形状的编码状态。 第二个组件是解码器（decoder）： 它将固定形状的编码状态映射到长度可变的序列。
原文链接：https://blog.csdn.net/flyingluohaipeng/article/details/125605257

5，预训练-微调

在相对上游的任务上进行训练，在下游任务上微调。

6，强化学习与模仿学习（学习更新中，，，）

IL+RL论文（CVPR2019best student paper）
b站视频
强化学习

强化学习简介

马尔可夫决策

模仿学习与行为克隆
参考1

参考2

蒙特卡洛

A3C

其实行为克隆和监督学习一样的。它的思路就是完全复制专家的行为(克隆)，专家怎么干它就怎么干。
  这种方法大多数情况下没有问题，但行为克隆会有问题。

问题一：特殊情况
  但专家的观测也是有限的。举个例子就是司机不会在能拐弯的时候去撞墙，所以对于撞墙下面的状态就没有示范了。但有的时候机器学习的时候会随机进入这种状态，无法处理。所以只观察专家行为是不够的，需要招数处理这种特殊情况。这个招数就叫做数据集聚合。
  希望收集更多样化的数据，并且包含最极端的情况。数据集聚合的思想很野蛮，就是让专家也处于这种极端的情况(我感觉说了和没说一样)，有了这样的数据就能够进行处理了。

问题二：会跑偏
  除了上面的问题，行为克隆还有一个问题就是可能学不到点子上。比如专家有多种形式的知识，本来想学习知识1，但实际学了知识2，而且内存空间有限，学完了知识2满了。这就彻底跑偏了。

问题三：有误差
  在学习过程中，很难和专家一摸一样。但RL中是前面状态会影响到后面状态的。监督学习中独立分布没有问题，但这个里面可能就会越走越偏。

模仿学习结合强化学习
模仿学习的特点：

• 用人工收集数据往往需要较大成本，而且数据量也不会很大，并且存在数据分布不一致的问题。 人也有很多办不到的策略，如果是非常复杂的控制（例如高达机器人，六旋翼飞行器），人是没办法胜任的。 训练稳定简单。最多只能做到和示教数据一样好，无法超越。

强化学习的特点：

需要奖励函数。
需要足够的探索。
有可能存在的不能收敛问题。
可以做到超越人类的决策。
因此我们可以把两者结合起来，既有人类的经验，又有自己的探索和学习。我们的做法是进行预训练和微调。AlphaGo正是运用了这种框架。同样星际争霸2的AlphaStar同样也是这种训练框架，得到了超越人类的水平。

模仿学习和强化学习可以结合互补使用得到更好的实验结果：模仿学习（行为克隆）是一步一步地跟随学习，只能学习有限的具体的行为。相反，强化学习可以通过奖励函数进行总体学习，不局限于具体的动作。但是至少在VLN任务中，没有局部的奖励函数，只有最后任务成功才会奖励，就可能造成不收敛（乱学习）。