【算法】分治法详解和汇总

概述

分治法的设计思想

分治法的基本思想是将一个难以直接解决的大问题划分为一些规模较小的子问题，分别求各个子问题，然后将各个子问题的答案合并成为规模较大的原问题的解。一般来说，分治法的求解过程由以下三个阶段组成：

• 划分：把规模为n的原问题划分为k个规模较小的子问题
• 求解子问题：各个子问题的解法和原问题的解法通常是相同的。可以用递归的方法求解各个子问题，某些情况下递归可以转化为循环
• 合并：把各个子问题合并起来，合并的代价因为情况不同有着很大的差异，因此分治法算法的效率很大上取决于合并的实现。

在用分治法设计算法的时候，最好使得子问题的规模大致相同。也就是将一个问题的划分称为规模相等的k个子问题，这种使得子问题规模大致相等的做法是出自一种平衡子问题的启发性问题。 另外，在使用分治法设计算法的时候，最好使得各个子问题之间相互独立，如果各个子问题不是独立的，那么分治法会求一些重复求解的重叠子问题，这会导致做很多重复工作，使得算法的效率下降，此时使用动态规划算法更好。

排序问题中的分治法

归并排序

** 归并排序基本思想**
什么是归并：将两个或者多个已经有序的序列合并成一个。比如n个有序序列，只需要不断对比这些序列的头部，选出其中最小元素放入新数组，那么最后将获得一个有序的新数组。将n个有序序列归并成为n路归并

归并排序的基本思路：
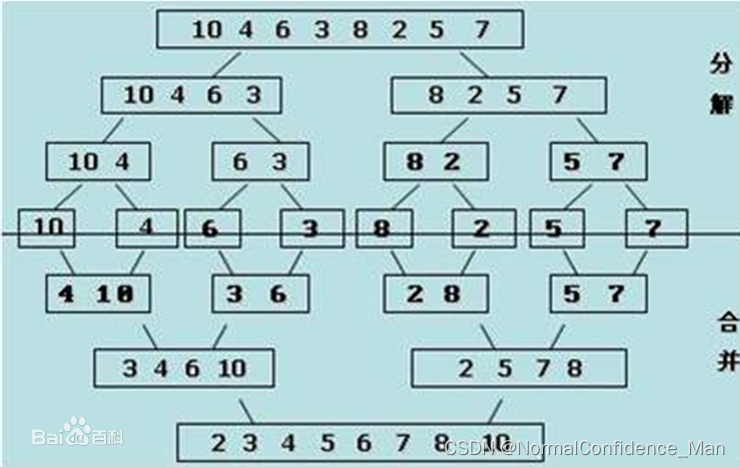
归并排序首先执行划分过程，将序列划分为两个子序列，如果子序列的长度为1，则结束划分，否则继续执行划分。直到将具有n个元素的序列划分为n个长度为1的子序列，我们可以将这些子序列看作是有序的。然后这些子序列进行两两合并并进行排序，得到若干个长度为2的有序子序列；接下来则继续进行两两合并，得到若干个长度为4的子序列。重复上述操作，直到只剩下一个长度为n的序列，此时的序列是有序的

代码实现

// 归并排序
int *b= (int *)malloc(n*sizeof(int));   // 辅助数组

// 一趟归并
// 每一趟的a[low...mid]和a[mid...high]是有序的
void mergeSort(int a, int low, int mid, int high){
    int i,j,k;
    for (k = low; k <= high; ++k) {
        b[k]=a[k];  // 复制a到b中
    }
    for (i = low, j=mid+1, k=i; i<=mid && j<=high; k++) {
        if (b[i]<=b[j]){    // 如果左指针的值小于右指针的值
            a[k]=b[i];      // 放入左指针的值
            i++;
        }else{
            a[k]=b[j];
            j++;
        }
    }
    while (i<=mid){a[k++]=b[i++];}
    while (j <= high){a[k++]=b[j++];}
}

void mergeSort(int a[], int low, int high){
    if (low<high){
        int mid=(low+high)/2;
        mergeSort(a,low, mid);  // 将左边排序
        mergeSort(a, mid+1, high);  // 将右边排序
        merge(a, low, mid, high);   // 一趟归并
    }
}

算法性能分析
归并排序很像一个倒立的二叉树，称之为归并树

设顺序表中有n个元素的乱序顺序表，如果归并树树高为h，则$n\le 2^{h-1}$。归并树高代表着其归并的趟数，每一趟归并的时间复杂度为O(n)，因为每一趟最多需要进行n-1次比较，最少需要进行n/2次比较，因此，算法时间复杂度为$O(nlo{g}_{2}n)$

空间复杂度为O(n)，主要来自于辅助数组。

该算法是稳定的

快速排序

基本思想
快速排序的基本思想是分治法。在待排序列L[1…n]中选择任意元素pivot作为枢轴，然后将大于pivot的元素放置在pivot右边，将小于pivot的元素放置在pivot左边，形成L[1…k-1]和L[k+1…n]两个子序列。快速排序算法会递归地对划分出来的两个子序列L[1…k-1]和L[k+1…n]递归地重复上述过程，直到每个子序列中只有一个元素或者直接为空为止。

具体过程：

• 划分：选定一个记录作为枢轴，以枢轴为基准将整个序列划分为两个子序列。并且前一个子序列中的记录都小于或者等于枢轴，后一个子序列都大于枢轴。
• 求解子问题：分别对划分后每一个子序列进行递归
• 合并：合并不需要进行任何操作，因为排序是原地进行的。

代码实现

// 快速排序
int partition(int a[], int low, int high){
    int pivot = a[low]; // 将第一个元素作为枢轴
    while (low<high){
        while (low<high && a[high]>=pivot) --high;
        a[low]=a[high]; //如果右端找到比枢轴小的，则将元素移动到枢轴左端
        while (low<high && a[low]>pivot) ++low;
        a[high]=a[low]; //如果左端找到比枢轴大的，则将元素移动到枢轴右端
    }
    a[low] = pivot; // 当low==high的时候遭到枢轴的位置了
    return low; // 返回枢轴最终位置
}

void quickSort(int a[], int low, int high){
    if (low<high){  // 递归结束条件：如果low>=high，那么本次递归就结束了
        int pivot = partition(a,low,high);  //确定pivot位置
        quickSort(a, low, pivot-1); // 排序pivot左侧
        quickSort(a, pivot+1, high);// 排序pivot右侧
    }
}

快速排序算法性能
空间效率：由于快速排序是递归的，因此需要一个递归工作栈来保存每层递归调用的必要信息，其容量与递归调用的最大深度一致。最好的情况下，递归呈现为平衡二叉树状，为O(log₂n)；最坏情况发生在两个区域分别包含0和n-1个元素的时候，这种最大程度的不对称性若发生在每层递归上，则最坏情况深度为O(n)。

时间效率：在快速排序中，产生时间的主要是Partion函数和递归函数QuickSort，对于Partion函数，其需要的时间复杂度为O(n)，而对于QuickSort函数，其执行次数和递归深度有关，根据空间效率可知，最好的情况下，递归呈现为平衡二叉树状，为O(log₂n)；最坏情况栈深度为O(n)，因此，最坏时间复杂度为O(n²)；当刚好平衡划分的时候，最好的时间复杂度为O(n)。

为了提高算法效率，应该尽可能的将数据中间值选作枢轴，但是又不值得为此遍历一次序列。因此可以在序列头，序列尾和序列中各选取一个元素，再从这三个元素中取中值，或者直接随机取一个元素，都可以降低最坏情况发生的概率。

在最理想的状态下，快速排序刚好平衡划分，这种情况下快速排序的运行速度将大大上升。好在快速排序平均情况下的运行时间与其最佳情况下的运行时间相近，也是O(nlog₂n)，因此快速排序是所有内部排序算法中平均性能最优的算法。另外，快速排序是不稳定的。

TIPS：一趟排序表示的是一层quickSort的结果，一趟排序可以确定多个元素的位置

组合问题中的分治法

最大子段和问题

问题描述：
给定n个整数（存在负数）组成的序列，最大子段和问题要求在该序列中取一个连续的子序列，并且确保该子序列的和是序列中最大的。比如说序列{-20,11,-4,13,-5,-2}中，最大子序列为{11,-4,13}，其和为20。

基本思想：
1.划分
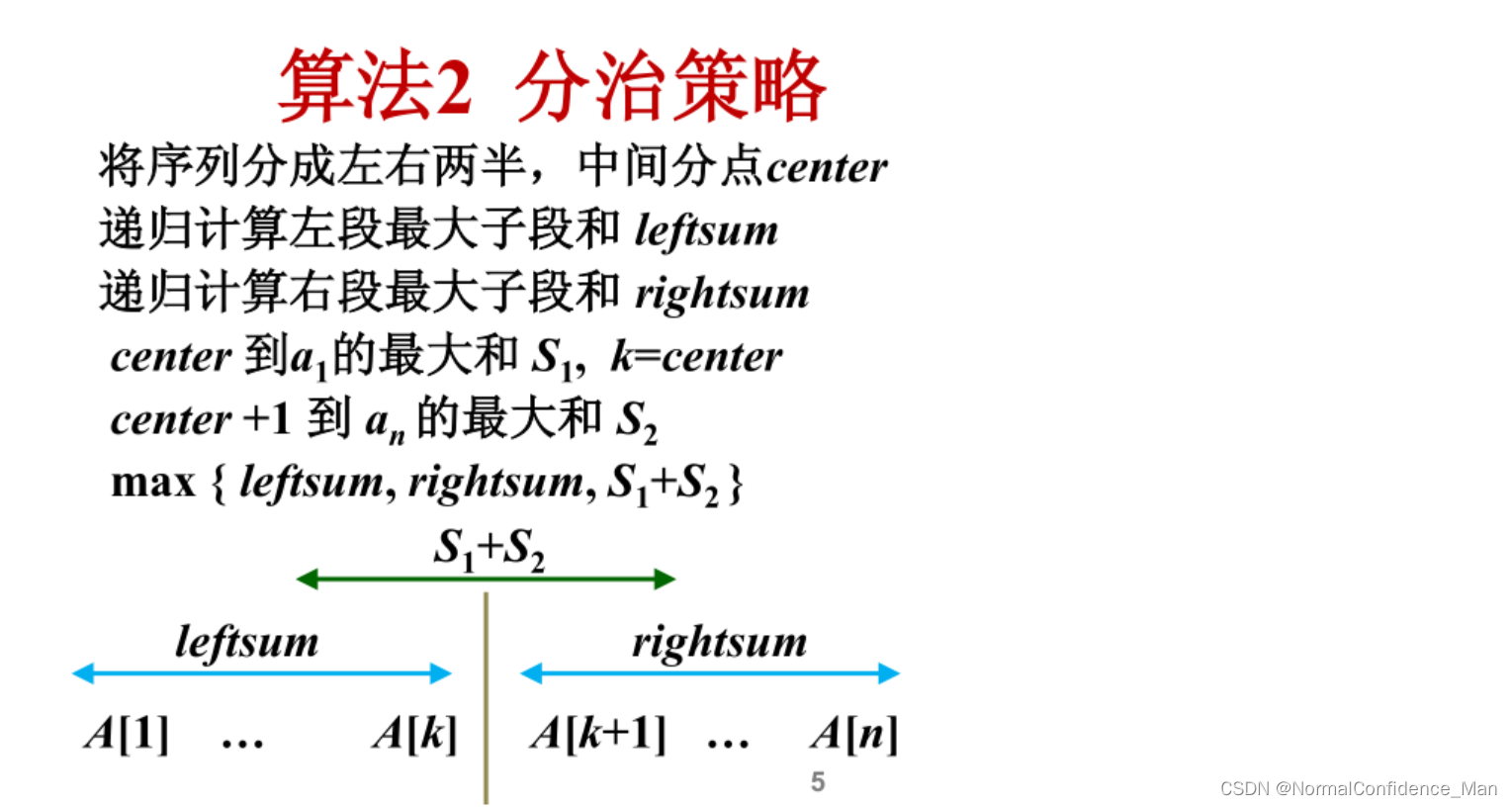
按照平衡子问题的原则，将序列{a1,a2,a3,…,an}等分为两个长度相同的子序列{a1,a2,…,a_n/2}和{a_n/2+1,a_n/2+2,…,a_n}，则会出现以下三种情况。

1. a1,a2,a3,…,an的最大子段和={a1,a2,…,a_n/2}的最大子段和,也就是原序列的最大字段和等于左半序列的最大子段和
2. a1,a2,a3,…,an的最大子段和={a_n/2+1,a_n/2+2,…,a_n}的最大子段和，也就是原序列的最大字段和等于右半序列的最大子段和
3. a1,a2,a3,…,an的最大子段和一部分位于左半序列，一部分位于右半序列

2.求解子问题
对于第一、第二种情况，可以使用递归求解，对于第三种情况，则需要分别计算从第i个到第n/2的最大字段和S1和从第n/2+1个到第j个最大子段和S2，此时两个最大子段和之和就是情况3的最大子段和。

合并：比较3中情况下的最大字段和，选出三者中最大的作为问题的解。

算法分析：
时间复杂度为O(nlog₂n)

棋盘覆盖问题

问题：
在一个2^k*2^k个方格组成的棋盘中，恰好有一个方格和其他方格不同，该方格被称为特殊方格。显然，特殊方格可能出现的位置有4^k种，因此有4^k种棋盘。棋盘覆盖问题要求是用4中不同的L形骨牌覆盖给定棋盘上除了特殊方块以外的所有方格，并且任何两个L形骨牌不可以重叠。

基本思想：
如何采用分治法解决该问题呢？关键在于如何划分棋盘，划分后的子棋盘的大小是相同的，并且每一个都包含一个特殊方格，从而将原问题分解为较小的的棋盘覆盖问题。比如一个4x4的棋盘可以将其划分为4个2x2的棋盘。但是这样的话就只会有一个子棋盘中含有特殊方块了。为了将这三个没有特殊方格的子棋盘转化为特殊棋盘，将各个子问题的情况统一起来，可以用一个L形骨牌覆盖这三个子棋盘的汇合处，如下图所示。

递归地使用这种策略，直到将棋盘划分为1x1的子棋盘，此时该子棋盘中唯一一个方块就是特殊方块。然后进行合并，将4个1x1的方块合成一个2x2的方块，此时该2x2的方块刚好可以塞得下一个L形骨牌，然后剩余的一个方块就是特殊方块。以此类推，继续合并直到合并成原来的样子。

几何问题中的分治法

最近点对问题

该问题在之前的穷举法中有所介绍。在一个二维平面上有n个点构成的集合S，需要找出这n个点中距离最近的一对点，严格来讲，最近点对可能不唯一，但是只要找出其中之一即可

思想：
最近点对问题的分治法解法策略如下：
1.划分：将集合S划分为两个子集S1和S2，根据平衡子问题原则，每个子集中大约有n/2个点，假设集合S中最近点对为pi和pj，那么会出现如下三种情况：
(1)pi和pj都在S1中
(2)pi和pj都在S2中
(3)pi在S1中，pj在S2中

2.求解子问题
对于情况1和2来说，可以使用递归求解，但是对于情况3的处理就比较复杂了。在划分子集的时候，一般选取垂直线x=m作为分割线，设S1中的最近距离为d1，S2中的最近距离为d2，设d=min{d1, d2}，假设S之间的最近对{p,q}距离小于d，则p和q肯定分别属于S1和S2，此时p和q肯定位于以x=m为中心，宽度为2d的垂直带p1和p2中，如下图：

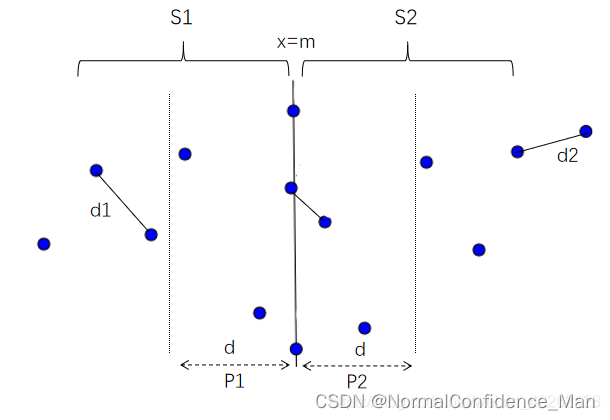
假设点p(x,y)是集合P1和P2中y坐标最小的点，则p即可能在P1中也可能在P2中。现在需要找出的是和点p的距离小于d的点，显然，这些点肯定位于[y, y+d]之间，如下图所示，根据鸽笼定理，这样的点不会超过8个，因为P1和P2之间各个点相距距离至少为d。

所以我们可以按照y坐标升序排序P1和P2之间的点，然后依次处理P1和P2之间的点p(x,y)，选出位于[y,y+d]的候选点，计算他们之间的距离，然后选出他们之间的最小距离。

3.比较在划分节点三种情况下的最近点对，取三者之中距离较小者为问题的解。

3.算法开销
算法的时间复杂度为O(nlong₂n)