ZO-signSGD

论文信息

题目：SIGNSGD VIA ZEROTH-ORDER ORACLE

作者：Sijia Liu, Pin-Yu Chen, Xiangyi Chen, Mingyi Hong

会议： ICLR (International Conference on Learning Representations)

单位：MIT-IBM Watson AI Lab, IBM Research

论文动机

• 黑盒问题由于得到不模型具体信息，仅能获取模型的查询结果，因此一直限制着对抗样本的设计；
• Zeroth order optimization能够解决梯度很难获得或不可得情况，一直倍受关注；
• 而利用攻击损失的梯度估计的符号信息可以生成高性能的对抗样本，受到这个的启发，考虑能不能利用Zeroth order optimization去估计梯度符号，在利用梯度符号估计去生成高性能对抗样本；
• 在之前论文，在一阶设定中，显示了signSGD不仅降低了梯度传递的每次迭代成本，而且可以产生比SGD更快的经验收敛速度，signSGD在足够大的小批量大小的条件下达到$O(1/\surd T)$收敛速率；
• 考虑到signSGD的优势，将ZO扩展运用其中是否也能得到类似的收敛速率表达式

前人方法

• Bernstein等人¹证明了signSGD不仅降低了梯度传递的每次迭代成本，而且可以产生比SGD更快的经验收敛速度；
• 在足够大的小批量大小的情况下，signSGD达到$O(1/\surd T)$收敛速度，其中T表示迭代的总数。Balles＆Hennig²中的工作通过限制性凸分析在signSGD和Adam之间建立了联系；
• signSGD尚未正式定义，用于生成白盒对抗示例的快速梯度符号方法（Goodfellow等³，2015）实际上遵循signSGD的算法协议；
• 强大的深度神经网络对抗训练证明了signSGD的有效性（Madry等⁴，2018）。

本文方法

问题描述
1.满足signSGD的对抗样本：

• 问题定义：
  $x_0$,$t_0$为真实输入样本以及标签，$x^{\prime }=x_0+\delta$表示设计的对抗样本，$f(x,t)$是学习模型的训练损失
• 目标：最小化$\delta$使得$f(x_{\prime },t_0)$最大化
• 求解：
  $$f\left({\mathbf{x}}^{\prime },t_0\right)\approx f\left({\mathbf{x}}_0,t_0\right)+⟨{\nabla }_{\mathbf{x}}f\left({\mathbf{x}}_0,t_0\right),\mathbf{\delta }⟩$$
  限制扰动$\delta$在$l_{\infty }$小半径$ϵ$球上
  $$\delta =ϵsign(⟨{\nabla }_{\mathbf{x}}f\left({\mathbf{x}}_0,t_0\right))$$
  因此，最大化$f(x^{\prime },t_0)$变成了最大化$\delta$(因为$⟨{\nabla }_{\mathbf{x}}f\left({\mathbf{x}}_0,t_0\right),\mathbf{\delta }⟩=ϵ|⟨{\nabla }_{\mathbf{x}}f\left({\mathbf{x}}_0,t_0\right)|$)
• 从而，对抗样本更新规则为
  $${\mathbf{x}}^{\prime }={\mathbf{x}}_0-ϵ\mathrm{sign}\left(-{\nabla }_{\mathbf{x}}f\left({\mathbf{x}}_0,t_0\right)\right)$$

2.ZO方法估计梯度：这里采用forward difference
$$\text{ GradEstimate }(\mathbf{x})=\frac{1}{bq}\sum _{i\in {\mathcal{I}}_k}\sum _{j=1}^q\hat{\nabla }{f}_i\left(\mathbf{x};{\mathbf{u}}_{i,j}\right),\hat{\nabla }{f}_i\left(\mathbf{x};{\mathbf{u}}_{i,j}\right):=\frac{d\left[f_i\left(\mathbf{x}+\mu {\mathbf{u}}_{i,j}\right)-f_i(\mathbf{x})\right]}{\mu }{\mathbf{u}}_{i,j}$$
${\mathcal{I}}_k$是小批量的大小$|{\mathcal{I}}_k|=b$，${\mathbf{u}}_{i,j}$是单位球上的均匀分布（也可以使用高斯分布，但是球均匀分布在实际中由于是有界可能更有用），$\mu$是光滑参数

上式为有偏估计，而对于光滑参数$\mu$的无偏估计
$$f_{\mu }(\mathbf{x})={\mathbb{E}}_{\mathbf{v}}[f(\mathbf{x}+\mu \mathbf{v})]=\frac{1}{n}\sum _{i=1}^n{\mathbb{E}}_{\mathbf{v}}\left[f_i(\mathbf{x}+\mu \mathbf{v})\right]=\frac{1}{n}\sum _{i=1}^n{f}_{i,\mu }(\mathbf{x})$$
$f_{i,\mu }$是$f_i$的随机光滑形式，$\mathbf{v}$则是unit Euclidean ball上的均匀分布，虽然，在ZO梯度估计和f的真实梯度之间存在一个间隙，但是如稍后将看到的那样，可以通过平滑函数$f_{\mu }$测量这种间隙

3.ZO-signSGD动机

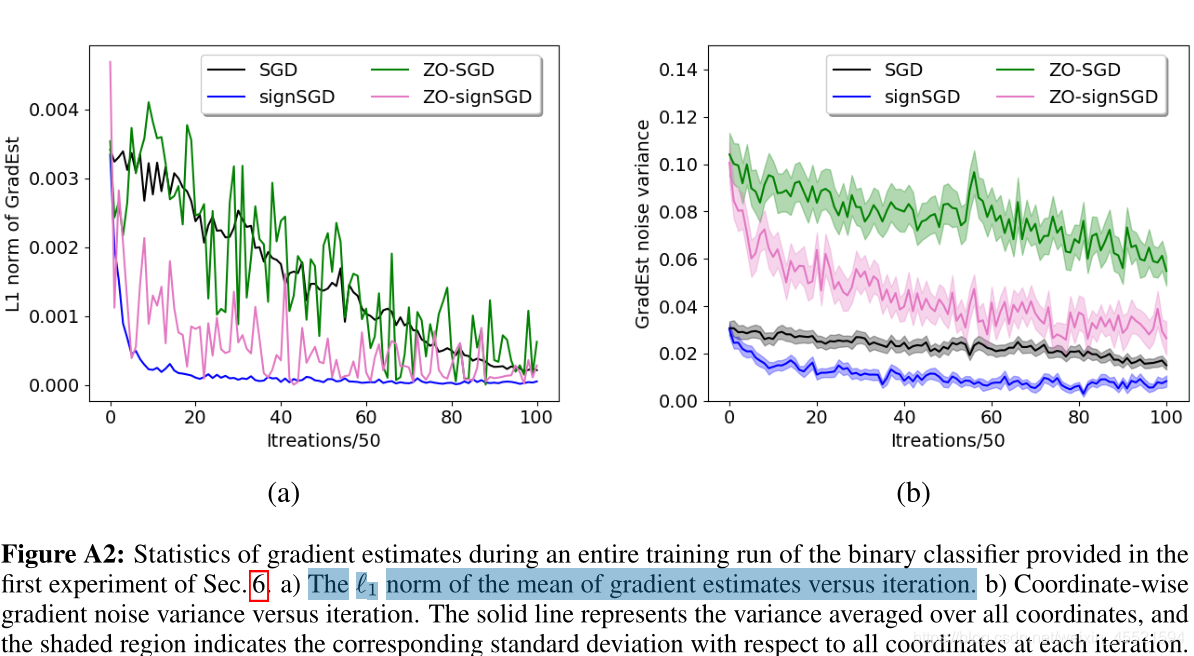
• ZO梯度估计是真实梯度的偏差近似值，因此，与（一阶）随机梯度相比，噪声方差可能更大
  
  实线表示随机初始化的10个独立试验的平均损失，阴影区域表示随机试验的结果标准差
• 而符号(sign)运算可以减轻大方差（坐标）梯度噪声的负面影响，因此，采用梯度估计的符号可能会缩小极度嘈杂的分量
  
  4.ZO-signSGD与signSGD三个区别
• ZO-signSGD对小批量采样的选择有较温和的假设。（Bernstein et al¹）中的signSGD达到$O(1/\surd T)$收敛速度，而且条件是最小批量大小足够大，$b=O(T)$，但是，仅当从$[n]$中随机选择微型批次样本进行替换时，此条件才成立，这在$n\le T$时是不常见的。这里[n]表示整数集 { 1 , 2 , ⋯ ， n } \{1,2,\cdots ，n\} {1,2,⋯，n}。当$b=n$时，signSGD无法覆盖signGD，因为即使b = n，替换采样也会导致${\mathcal{I}}_k!=[n]$。在提出的ZO-signSGD算法中，我们将放宽对小批量采样的假设
• 在ZO-signSGD中，ZO梯度估算器和正负号算子都会对真实梯度产生近似误差,尽管可以借助随机平滑函数来获取ZO梯度估计的统计特性，但是使用无替代的小批量采样会带来额外的困难来限制ZO梯度估计的方差，因为没有小批量样本不再独立，此外，基于符号的下降算法会评估1-范数几何中的收敛误差，从而导致与基于2-范数的梯度方差不匹配。除了将梯度范数从 1转换为2之外，还采用概率收敛方法来约束ZO-signSGD的最终收敛误差
• 除了标准的ZO梯度估算器，我们还将介绍ZOsignSGD的多个变体，以进行集中式或分布式优化

本文方法

• 证明具体见paper

方法优势与缺陷

• 提出ZO-signSGD可能不会收敛到非常高精度的解决方案，但是可以收敛到足以以非常快的速度进行黑箱攻击的中等精度

实验结果

1.二分类

• 优化目标
  $$\underset{\mathbf{x}\in {\mathbb{R}}^d}{\min }\frac{1}{n}\sum _{i=1}^n{\left(y_i-1/\left(1+e^{-{\mathbf{a}}_i^T\mathbf{x}}\right)\right)}^2$$
  { a i } \left\{\mathbf{a}_{i}\right\} {ai​}来自 $\mathcal{N}(0,\mathbf{I}),$ 而且获得label，如果$1/\left(1+e^{-{\mathbf{a}}_i^T\mathbf{x}}\right)>0.5$ 则$y_i=1$ 否则为0，实验结果如下。
  
  
• 我们从图1（a）和（b）观察到，ZO-signSGD优于其他ZO算法，并且一旦获得一阶信息，signSGD将产生最佳的收敛性能
• 在图1（c）和（d）中，我们观察到ZO算法的收敛性能随着b和q的增加而提高。特别是，b = q = 30时的ZO-signSGD和ZO-M-signSGD接近signSGD提供的最佳结果。在图1（e）和（f）中，随着问题大小d的增加，所有算法的收敛性都会降低。但是，ZO-signSGD和ZO-M-signSGD的收敛速度比ZO-SGD和ZO-SCD快
  
  在图2中，我们证明了ZO-signSGD不同变体对于b∈{40,400}的收敛轨迹。为了公平地比较ZOsignSGD和ZO-D-signSGD，让M = 40的每个代理使用大小为b / M的小批量。如我们所见，ZO-signSGD的性能优于ZO-M-signSGD和ZO-D-signSGD。随着小批量的增加，收敛性得到改善。

2.产生对抗样本

• 优化目标为（为非目标优化）

$$\underset{\mathbf{w}\in {\mathbb{R}}^d}{\mathrm{minimize}}c\cdot \max \left\{\log F_{t_0}(\tanh (\mathbf{w})/2)-\underset{i\ne t\in \mathrm{lo}}{\max }\log F_j(\tanh (\mathbf{w})/2),0\right\}+{\Vert \tanh (\mathbf{w})/2-{\mathbf{x}}_0\Vert }_2^2$$

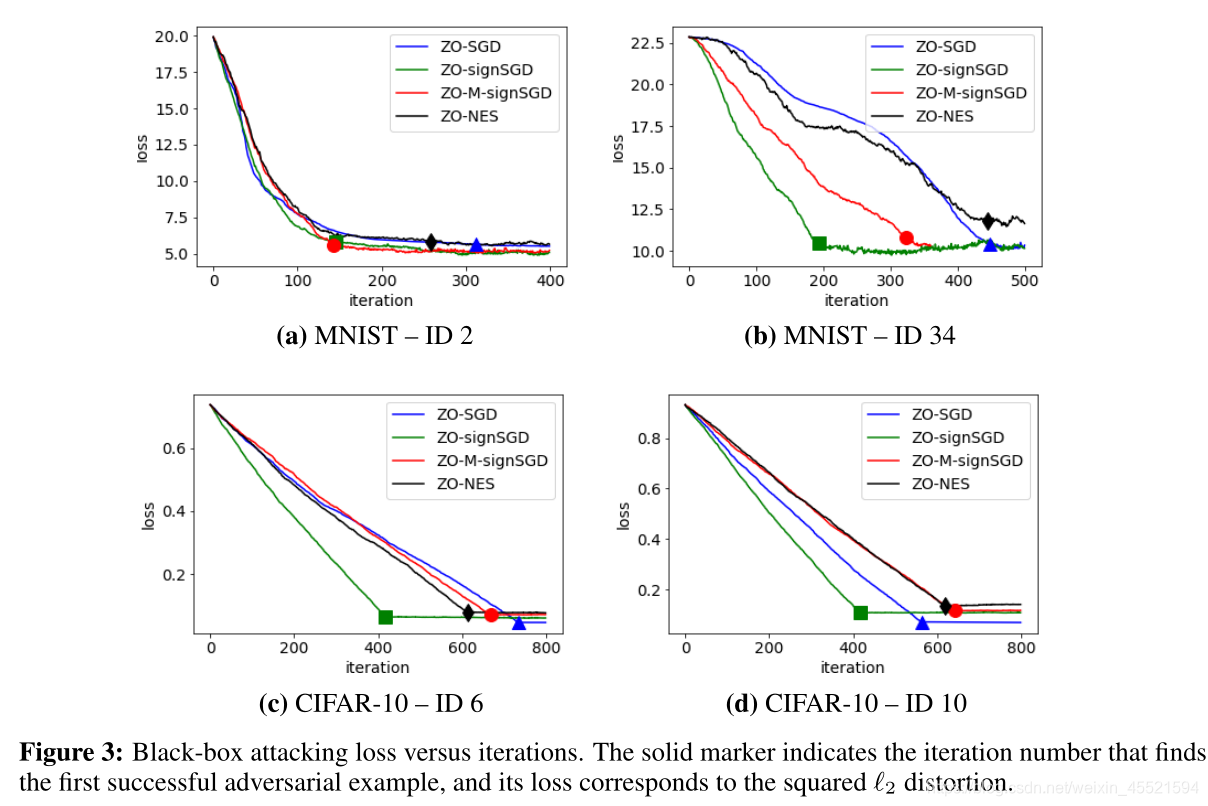
对于MNIST，要找到第一个成功的对抗示例，所有受攻击图像的平均迭代是ZO-SGD为184，ZO-signSGD为103，ZO-M-signSGD为151，ZO-NES为227。 ZO-SGD的平均平均值’2失真为2.345，ZO-signSGD的平均值为2.381，ZO-MsignSGD的平均值为2.418，ZO-NES的平均值为2.488

对于CIFAR-10，要找到第一个成功的对抗示例，所有受攻击图像的平均迭代是ZO-SGD为302，ZO-signSGD为250，ZO-M-signSGD为389，ZO-NES为363。 ZO-SGD的平均平均值’2失真为0.177，ZO-signSGD的平均值为0.208，ZO-M-signSGD的平均值为0.219，ZO-NES的平均值为0.235

• 如我们所见，ZO-signSGD和ZO-M-signSGD可以比ZO-SGD减少约54％的迭代（约少600个模型查询），从而找到第一个成功的对抗示例
• 给定第一个成功的对抗示例，我们观察到ZO-signSGD产生的l2失真比ZO-SGD略高，正如论文中所证明提出ZO-signSGD可能不会收敛到非常高精度的解决方案，但是可以收敛到足以以非常快的速度进行黑箱攻击的中等精度
• 在查询效率（由实现首次成功攻击的迭代次数决定）或攻击失真方面，ZO-NES都不如ZO-signSGD有效。因此，与ZO-NES相比，ZO-signSGD提供了一种可证明且有效的黑盒对抗攻击方法

总结：

• 严格证明了ZO-signSGD及其变体在mild条件下的$O（\surd d/\surd T）$收敛速度
• 与signSGD相比，ZO-signSGD的收敛速度较慢（与问题大小d成正比），但是它具有无梯度的优点
• 与其他ZO算法相比，我们证实了ZO-signSGD在合成和实词数据集（synthetic and real-word datasets）上均具有出色的性能，特别是将其应用于黑盒对抗攻击中
• 提出ZO-signSGD可能不会收敛到非常高精度的解决方案，但是可以收敛到足以以非常快的速度进行黑箱攻击的中等精度

下步工作

• 希望将分析推广到非平滑和非凸约束优化问题。

参考文献

---

1. Bernstein, Y .-X. Wang, K. Azizzadenesheli, and A. Anandkumar. signsgd: compressed optimisation for non-convex problems. arXiv preprint arXiv:1802.04434, 2018 ↩︎ ↩︎

2. Balles and P . Hennig. Dissecting adam: The sign, magnitude and variance of stochastic gradients. arXiv preprint arXiv:1705.07774, 2017 ↩︎

3. Alexey Kurakin, Ian J. Goodfellow, and Samy Bengio. Adversarial machine learning at scale. 2017 ICLR, arXiv
   preprint arXiv:1611.01236, 2017. URL http://arxiv.org/abs/1611.01236. ↩︎

4. Madry, A. Makelov, L. Schmidt, D. Tsipras, and A. Vladu. Towards deep learning models resistant to
   adversarial attacks. ICLR, 2018 ↩︎