目录
1.Traveling Salesman Problem(TSP)
2.Capacitated Vehicle Routing Problem (CVRP)
2.1.1 two-Index Vehicle Flow Formulation
2.1.2 three-Index Vehicle Flow Formulation
3.Vehicle routing problems with time windows (VRPTW)
4.Pickup and delivery problem with time window(PDPTW)
- 旅行商问题TSP:模型✅,代码✅
- 容量约束车辆路径规划问题:模型✅,代码✅
- 取送货车辆路径规划问题:模型✅,代码✅
- 时间窗约束车辆路径规划问题:模型✅,代码✅
Gurobi求解代码https://github.com/bujibujibiuwang/Routing-Problem
1.Traveling Salesman Problem(TSP)
1.1 TSP数学模型
参考:维基百科TSP
给定一些城市和城市之间的距离,找到最短路径,经过每个城市最后返回起点,组合优化问题中属于NP-hard难度。对于TSP问题有两类混合整数规划模型:Miller–Tucker–Zemlin (MTZ)形式和Dantzig–Fulkerson–Johnson (DFJ)形式,DFJ模型更好,但是在某些特定条件下,MTZ模型仍然有用。两类模型有一些通用的符号。


上述模型不能保证解中不出现子回路,我们只需要得到一个经过所有点的回路,有以下两种方式消除子回路。
- Miller–Tucker–Zemlin formulation(MTZ)

- Dantzig–Fulkerson–Johnson formulation(DFJ)

两种形式的完整数学模型如下:

1.2 Gurobi测试
官方资料Traveling Salesman Problem
用求解器DFJ模型,比较难处理的是子圈消除约束,指数量级的约束,因此使用回调函数来查找违反的子圈约束并将它们作为惰性约束添加到模型中。子圈消除代码如下:
# 子圈消除约束:callback + lazy constraints
def sub_tour_eliminate(model, where):
# 如果当前优化状态为找到新的MIP解
if where == GRB.Callback.MIPSOL:
# 获取当前解
values = model.cbGetSolution(model._vars)
selected = gp.tuplelist((i, j) for i, j in model._vars.keys() if values[i, j] > 0.5)
# 找到最小的圈
cycle = get_sub_tour(selected)
# 如果最小的圈长度不等于节点数,表明是子圈,将该圈的子圈消除约束添加到模型中
if len(cycle) < number:
model.cbLazy(gp.quicksum(model._vars[i, j] for i, j in combinations(cycle, 2)) <= len(cycle) - 1)
# 找到最小的子圈,用于添加lazy constraints
def get_sub_tour(edges):
unvisited = [p.index for p in points]
cycle = edges[:]
while unvisited:
current_cycle = []
neighbors = unvisited
while neighbors:
current = neighbors[0]
current_cycle.append(current)
unvisited.remove(current)
neighbors = [j for i, j in edges.select(current, '*') if j in unvisited]
if len(current_cycle) < len(cycle):
cycle = current_cycle
return cycleberlin52 instance求解结果如下,能找到最优解7544
Optimal solution found (tolerance 1.00e-04)
Best objective 7.544365901904e+03, best bound 7.544365901904e+03, gap 0.0000%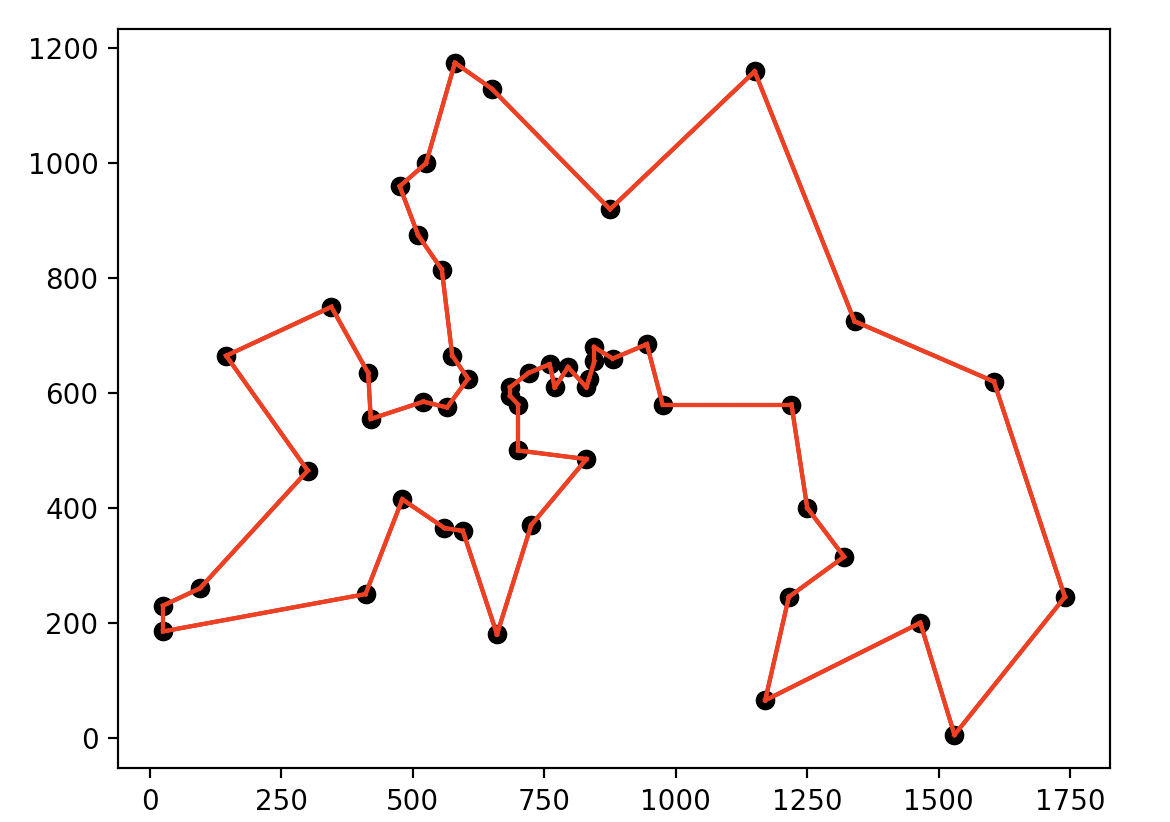
2.Capacitated Vehicle Routing Problem (CVRP)
参考:维基百科VRP
VRP问题描述:给定一组客户点、车辆容量、车辆数量、起始点和终点,目标是找到使得所有客户点都被访问一次的最短路径方案,这是TSP问题的扩展。
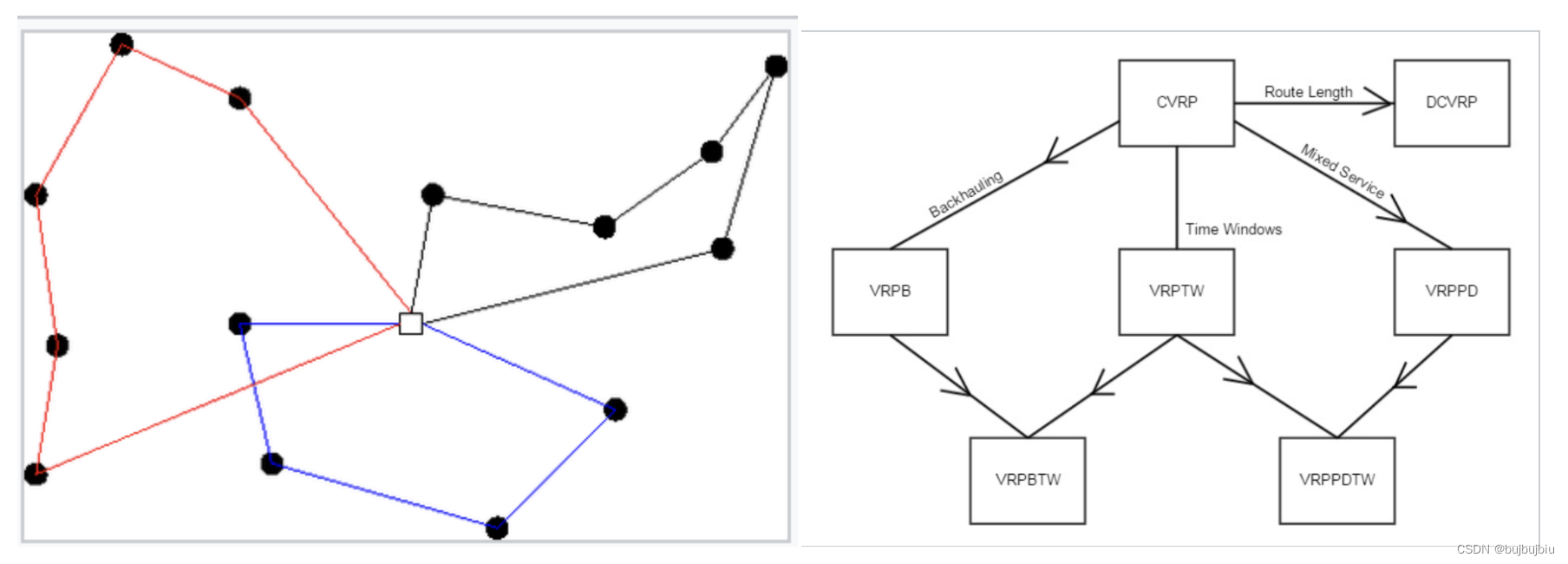
VRP变种:
- Vehicle Routing Problem with Pickup and Delivery (VRPPD):具有提货和交付的车辆路径规划问题。有一组车辆需要从仓库或起始点出发,分别访问一系列提货地点以收集货物,然后将货物交付到相应的交付地点,最终返回仓库或结束点。问题的目标通常是最小化总行驶距离、时间或成本,或者在满足一定的约束条件下,找到一组最佳的路线方案
- Capacitated Vehicle Routing Problem (CVRP):容量限制车辆路径规划问题。在CVRP中,每辆车辆都有一个限定的最大携带容量
- Vehicle Routing Problem with Time Windows (VRPTW):带有时间窗口的车辆路径规划问题。在VRPTW中必须在每个配送地点的时间窗口内完成配送。时间窗口表示了在一定的时间范围内必须到达每个客户或配送地点,以满足客户的需求
2.1 CVRP数学模型
CVPR有多种建模方式,下面介绍了two-Index Vehicle Flow Formulation 和 three-Index Vehicle Flow Formulatiom以及基于MTZ的CVRP模型,使用Gurobi测试了第3种模型。
2.1.1 two-Index Vehicle Flow Formulation


该模型中变量数为,
个等式,
个不等式,共
个约束
2.1.2 three-Index Vehicle Flow Formulation


2.1.3 MTZ+CVRP模型
VRP问题相比TSP,不同在于中心点可以多次访问,因此只需要在模型中把起点约束修改,再增加容量约束,使用MTZ或者DFJ方法消除子圈即可。使用MTZ方法,增加一个虚拟变量表示流经该点的流量,即能控制顺序也能确保车辆容量约束。
给定所有点的位置,客户点的需求,设定可用车辆数,所有车都有相同的容量限制,要求安排车辆运输路线实现总距离最小。


2.2 Gurobi测试
在VRP数据集上测试,数据集给定了每个点的位置和需求,以及可使用车辆数和车载最大容量,下面是MTZ+CVRP模型的部分代码:
"""
(2)决策变量和目标函数
"""
model = gp.Model('VRP')
select = model.addVars(edges, vtype=GRB.BINARY, name='select')
flow = model.addVars(customers, vtype=GRB.CONTINUOUS, name='flow')
model.setObjective(select.prod(distance), GRB.MINIMIZE)
"""
(3)约束条件
"""
# 每个客户点一条出边
model.addConstrs(gp.quicksum(select[i, j] for j in points if j != i) == 1 for i in customers)
# 每个客户点一条入边
model.addConstrs(gp.quicksum(select[i, j] for i in points if i != j) == 1 for j in customers)
# 流量顺序约束
model.addConstrs((select[i, j] == 1) >> (flow[i] + points_list[j].demand == flow[j])
for i, j in edges if i != 0 and j != 0)
# 流量大小约束
model.addConstrs(points_list[i].demand <= flow[i] for i in customers)
model.addConstrs(flow[i] <= vehicle_capacity for i in customers)
# 车辆数量约束
model.addConstr(gp.quicksum(select[0, j] for j in customers) <= vehicle_count)
model.addConstr(gp.quicksum(select[i, 0] for i in customers) <= vehicle_count)在16个点,3辆车,90容量的测试样例下求解最优解为278
Optimal solution found (tolerance 1.00e-04)
Best objective 2.787262997478e+02, best bound 2.787262997478e+02, gap 0.0000%
3.Vehicle routing problems with time windows (VRPTW)
3.1 VRPTW模型
VRPTW问题和CVRP相比,还要求车辆到达每个客户点的时间要在规定范围内,因此在CVRP模型基础上增加时间窗约束即可。

决策变量有三个:(1) 代表路径选择的0-1变量(2)消除子圈约束的流量(3)限制时间窗的开始时间

约束条件和CVRP模型相同,只是增加了时间窗约束

3.2 Solomon数据集测试
使用Solomon基准数据集验证模型,时间窗约束代码如下:
model.addConstrs(start[i] + int(distance[(i, j)]) + time[i] - BigM * (1 - select[i, j]) <= start[j] for i, j in edges if j != 0)
model.addConstrs(start[i] >= points_list[i].ready for i in points)
model.addConstrs(start[i] <= points_list[i].due for i in points)其中C101样例,100个点的求解结果最优值为828,与官方最优解828.94一致
Optimal solution found (tolerance 1.00e-04)
Best objective 8.289368669428e+02, best bound 8.289368669428e+02, gap 0.0000%
route0:[0, 5, 3, 7, 8, 10, 11, 9, 6, 4, 2, 1, 75, 0]
route1:[0, 13, 17, 18, 19, 15, 16, 14, 12, 0]
route2:[0, 20, 24, 25, 27, 29, 30, 28, 26, 23, 22, 21, 0]
route3:[0, 32, 33, 31, 35, 37, 38, 39, 36, 34, 0]
route4:[0, 43, 42, 41, 40, 44, 46, 45, 48, 51, 50, 52, 49, 47, 0]
route5:[0, 57, 55, 54, 53, 56, 58, 60, 59, 0]
route6:[0, 67, 65, 63, 62, 74, 72, 61, 64, 68, 66, 69, 0]
route7:[0, 81, 78, 76, 71, 70, 73, 77, 79, 80, 0]
route8:[0, 90, 87, 86, 83, 82, 84, 85, 88, 89, 91, 0]
route9:[0, 98, 96, 95, 94, 92, 93, 97, 100, 99, 0]
4.Pickup and delivery problem with time window(PDPTW)
4.1 PDPTW模型
带时间窗的取送货路径规划问题(pickup and delivery problem with time window,PDPTW)是路径规划问题的一个重要子类,在供应链领域比较常见,例如某物流企业需要指定交易未来某段时间内车辆的运输调度计划,在满足货物运输要求前提下最小化运输成本。下面基于Gurobi官方资源进行PDPTW案例分析,数据有3张表:地点信息表,车辆信息表,订单信息表。
(1)地点信息表:所有订单可能取送货的地点,包括停靠点ID,纬度和经度

(2)车辆信息表:可用车辆的信息,包括每辆车的起始和结束点,服务时间,时间和距离限制,运输速度,单位成本,匹配关系等

(3)订单信息表:要取送货的订单集合,包括每个订单的取送货时间窗,服务时间,取送货地点,匹配关系等

对于数学模型,首先要明确想要模型求解出什么信息?有一些是目标的决策变量,有一些是辅助的决策变量。在该问题中,我们想知道每辆车负责运输那些订单,这些订单的运输线路是那样的?那么最直观的建模思路是:(1)用一个0-1变量来表示是否运输该订单(2)用另一个0-1变量来表示在选中的订单中的运输边。但是(2)实际上已经包括(1),因为选中了某条运输边,就代表这个运输边包含的订单也被选中;并且在Gurobi建模中决策变量不能作为索引,即不能通过(1)的信息来约束(2)。
换成另一个建模思路:对每辆车,获取匹配关系对应的订单的取送货候选点集合,该车辆只会经过该候选点集合组成的边。如果候选点集合是真实的地点,那么会出现一个真实地点比如L1会有多个订单都经过,即L1在多辆车的候选点集合中,决策变量只会体现出是否经过L1,但是不清楚经过L1取哪个订单,因此候选点集合不能是真实的地点,而是虚拟的地点,即假设每个订单的取送货点都是独立的,但是计算距离时采用虚拟点对应真实点的经纬度。
对每辆车:虚拟点包括起始虚拟点,结束虚拟点,取送货虚拟点。


4.2 Gurobi测试
以下代码建模部分用pulp库实现,可支持调用多种求解器(cplex, gurobi等)进行求解,部分代码实现如下:
- 保证先取后送
def add_seq_cons(self):
# (13) 保证货物先取后送
for key in self.a_vars.keys():
k, i = key[0], key[1]
veh_obj = self.system.vehicle_obj_dict[k]
if i % 2 != 0 and i != 0 and i != (self.system.dummy_node_count + 1):
node_pick, node_del = i, i + 1
order_id, loca_i_name, _ = self.system.dummy_node_dict[node_pick]
loca_j_name = self.system.dummy_node_dict[node_del][1]
order_obj = self.system.order_obj_dict[order_id]
trans_time = round((self.system.dist_matrix[(loca_i_name, loca_j_name)] / veh_obj.speed) * 3600)
lhs = self.a_vars[(k, node_pick)] + self.w_vars[(k, node_pick)] + order_obj.pick_service + trans_time
self.model += (lhs <= self.a_vars[(k, node_del)], f'{k}_{i}_{i + 1}_seq_cons')
- 添加负载平衡约束
def add_load_cons(self):
# (5) 负载平衡约束:如果车辆k经过边(i,j),那么到达i的负载量+节点j的负载量=到达j的负载量
for key in self.x_vars.keys():
k, i, j = key[0], key[1], key[2]
veh_obj = self.system.vehicle_obj_dict[k]
big_M = 2 * veh_obj.max_load
lhs = self.q_vars[(k, j)]
if i == 0:
rhs = self.q_vars[(k, i)] + (self.x_vars[key] - 1) * big_M
else:
load_i = self.system.dummy_node_dict[i][2]
rhs = self.q_vars[(k, i)] + load_i + (self.x_vars[key] - 1) * big_M
# 为了将约束线性化,引入bigM,必须要用不等式,导致该约束限制不了环路的出现
self.model += (lhs >= rhs, f'{key}_load_balance_cons')1000s后找到gap为45%的最优解,与官方给出代码运行效果基本一致,求解的调度计划也一致
Explored 664725 nodes (14855641 simplex iterations) in 600.01 seconds (680.73 work units)
Thread count was 8 (of 8 available processors)
Solution count 10: 846.682 846.682 846.682 ... 876.259
Time limit reached
Best objective 8.466817613171e+02, best bound 4.627762720459e+02, gap 45.3424%


PDPTW在如此小规模问题下都需要较长求解时间,求解时间是比较长的,在实际应用中,车辆调度次数比较频繁,约束更复杂,因此往往采用启发式算法来实现,能比较快找到一个次优解。
























 154
154

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








