升余弦滤波器与无码间串扰（一）

目录

升余弦滤波器与无码间串扰（一）
升余弦滤波器与无码间串扰（二）
升余弦滤波器的FPGA实现

---

ISI

基带系统中，把发送滤波器、信道、接收滤波器的总特性看作h(t)，基带的每个码元经过h(t)后码元波形会进行畸变、展宽，波形会出现拖尾，即本码元的波形不会仅局限在本码元的TB上，而是蔓延到其他码元的抽样时刻上，如果在某个码元抽样时刻上累积的ISI很大，则会影响对该码元的判决。

无码间串扰的基带传输特性

• 基带传输系统模型
  

---

• 基带序列
  

---

• 接收滤波器输出
  

---

• 在t=k*TB+t0对第k个码元采样，t0是信道和接收滤波器所造成的延时
  

---

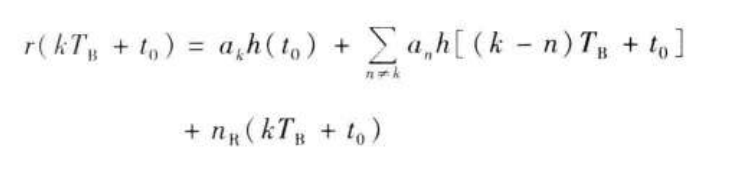
• 消除ISI的条件（先不考虑噪声）
  
  由于an是随机变量，为了实现上求和式等于0，考虑每个码元的波形在本码元的抽样时刻上有最大值，在其他码元的抽样时刻上为0（假设t0=0）。
• 无ISI的时域条件
  
• 无ISI的频域条件
  

---

• 理想低通特性
  满足无ISI的H（Ω）有很多种，有一种极限情况是理想低通特性
  
  用带宽B=1/(2TB)的理想低通特性的基带传输系统，来传输RB=1/TB的基带信号，则在抽样时刻上不存在码间串扰
  理想低通传输特性是基带系统实现无码间串扰的最小带宽，如果要传输的基带信号的波特率是RB，则最小要用1/2RB的带宽来传输，此时对应基带系统能提供的最高频带利用率2Baud/Hz

• 奈奎斯特带宽 fN=1/(2TB)

• 奈奎斯特速率（无ISI的最高传输速率）：2fN Baud

---

• 余弦滚降特性

理想低通特性无法实现而且h(t)尾部衰减慢，振幅大，对定时要求严格，所以我们用余弦滚降特性的传输系统

用滚降特性代替原来陡峭的边沿。
传输系统带宽B=（1+a）fN

带通系统中的升余弦滤波

以上分析的都是基带传输系统满足升余弦特性可以实现抽样时刻上无ISI，那么带通系统中的升余弦滤波器是否有相似的特性呢？

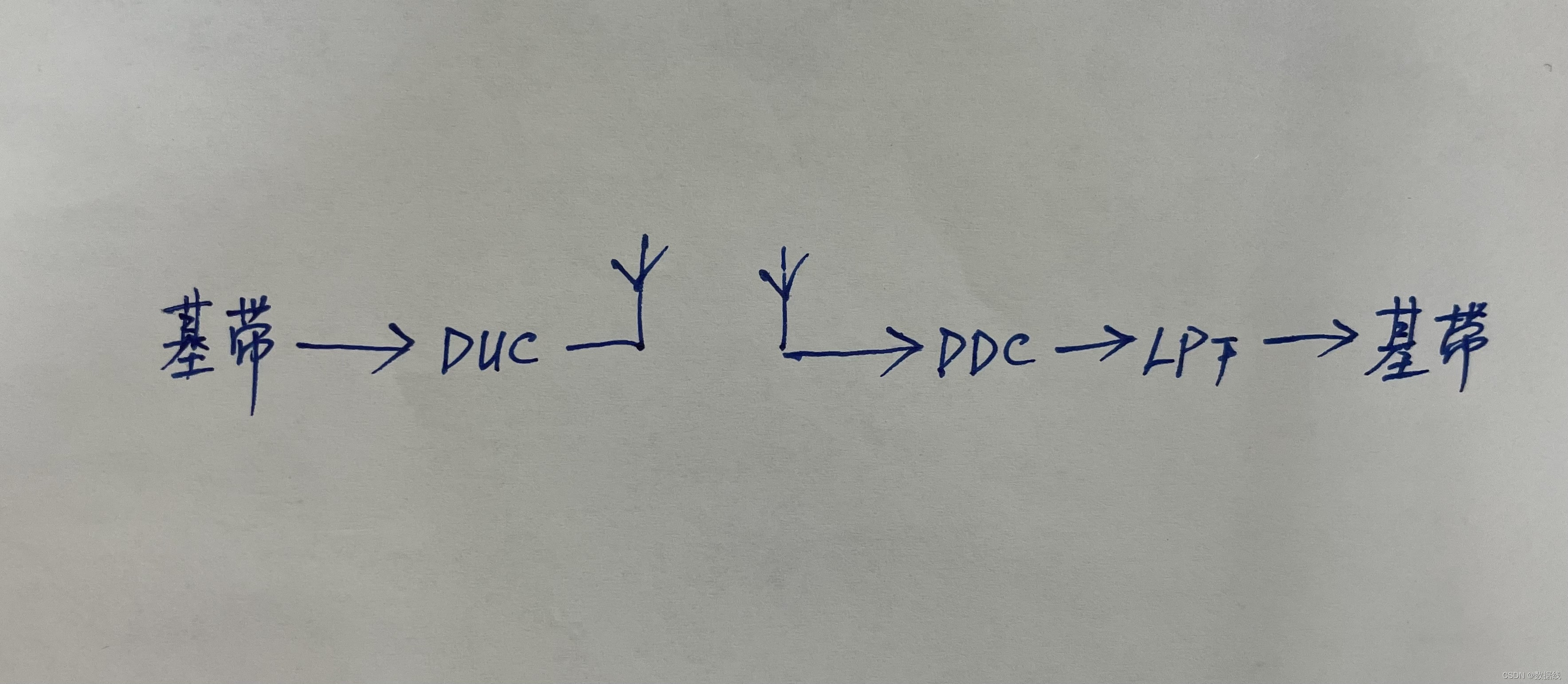
根据带通系统的框图，上变频和相干解调的部分可以相互抵消，如果发送的基带信号满足在抽样时刻上无ISI，那么解调端，相干解调后得到的基带信号在抽样时刻上也无ISI。所以，在上变频之前会进行升余弦滤波，使基带信号在抽样时刻上无ISI。