1.模型架构
- Transformer是深度学习领域中的一个重要模型架构,尤其在自然语言处理(NLP)领域取得了显著的成功。Transformer模型最初由Google在2017年提出,旨在解决传统序列模型在处理长距离依赖问题上的不足。传统的RNN和LSTM模型在处理长文本序列时,容易出现梯度消失或爆炸问题,导致模型性能下降。而Transformer模型通过引入自注意力机制和多头注意力机制,成功地解决了这一问题。
Transformer模型在多个领域得到了广泛的应用,尤其是在自然语言处理(NLP)和计算机视觉(CV)等领域。以下是一些主要应用领域:
-
自然语言处理(NLP)
Transformer最初由Vaswani等人在2017年提出,用于解决自然语言处理任务。它通过自注意力机制捕捉句子中不同单词之间的关系,取得了显著的效果。Transformer在NLP的应用包括:- 机器翻译:Transformer在神经机器翻译中表现优异,显著提升了翻译质量。Google Translate等应用中广泛采用了Transformer模型。
- 文本生成:Transformer用于生成自然文本,如OpenAI的GPT(Generative Pre-trained Transformer)系列可以生成连贯的文章、对话等。
- 情感分析:用于判断文本的情感倾向,如正面或负面情感分析。
- 问答系统:如BERT(Bidirectional Encoder Representations from Transformers)可以用于构建强大的问答系统。
- 文本摘要:Transformer可用于自动生成长文本的摘要,帮助快速理解文档内容。
-
计算机视觉(CV)
虽然Transformer最初是为NLP设计的,但近年来它在计算机视觉中的应用也越来越广泛,尤其是自ViT(Vision Transformer)模型提出以来。应用包括:
- 图像分类:ViT使用Transformer结构直接对图像进行分类任务,打破了传统卷积神经网络(CNN)的垄断。
- 目标检测:通过将Transformer应用于目标检测任务,可以提高识别精度并减少依赖特征提取过程。
- 图像生成:使用Transformer生成高质量的图像,如文本到图像生成、图像修复等任务。
- 图像分割:通过捕捉图像中不同部分的关系,Transformer可以用于高精度的图像分割任务。
- 语音处理
Transformer也在语音处理领域取得了进展,常用于以下任务:
- 语音识别:如通过结合自注意力机制,Transformer可以提升语音转文本的准确率。
- 语音生成:如通过TTS(Text-to-Speech)系统,将文本生成自然流畅的语音。
- 语音增强:用以去噪和增强音频质量。
-
推荐系统
Transformer可以有效处理序列数据,因此也被应用于推荐系统中。通过学习用户行为序列(如点击记录、购买历史等),Transformer能够为用户提供个性化的推荐。 -
生物信息学
Transformer也逐渐在生物信息学领域崭露头角,尤其是蛋白质结构预测、DNA序列分析等方面。例如,AlphaFold(DeepMind的蛋白质结构预测模型)使用了Transformer模型来预测蛋白质的3D结构。 -
强化学习
在强化学习中,Transformer用于策略学习和环境建模。例如,使用Transformer处理时序数据,可以在复杂环境下实现更好的决策策略。 -
时序数据预测
Transformer被用于金融市场预测、天气预报、医疗诊断等时序数据的预测任务。通过捕捉长时间跨度的依赖关系,它在这类问题上表现得尤为出色。 -
跨模态任务
Transformer模型还被应用于多模态数据的融合和处理,例如:
- 图像-文本匹配:用于将图像和文本进行对应,如在搜索中根据图像生成文本描述。
- 视频理解:分析视频中的视觉和文本内容(如字幕、语音)以理解视频的整体语义。
- 游戏和自动化
Transformer在游戏中可用于理解和生成自然语言指令、剧情生成等。此外,在自动化领域,它可用于生成控制信号和优化任务调度等。
Transformer模型由于其强大的自注意力机制和并行处理能力,已经成为现代机器学习中不可或缺的工具,被广泛应用在多个领域,推动了这些领域的技术进步。
- 由输入部分、输出部分、编码器区域部分、解码器区域部分构成

2.词嵌入和位置编码
词嵌入
- 转换离散数据为连续数据自然语言处理中的文本数据本质上是离散的符号序列。例如,单词和字符是离散的,没有直接的数值表示。神经网络和其他机器学习算法通常处理的是连续的数值数据。因此,需要一种方法将这些离散的符号转换为连续的数值向量,这就是词嵌入的作用。
- 捕捉语义关系通过适当的训练,词嵌入可以捕捉到单词之间的语义关系。比如,经过训练的词嵌入向量可以使得“king”与“queen”的距离接近于“man”与“woman”的距离。这种特性使得词嵌入向量不仅能够表示单词本身,还能反映单词间的语义相似性。
位置编码
什么是位置编码?为什么我们需要位置编码。
对任何语言来说,句子中词汇的顺序和位置都是非常重要的。它们定义了语法,从而定义了句子的实际语义。RNN结构本身就涵盖了单词的顺序,RNN按顺序逐字分析句子,这就直接在处理的时候整合了文本的顺序信息。
但Transformer架构抛弃了循环机制,仅采用多头自注意机制。避免了RNN较大的时间成本。并且从理论上讲,它可以捕捉句子中较长的依赖关系。
由于句子中的单词同时流经Transformer的编码器、解码器堆栈,模型本身对每个单词没有任何位置信息的。因此,仍然需要一种方法将单词的顺序整合到模型中。
想给模型一些位置信息,一个方案是在每个单词中添加一条关于其在句子中位置的信息。我们称之为“信息片段”,即位置编码。
PE ( p o s , 2 i ) = sin ( p o s 1000 0 2 i d model ) PE ( p o s , 2 i + 1 ) = cos ( p o s 1000 0 2 i d model ) \text{PE}(pos, 2i) = \sin\left( \frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}} \right)\\\text{PE}(pos, 2i + 1) = \cos\left( \frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}} \right) PE(pos,2i)=sin(10000dmodel2ipos)PE(pos,2i+1)=cos(10000dmodel2ipos)
其中,
p
o
s
pos
pos 表示位置,
i
i
i 表示维度,
d
model
d_{\text{model}}
dmodel 是嵌入维度。
为什么用这个编码,验证可能性:
和角公式
s
i
n
(
α
+
β
)
=
s
i
n
α
c
o
s
β
+
c
o
s
α
s
i
n
β
,
c
o
s
(
α
+
β
)
=
c
o
s
α
c
o
s
β
−
s
i
n
α
s
i
n
β
sin(\alpha+\beta)=sin\alpha cos\beta+cos\alpha sin\beta,cos(\alpha+\beta)=cos\alpha cos\beta-sin\alpha sin\beta
sin(α+β)=sinαcosβ+cosαsinβ,cos(α+β)=cosαcosβ−sinαsinβ
假设我们有两个位置
x
x
x 和
y
y
y,并且定义:
f
(
i
)
=
1000
0
2
i
d
model
f(i)=10000^{\frac{2i}{d_{\text{model}}}}
f(i)=10000dmodel2i
有:
P
E
x
+
y
,
2
i
=
sin
(
x
+
y
f
(
i
)
)
=
sin
(
x
f
(
i
)
)
cos
(
y
f
(
i
)
)
+
cos
(
x
f
(
i
)
)
sin
(
y
f
(
i
)
)
P
E
x
+
y
,
2
i
+
1
=
cos
(
x
+
y
f
(
i
)
)
=
cos
(
x
f
(
i
)
)
cos
(
y
f
(
i
)
)
−
sin
(
x
f
(
i
)
)
sin
(
y
f
(
i
)
)
PE_{x+y,2i} = \sin\left(\frac{x + y}{f(i)}\right) = \sin\left(\frac{x}{f(i)}\right)\cos\left(\frac{y}{f(i)}\right) + \cos\left(\frac{x}{f(i)}\right)\sin\left(\frac{y}{f(i)}\right)\\PE_{x+y,2i+1} = \cos\left(\frac{x + y}{f(i)}\right) = \cos\left(\frac{x}{f(i)}\right)\cos\left(\frac{y}{f(i)}\right) - \sin\left(\frac{x}{f(i)}\right)\sin\left(\frac{y}{f(i)}\right)
PEx+y,2i=sin(f(i)x+y)=sin(f(i)x)cos(f(i)y)+cos(f(i)x)sin(f(i)y)PEx+y,2i+1=cos(f(i)x+y)=cos(f(i)x)cos(f(i)y)−sin(f(i)x)sin(f(i)y)
则:
P
E
x
+
y
,
2
i
=
P
E
x
,
2
i
⋅
P
E
y
,
2
i
+
1
+
P
E
x
,
2
i
+
1
⋅
P
E
y
,
2
i
+
1
P
E
x
+
y
,
2
i
=
P
E
x
,
2
i
+
1
⋅
P
E
y
,
2
i
+
1
−
P
E
x
,
2
i
⋅
P
E
y
,
2
i
PE_{x + y, 2i} = PE_{x, 2i }\cdot PE_{y, 2i+1} + PE_{x, 2i +1} \cdot PE_{y, 2i + 1}\\PE_{x + y, 2i} = PE_{x, 2i +1}\cdot PE_{y, 2i+1} - PE_{x, 2i } \cdot PE_{y, 2i }
PEx+y,2i=PEx,2i⋅PEy,2i+1+PEx,2i+1⋅PEy,2i+1PEx+y,2i=PEx,2i+1⋅PEy,2i+1−PEx,2i⋅PEy,2i
可以看出
T
r
a
n
s
f
o
r
m
e
r
Transformer
Transformer可以线性变换表示位置
x
x
x和
y
y
y之间的相对关系,这样构造出的线性关系可以表达各个位置的相对关系。
3.自注意力机制
- 自注意力机制,也称为内部注意力机制,允许模型在处理输入数据时,自动学习到不同位置之间的关联性,从而捕捉到更丰富的上下文信息。具体来说,它允许输入序列的每个元素都与序列中的其他元素进行比较,以计算序列的表示。
作用与优势
- 捕捉复杂依赖关系:自注意力机制使模型能够聚焦于输入序列中不同位置的关系,从而捕捉序列内的复杂依赖关系。这对于处理自然语言、语音和图像等序列数据尤为重要。
- 解决长距离依赖问题:传统的循环神经网络( R N N RNN RNN)在处理长序列时容易遇到梯度消失或梯度爆炸的问题,而自注意力机制可以有效地捕捉到序列中的长距离依赖关系。
- 并行计算:自注意力机制可以利用 G P U GPU GPU等硬件资源进行并行计算,从而大大提高了计算效率。
- 参数共享:在自注意力机制中,所有位置的权重共享相同的参数,这有助于减少模型的参数量和计算量。
结构图

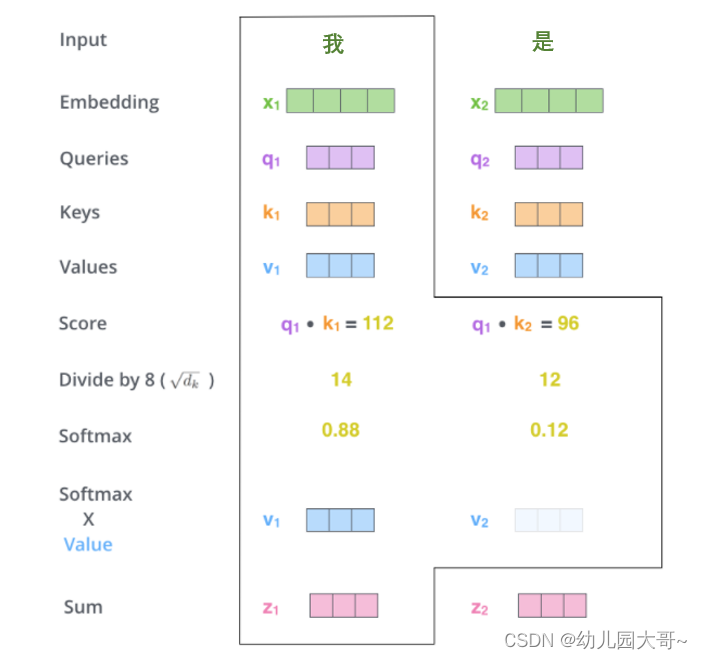
计算过程 - 从每个编码器的输入向量(每个单词的词向量,即Embedding)中生成三个向量,即查询向量、键向量和一个值向量。(这三个向量是通过词嵌入与三个权重矩阵即
W
Q
,
W
K
,
W
V
W^Q,W^K,W^V
WQ,WK,WV ,相乘后创建出来的)新向量在维度上往往比词嵌入向量更低。

以上所得到的查询向量、键向量、值向量组合起来就可以得到三个向量矩阵 Q u e r y 、 K e y s 、 V a l u e s Query、Keys、Values Query、Keys、Values。

- 计算得分
分数是通过所有输入句子的单词的键向量与当前的查询向量相点积来计算的

- 是将分数除以
8
8
8(
8
8
8是论文中使用的键向量的维数
64
64
64的平方根,这会让梯度更稳定。这里也可以使用其它值,
8
8
8只是默认值,这样做是为了防止内积过大。),然后通过
s
o
f
t
m
a
x
softmax
softmax传递结果。随着模型处理输入序列的每个单词,自注意力会关注整个输入序列的所有单词,帮助模型对本单词更好地进行编码。
s
o
f
t
m
a
x
softmax
softmax的作用是使所有单词的分数归一化,得到的分数都是正值且和为
1
1
1。

- 将每个值向量乘以
s
o
f
t
m
a
x
softmax
softmax分数(这是为了准备之后将它们求和)。这里的直觉是希望关注语义上相关的单词,并弱化不相关的单词(例如,让它们乘以
0.001
0.001
0.001这样的小数)。

- 使用注意力权重矩阵对值向量(
V
a
l
u
e
,
V
Value, V
Value,V)进行加权。具体来说,对于每个查询向量,将其对应的注意力权重与值向量矩阵中相应位置的向量进行相乘。
将所有加权后的值向量进行求和,得到该查询向量的新表示。这个过程是一个加权求和的过程,其中权重是注意力权重,而求和的对象是值向量。
4.多头注意力机制
- 有多个查询/键/值权重矩阵集合,( T r a n s f o r m e r Transformer Transformer使用八个注意力头)并且每一个都是随机初始化的。和上边一样,用矩阵 X X X乘以 W Q 、 W K 、 W V W^Q、W^K、W^V WQ、WK、WV来产生查询、键、值矩阵。 s e l f − a t t e n t i o n self-attention self−attention只是使用了一组 W Q 、 W K 、 W V W^Q、W^K、W^V WQ、WK、WV来进行变换得到查询、键、值矩阵,而 M u l t i − H e a d A t t e n t i o n Multi-HeadAttention Multi−HeadAttention使用多组 W Q 、 W K 、 W V W^Q、W^K、W^V WQ、WK、WV得到多组查询、键、值矩阵,然后每组分别计算得到一个 Z Z Z矩阵。
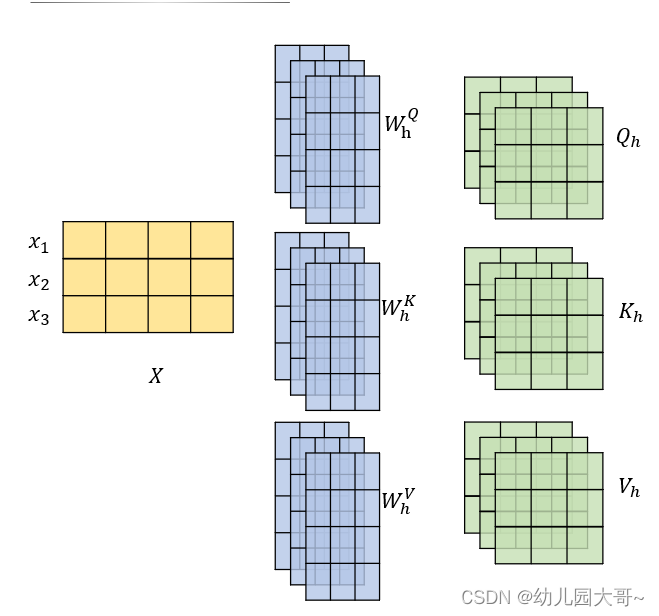
前馈层只需要一个矩阵,则把得到的
8
8
8个矩阵拼接在一起,然后用一个附加的权重矩阵
W
h
W^h
Wh与它们相乘。
总结整个流程

5.残差链接和层归一化
1. A d d Add Add部分
- 概念: A d d Add Add通常指的是残差连接( R e s i d u a l C o n n e c t i o n Residual Connection ResidualConnection)的加法操作。在神经网络中,尤其是在处理深层网络时,可能会出现训练困难、梯度消失或梯度爆炸等问题。残差连接通过允许原始输入信息直接流向更深层,有助于缓解这些问题。
- 实现:在 T r a n s f o r m e r Transformer Transformer的编码器和解码器的每一层中,通常包括一个自注意力机制( S e l f − A t t e n t i o n Self-Attention Self−Attention)层和一个前馈神经网络( F e e d − F o r w a r d N e u r a l N e t w o r k , F F N Feed-Forward\ Neural\ Network,FFN Feed−Forward Neural Network,FFN)。在这两个层之间,通过残差连接实现 A d d Add Add操作。具体来说,假设输入为 X X X,自注意力机制层的输出为 Z Z Z,则残差连接后的输出为 X + Z X+Z X+Z。
- 优点:残差连接使得网络在训练时能够更容易地学习到新的信息,同时保持原有信息不丢失。这有助于提升模型的性能,特别是在处理深层网络时。
2. Normalize部分
-
概念: N o r m a l i z e Normalize Normalize指的是归一化操作,它通常用于将数据转换为具有统一尺度的形式,以便模型更容易学习和处理。在 T r a n s f o r m e r Transformer Transformer中, N o r m a l i z Normaliz Normalize操作通常指的是 L a y e r N o r m a l i z a t i o n Layer\ Normalization Layer Normalization。
-
实现: L a y e r N o r m a l i z a t i o n Layer\ Normalization Layer Normalization是在每个样本的每个层内部进行的,而不是在整个批次( b a t c h batch batch)上进行的。具体来说,它计算每个样本在每个层上的激活值的均值和标准差,然后使用这些统计量来归一化激活值。这有助于加速训练过程并提升模型的性能。
-
优点: L a y e r N o r m a l i z a t i o n Layer\ Normalization Layer Normalization可以使得每一层的输出具有固定的尺度,从而加速训练过程。此外,它还可以减少内部协变量偏移( I n t e r n a l C o v a r i a t e S h i f t Internal\ Covariate\ Shift Internal Covariate Shift),即网络在训练过程中参数的变化导致每一层输入的分布发生改变的问题。
3. 总结: A d d & N o r m a l i z e Add\&Normalize Add&Normalize在 T r a n s f o r m e r Transformer Transformer中通过残差连接和 L a y e r N o r m a l i z a t i o n Layer\ Normalization Layer Normalization的结合,有效地提升了模型的训练效率和性能。残差连接使得模型能够更容易地学习新的信息并保持原有信息不丢失,而 L a y e r N o r m a l i z a t i o n Layer\ Normalization Layer Normalization则通过归一化操作加速了训练过程并减少了内部协变量偏移。
























 9万+
9万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








