图像处理算法 -- 3D-LUT插值算法之Matlab仿真

系列文章目录

图像处理算法 -- 3D-LUT插值算法之Matlab仿真

图像处理算法 -- 3D-LUT插值算法之FPGA实现

---

前言

        在图像处理领域中，经常会用到3D-LUT（3D-Look Up Table，三维查找表）来做颜色增强或者色彩转换。3D-LUT是一种处理视频色彩空间转换、非线性色域之间转换的有效手段，简单解释，就是将一组离散数值经过3D-LUT映射后转换为另一组离散数值。其处理效果如下面两个图所示。

图1 原图像

图2 3D-LUT映射后的图像

        本文主要就3D-LUT在工程应用领域中的Matlab仿真做简单介绍。

一、3D-LUT概念

        3D-LUT（三维查找表）被广泛地在电影工业和显示工业广泛使用，用在不同的显示器、不同的颜色空间之间做色彩校正、显示调节、效果和优化等方面。也就是说，3D-LUT实际上是颜色的转换，是RGB色彩空间的映射，借助3D-LUT的颜色映射，可以对图像/视频的颜色进行调节、校准，借助3D-LUT可以将输入的（R，G，B）像素映射为（R’，G’，B’）。

       3D-LUT表中包含了所有可能的（R、G、B）组合，表中的每一组元素包含了R、G、B三个分量的像素值。以8bit位深图像为例，对于一个色彩深度为8bit的RGB图像，3D-LUT表中一共需要有（2^8)^3组元素，每一组元素都包含了3个8bit的值（对应R、G、B三个通道）。在使用这样的一个3D-LUT处理图像时，需要先将这个LUT表存储在系统中，然后根据输入像素流中的每一个像素值，对LUT查表得到相应的元素，作为处理结果输出。这样的一个LUT最小需要占用的内存容量为：（2^8)^3*3*8bit = 402653184 bit = 48M Byte，对软/硬件系统来说就需要用48M Byte大小的内存来存储3D-LUT中的元素。而且，图像的色彩深度（通道位宽）越大，LUT表容量越大，所需要的内存容量也越大。 

色彩深度	内存容量
8bit	48M Byte
10bit	3.75G Byte
12bit	288G Byte

        例如，当R、G、B颜色的取值范围都是[0，0，0]到[255，255，255]时，如果要将这个映射完全存储起来，我们需要256^3条颜色信息与之对应，这个数据量是极其庞大的，不利于传播与使用。因此，使用采样的方法对LUT进行表示，然后在使用时通过插值处理对图像进行还原，可以有效降低LUT表的容量大小。例如，我们对整个颜色空间进行等分，使用32*32*32个立方体来代表整个RGB色彩空间，LUT中只存储这些等分端点的RGB值，这样就意味着需要有33^3个采样点来表示映射信息，使用33个采样点的意思是，在每个维度上使用33个采样点将256个颜色样本点等分成32个小的立体空间。但是这些点远远不能描述所有的像素值，因此，在使用3D-LUT时，先根据输入像素值找到其位于哪一个小的立方体内，然后再通过插值算法来估计出映射后的像素值。

从下图示意图可以发现，在3D-LUT中，沿着R、G、B方向，像素值是逐渐递增的。

       

        以色彩深度为8bit的3D-LUT表为例，稀疏化策略是：将一个含有（2^8)^3个点的立体空间沿着R、G、B等分成16个小的立方体，每个立方体的顶点视为一个晶格，则可以得到上图所示的尺寸为17*17*17大小的3D-LUT晶格模型。这样一来，3D-LUT表所需要的内存容量就减少为(17^3)*3*8bit ≈ 14.5K Byte，当尺寸为33*33*33时，内存容量为(33^3)*3*8bit ≈ 105.3K Byte，大大降低了对内存资源的依赖。常见的3D-LUT尺寸有17*17*17、33*33*33、65*65*65。

        显而易见的是，这样的3D-LUT显然在很多场景下都不适合使用，尤其是像基于FPGA这样的图像处理系统来说，FPGA片内存储器资源有限，往往只有十几K Byte至几M Byte的容量，例如：像ZYNQ Ultrascale+ MPSoC这种比较高端的FPGA芯片，至多也只有36Mbit URAM、35Mbit BRAM、11Mbit Distributed RAM，即使所有的RAM都用来存储LUT表也远远不够。因此，需要一种更轻量的3D-LUT表来解决容量大的问题。一个比较好的方法是对原有的3D-LUT表进行稀疏化，通过等间隔采样的方法，减少3D-LUT表中的数据量。        

        稀疏化操作有利于降低内存资源消耗，但是，会造成像素映射无法一一对应了。因为它是降采样抽取，输入的RGB值对应的位置往往是某几个点的中间位置，如果简单地取某个近似点的颜色是可行的，但是精度略差一些，通常的做法是计算输入像素值与LUT表中距离最近的晶格点的差值，重新融合计算。因此，在使用稀疏表处理图像时，需要利用3D-LUT表中已知的几个点，通过立体空间插值的方式得到结果，实现达到较高精度近似效果的同时降低系统对内存资源的消耗。比较常见的插值方法有三线性插值、四面体插值、金字塔插值等算法。

        插值算法在3D-LUT中扮演着重要的角色，通过对输入像素值和相邻数据点的计算关系进行合理的估计，实现对图像颜色和亮度的调整，同时输出图像更加真实和细腻。不同的插值算法有着不同的特点和适用范围，可以根据具体应用需求选择合适的算法。插值算法的选择和实现对于3D-LUT的效果和性能都有着重要的影响，因此在使用3D-LUT进行图像/视频处理时，插值算法的选择和优化是一个需要重视的问题。

        根据插值策略的不同，可以把三维立体空间插值分为三线性插值（八点六面体）、三棱柱插值（六点五面体）、金字塔插值（五点五面体）和四面体插值（四点四面体），这主要是根据切割立方体的不同方式来区分的。

二、3D-LUT的优势

         3D-LUT具有一些突出的特性和优势，3D LUT本身是查找表，将本该经过计算得到的映射结果预先存储下来，用于直接读取，避免了对像素点的映射计算，是一种空间换时间的算法，有高响应速度的保证；灵活程度大，带来更好的效果，常规的滤镜是单一映射，通常会将整个图像的所有像素机械地进行映射，例如，一个暖色调的普通滤镜会让图像内原本已经很暖的颜色变的更暖，甚至失真，而3D-LUT则可以实现控制，不同像素值会有不同的非线性的映射效果；支持硬件加速，高响应速度的图像处理通常需要GPU或FPGA进行加速，3D-LUT可以加载为纹理，通过OpenGL进行绘图风格和效果的自定义自由度大、简单LUT文件的制作比较简单，风格和效果可以由富有创意的艺术家们随心所欲地随时创建；用户自定义自由度大，用户可以随时下载或制作符合规范的LUT，在不修改软件的前提下，任意地设置LUT，实现不同的效果；兼容性高，3D-LUT实现的调色可以在任意没有接入调色功能的应用中（如系统应用、三方应用、浏览器、视频流、相机流），无感、无侵入的实现调色，被调色的目标不会出现任何兼容性问题，也没有任何侵入性，跨平台的移植性也很高。

三、插值算法分类

         三线性插值（八点六面体）

         与双线性插值原理类似，双线性插值是根据二维平面内正方形的4个顶点，进行3次线性插值计算得到新的插值点，而三线性插值是根据三维空间内立方体的8个顶点，进行7次线性插值得到新的插值点。

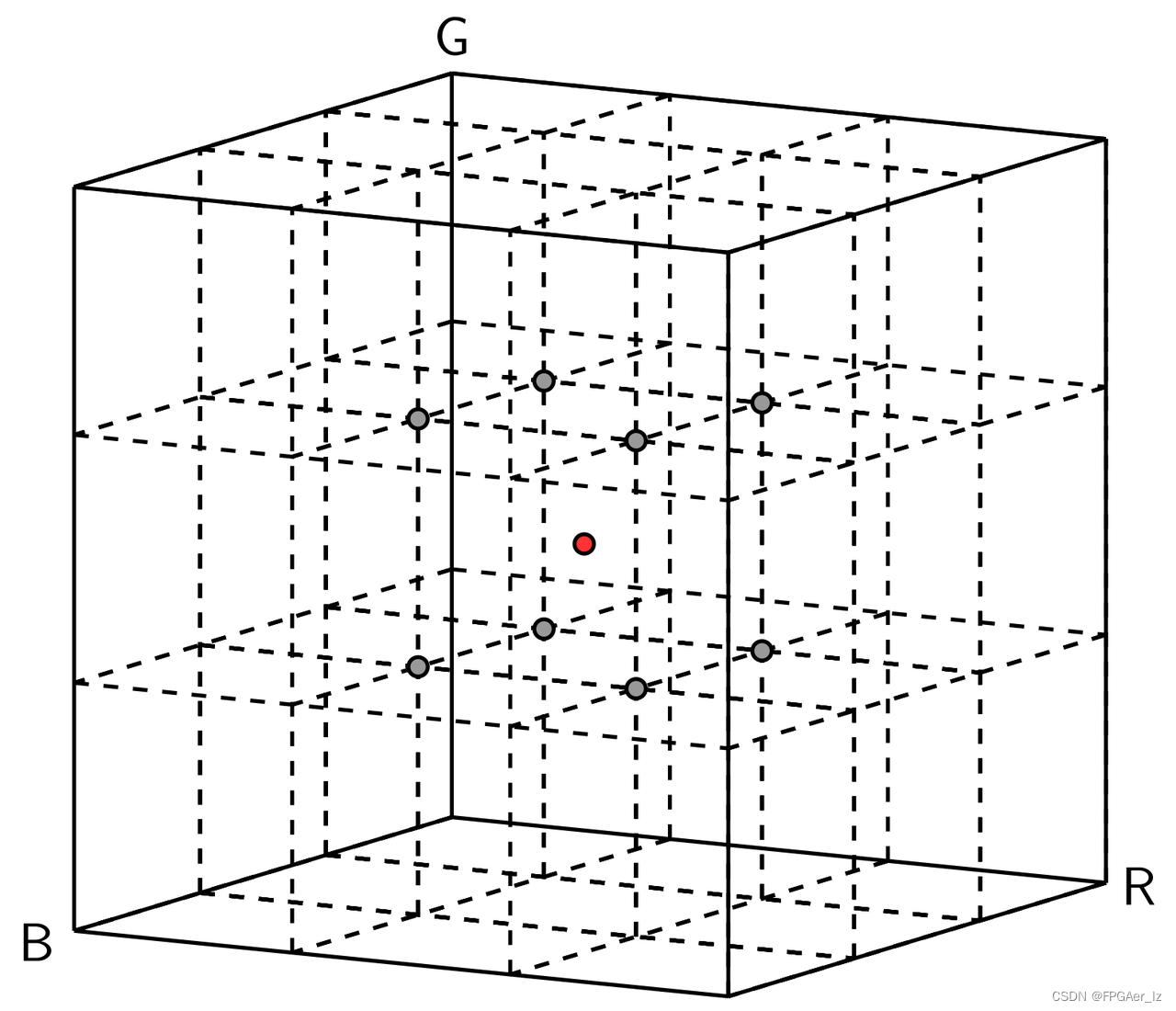
•         首先，沿着R轴进行插值得到2个蓝色点的值，利用灰色点（R0,G0,B1）和（R1,G0,B1）得到蓝色点（r,G0,B1）的值，同理可以得到其它3个蓝色点的值；

        

        

        

        

•         然后，沿着G轴进行插值得到2个绿色点的值，利用蓝色点（r,G0,B1）和（r,G1,B1）得到绿色点（r,g,B1）的值，同理可以得到另一个绿色点（r,g,B0）的值；

        

        

•         最后，沿着B轴进行插值得到红色点（r,g,b)值，利用两个绿色点（r,g,B1）和（r,g,B0）得到红色点（r,g,b）的值，就是最终的插值结果。

        

  其中，

  上述过程，可以用矩阵运算描述：