大学物理第十三章复习笔记：波动光学基础

大学物理第十三章：波动光学基础

一、光是电磁波

1.波源，波速，频率

波源：任何振动的电荷或者电荷系都是发射电磁波的源

波速：约等于3.0$\times 10^{8}m/s$

频率：光谱很宽，可见光为其中的一部分
$$\gamma 射线\to x射线\to 紫外线\to 可见光\to 红外线\to 无线电波$$

二、光源，光波的叠加

1.发光原理

由于某种原因（热辐射、电致发光、光致发光等），原子内部的运动状态发生变化，处于基态的原子吸收能量而到了激发态，但激发态的原子不稳定，它自发地从激发态跃迁到基态，并把多余的能量以电磁波的形式辐射出去，若$\lambda$在可见光范围，则物质发光。

2.注意：同一光源发出的光是非相干光

3.光波的叠加

（1）光束相干条件

• 同频
• 同振向
• 相位差恒定

合成光波的光强在空间形成强弱相间的稳定分布

• 不相干的两列光相遇：

  $I=I_1+I_2$--------亮度均匀

• 两束相干光束叠加：干涉条纹

  两相干波的振动方程分别为
  $$\begin{gathered} E_1=E_{10}cos(\omega t-2\pi \frac{r_1}{\lambda }+{\phi }_1) \\ {E}_2=E_{20}cos(\omega t-2\pi \frac{r_2}{\lambda }+{\phi }_2) \end{gathered}$$
  合成：
  $$\begin{gathered} E_0^2=E_{10}^2+E_{20}^2+2E_{10}{E}_{20}cos\Delta \phi \\ {I}_0^2=I_{10}^2+I_{20}^2+2\sqrt{I_{10}{I}_{20}}cos\Delta \phi \\ 当\Delta \phi ={\phi }_2-{\phi }_1-2\pi \frac{r_2-r_1}{\lambda }\{\begin{array}{l}2k\pi ，I_0^2=I_{10}^2+I_{20}^2+2\sqrt{I_{10}{I}_{20}}\\ (2k+1)\pi ，I_0^2=I_{10}^2+I_{20}^2-2\sqrt{I_{10}{I}_{20}}\end{array} \end{gathered}$$
  特别的，当${\phi }_1={\phi }_2，E_{10}=E_{20},I_1=I_2$时，我们引入光程差的概念

$$\delta =r_2-r_1=\{\begin{array}{l}k\lambda \\ (2k+1)\frac{\lambda }{2}\end{array}$$

4.如何获得相干光源

(1)分波阵面法

(2)分振幅法

三、杨氏双缝干涉实验（分波面法）

1.实验装置

2.相干光的获得：分波阵面法

3.屏幕显像

由于这样的装置，两束光的初相${\phi }_1,{\phi }_2$相同，所以振动加强和减弱仅取决于光程差$r_1,r_2$
$$\Delta \phi ={\phi }_2-{\phi }_1-2\pi \frac{r_2-r_1}{\lambda }，由波程差r_2-r_1决定$$

明暗条件：

$$\delta =r_2-r_1=\{\begin{array}{l}\pm k\lambda ，k=0,(中央明纹),k=1,2,...第1,2级明纹\\ (2k+1)\frac{\lambda }{2}，k=0,1,2,...第1,2，3级暗纹\end{array}$$

条纹位置：

$$\delta =r_2-r_1=dsin\theta \approx d\frac{x}{D}=\{\begin{array}{l}\pm k\lambda ，明纹\\ (2k+1)\frac{\lambda }{2}，暗纹\end{array}$$

明纹位置:

$$\{\begin{array}{l}{x}_{明}=\pm k\frac{D\lambda }{d}\\ x_{暗}=\pm (2k+1)\frac{D\lambda }{2d}\end{array}$$

条纹宽度：

$$\begin{gathered} 亮纹间距：\Delta x=(k+1)\frac{D\lambda }{d}-k\frac{D\lambda }{d}=\frac{D\lambda }{d} \\ 暗纹间距：\Delta x=\frac{D\lambda }{d} \end{gathered}$$

4.结论

（1）条纹特点

以中央明纹为中心，两侧条纹明暗相间，等宽度、等间距，等亮度

（2）条纹宽度公式

$\Delta x=\frac{D\lambda }{d}$

（3）不同频率的光照射

白光照射，$\lambda$不同，$\Delta x$不同。同一级光谱，由于$\lambda$ 不同，条纹位置不同，所以白光入射时，中央明纹是白色的，两侧条纹内紫外红排列.

（4）完整光谱级次

内紫外红：$k{\lambda }_{红}=(k+1){\lambda }_{紫}$;k可以看到完整光谱级次，k以上重叠起来

四、光程与光程差

1.光程

光在介质 中的波长${\lambda }_{介}=\frac{{\lambda }_0}{n}$

所以有
$$\Delta \phi =2\pi \frac{r_2}{{\lambda }_2}-2\pi \frac{r_1}{{\lambda }_1}=2\pi \frac{n_2{r}_2-n_1{r}_1}{{\lambda }_0}$$
所以相干条件转化为：
$$\delta =n_2{r}_2-n_1{r}_1=\{\begin{array}{l}\pm k\lambda ，k=0,(中央明纹),k=1,2,...第1,2级明纹\\ (2k+1)\frac{\lambda }{2}，k=0,1,2,...第1,2，3级暗纹\end{array}$$

2.透镜不会引起附加的光程差

五、薄膜干涉

1.薄膜干涉的种类

• 等厚干涉：厚度不均匀的表面形成的干涉条纹
• 等倾干涉：厚度均匀但入射角不同产生的干涉条纹

2.等厚干涉的一般计算

(1)光程差：

$$\delta =(|AB|+|BC|)n_2-CD{n}_1(\pm \frac{\lambda }{2}(半波损失项，无则不用，加减任选))$$

代入折射定律和几何关系后，得：
$$\delta =2d\sqrt{n_2^2-n_1^{2}si{n}^{2}i}(\pm \frac{\lambda }{2})$$

(2)光强

C点的光强确定于：
$$\delta =2d\sqrt{n_2^2-n_1^{2}si{n}^{2}i}(\pm \frac{\lambda }{2})=\{\begin{array}{l}k\lambda ,明纹\\ (2k+1)\frac{\lambda }{2}，暗纹\end{array}$$

(3)等厚干涉

若角度$i$不变，那么$\delta$只随厚度d变化，同一厚度对应同一级干涉条纹，所以称为等厚干涉

(4)半波损失项的确定

有无半波损失有$n_1,n_2,n_3$大小关系确定

有半波损失：
$$\{\begin{array}{l}{n}_1>n_2<n_3\\ n_1<n_2>n_3\end{array}$$
”三明治状“有半波损失

(5)公式中的k的取值

灵活取定，保证公式有意义，如d>0

(6)透射光也有干涉现象

二条透射光在薄膜下表面处相遇发生干涉，其光程差为：

$$\delta =(|AB|+|BC|)n_2-|CD|n_1(\pm \frac{\lambda }{2})=\{\begin{array}{l}k\lambda ,明纹\\ (2k+1)\frac{\lambda }{2}，暗纹\end{array}$$
(7)垂直入射的等厚干涉

3.劈尖干涉（垂直入射的等厚干涉）

（1）劈尖分类

• 空气劈尖
• 介质劈尖

（2）相干光的获得

入射光a入射到介质的表面，有反射光$a_1$和折射光$a_2$,$a_1，a_2$为分振幅得到的相干光

①空气劈尖相干条件

$$\delta =2nd+\frac{\lambda }{2}=\{\begin{array}{l}k\lambda ------k=1,2,...明纹\\ (2k+1)\frac{\lambda }{2}---k=0,1,2...暗纹\end{array}$$

注意：k的取值，当k=0时只能取暗纹，不能取明纹，保证d大于0，有意义

②常用结论

a.两级明纹对应的厚度差:

$$\begin{gathered} 2n{d}_{k+1}+\frac{\lambda }{2}=(k+1)\lambda \\ 2n{d}_k+\frac{\lambda }{2}=k\lambda \\ \therefore \Delta d=\frac{\lambda }{2n} \end{gathered}$$

厚度d上包含几个$\frac{\lambda }{2n}$，这个厚度上就有几个明条纹

同理相邻暗纹对应的厚度差：
$$\Delta d=\frac{\lambda }{2n}$$
相邻暗纹和明纹对应的厚度差：
$$\Delta d=\frac{\lambda }{4n}$$

b.条纹间距的变化

$$\begin{gathered} lsin\theta =\Delta d=\frac{\lambda }{2n} \\ l\theta \approx \frac{\lambda }{2n} \end{gathered}$$

• 所以，对于同一个劈尖：

$$\begin{gathered} \theta \uparrow \Rightarrow l\downarrow \\ \lambda \uparrow \Rightarrow l\uparrow \end{gathered}$$

• 随着$\theta$增大，条纹变密，向棱边靠拢

• 上玻璃片上移

$$\{\begin{array}{l}间距不变\\ 条纹整体向棱边移动\\ 棱边处发生：暗\to 亮\to 暗\to ...\end{array}$$

③劈尖的应用

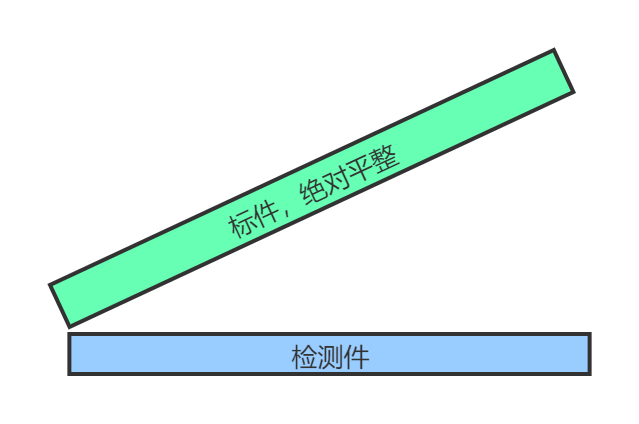
a.测量微小长度（上下玻璃片长度近似相同）

b.测量薄膜厚度

c.检测工件的平整度

4.增透膜（等厚干涉）

目的：尽量减少反射光强度引起的能量损失，从而得到更多的透射光

操作：在透镜表面上镀一层厚度均匀的膜，取适当的厚度 d 和折射率 n，使单色光在膜的二表面上的反射光发生干涉相消，而大部分能量透过膜使透射光增强，这样的膜称为增透膜

原理：单色平行光 a 从空气垂直射入$Mg{F}_2$ 薄膜，经薄膜上、下表面反射而在上表面相遇发生干涉。（d 处处相同，上表面无条纹，或亮或暗）

n2层为氟化镁，n3层为透镜，n1层为空气层

$n_3>n_2>n_1$，不会发生半波损失

光程差:$\delta =2n_{2}d$

为了使干涉相消：
$$\delta =2n_{2}d=\frac{\lambda }{2}(2k+1),k=0,1,...$$
当k=0时，取得最薄的厚度$\frac{\lambda }{4n_2}$

5.牛顿环（等厚干涉）

（1）实验装置

$$图5.5.1$$

（2）相干光的制备

分振幅法，与薄膜干涉相同

（3）定量计算

$$\delta =2nd+\frac{\lambda }{2}=\{\begin{array}{l}k\lambda ------k=1,2,...明纹\\ (2k+1)\frac{\lambda }{2}---k=0,1,2...暗纹\end{array}$$

中心点$\delta =0$为暗点

①两相邻明纹对应的厚度差

$$\Delta d=\frac{\lambda }{2n}$$

同理，两相邻暗纹对应的厚度差：
$$\Delta d=\frac{\lambda }{2n}$$

相邻明纹和暗纹之间的厚度差
$$\Delta d=\frac{\lambda }{4n}$$

②条纹间距

$$\begin{gathered} lsin\theta =\Delta d=\frac{\lambda }{2n} \\ l\approx \frac{\lambda }{2n\theta } \end{gathered}$$

劈尖$\theta$处处相同，条纹等间距

牛顿环$\theta$不同，条纹内疏外密

③干涉圆环的半径

由图5.5.1可得：
$$\begin{gathered} R^2=r^2+(R-d{)}^d=r^2+R^2-2Rd（高阶无穷小略去） \\ d=\frac{r^2}{2R} \end{gathered}$$
代入干涉条件：
$$\delta =2nd+\frac{\lambda }{2}=2n\frac{r^2}{2R}+\frac{\lambda }{2}=\{\begin{array}{l}k\lambda ------k=1,2,...明纹\\ (2k+1)\frac{\lambda }{2}---k=0,1,2...暗纹\end{array}$$
求得$r_{明}=...r_{暗}=...$

④明暗变化

• 牛顿环上移

  明暗交替，向中间收缩，中心点也明暗交替

• 牛顿环下移

  明暗交替向外扩散，中心点也明暗交替

六、迈克尔逊干涉仪（等厚干涉）

1.原理

直接理解成$M_1{M}_2^{\prime }$之间形成了空气薄膜即可

2.常用计算

迈克尔逊干涉仪各材料的使用保证不会发生半波损失：
$$\delta =2nd=\{\begin{array}{l}k\lambda \\ (2k+1)\frac{\lambda }{2}\end{array}$$

• $M_1{M}_2$严格垂直：

移动d，是整个视野变亮，暗。因为d处处相等。

• 稍有倾角

劈尖干涉，可以通过条纹移动条数来判断玻璃的移动距离
$$\Delta d=N\frac{\lambda }{2n}$$

• 插入别的介质

  引起光程差$\delta$的变化$\Delta \delta$

$$\Delta \delta =2nd-2n_{0}d=2d(n-1)$$

若有一根条纹移动$\Delta \delta =\lambda$

若有N跟条纹移动$\Delta \delta =N\lambda$
$$\begin{gathered} \Delta \delta =2nd-2n_{0}d=2d(n-1)=N\lambda \\ d=\frac{N\lambda }{n-1} \end{gathered}$$

七、惠更斯菲涅耳原理

1.光的衍射现象

光在前进过程中遇到障碍物，当障碍物的线度 d ~ $\lambda$时，光可以改变传播方向，绕过障碍物向其他方向传播，且光强重新分布。

2.惠更斯菲涅耳原理

• 惠更斯：子波概念
• 菲涅尔：光强变化修正

3.衍射的种类

$$\{\begin{array}{l}菲涅尔衍射\\ 夫琅禾费衍射，平行光衍射\end{array}$$

八、单缝的夫琅禾费衍射

1.实验装置

2.用半波带法分析条纹的形成

衍射角为$\phi$的一束衍射光，通过透镜汇聚于P点二条边缘光线的光程差$\delta =asin\phi$

通过半波带法分析，得到下面的结论:
$$\delta =asin\phi =\{\begin{array}{l}\pm 2k\frac{\lambda }{2}，k=1,2...暗纹\\ \pm (2k+1)\frac{\lambda }{2}，k=1,2...明纹\end{array}$$
明纹：衍射极大，衍射极强

暗纹：衍射极小，衍射极弱

• 不同的$\phi$，分成的半波带的面积不一样大
• 相同的$\phi$，分成的半波带的面积一样大

相邻二半波带的子波发出的光在 P 点干涉相消—暗纹；

明纹的亮度是由一个半波带的子波发出的光在P 点干涉叠加的结果
$$\begin{gathered} \phi 越大,BC越大，分成的半波带越多，一个半波带的面积越小，一个半波带所含的子波数目越少 \\ 明纹亮度越暗 \end{gathered}$$

3.条纹的计算

$$\begin{gathered} \delta =BC=asin\phi =atan\phi =a\frac{x}{f} \\ \delta =a\frac{x}{f}=\{\begin{array}{l}\pm 2k\frac{\lambda }{2}\\ \pm (2k+1)\frac{\lambda }{2}\end{array}k=1,2...k\ne 0 \end{gathered}$$

（1）明暗位置

$$\begin{gathered} x_{明}=\pm \frac{f\lambda }{2a}(2k+1) \\ {x}_{暗}=\pm \frac{f\lambda }{a}k \\ k=1,2,3... \end{gathered}$$

（2）条纹宽度

①中央明纹：o点两侧第一级暗纹的间距
$$\begin{gathered} k=1 \\ {x}_{1暗}=\frac{f\lambda }{a},x_{1暗}^{\prime }=-\frac{f\lambda }{a} \end{gathered}$$

②任意一级明纹宽度：任相邻两级暗纹宽度
$$\Delta x=x_{k+1暗}-x_{k暗}=\frac{f\lambda }{a}$$
中央明纹宽度是其他任意明纹宽度的两倍

（3）条纹位置的角坐标表示

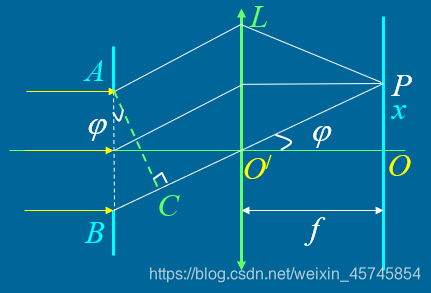
九、衍射光栅及光栅光谱

1.透射衍射光栅

（1）刻痕为不透光部分：b

（2）刻痕间的透光部分：a

（3）光栅常数：d=a+b

2.光栅衍射条纹特点及其成因

• 特点：细、亮、间距大；

• 成因：单缝衍射和多缝干涉叠加的结果

3.条纹分析

（1）中央明纹

通过每个缝的衍射角$\phi =0$的一束平行光，聚焦在主焦点上，因为$\delta =0$，所以形成中央亮纹

（2）各级明纹（主极大）的原因：光的干涉

$$\delta =(a+b)sin\phi =k\lambda ,k=0,\pm 1,\pm 2....光栅公式$$

（3）主极大的位置

①角位置
$$\begin{gathered} (a+b)sin\phi \approx (a+b)\phi =k\lambda \\ \Rightarrow \phi =\frac{k\lambda }{a+b} \end{gathered}$$
②用x表示：
$$\begin{gathered} (a+b)sin\phi \approx (a+b)tan\phi =(a+b)\frac{x}{f}=k\lambda \\ \Rightarrow x_{明}=\frac{kf\lambda }{a+b} \end{gathered}$$

（4）明纹出现的约束条件

①
$$\begin{gathered} |sin\phi |<1 \\ |k|<\frac{a+b}{\lambda } \end{gathered}$$
②缺级
$$\begin{gathered} (a+b)sin\phi =k\lambda ——满足缝间干涉加强 \\ asin\phi =k^{\prime }\lambda ——单缝衍射减弱点 \end{gathered}$$
此时，主极大消失，称为缺级，缺级的级数如下：
$$\begin{gathered} \frac{a+b}{a}=\frac{k}{k^{\prime }}\to k=k^{\prime }\frac{a+b}{a} \\ 若\frac{a+b}{a}为任意整数,k^{\prime }取\pm 1,\pm 2,... \end{gathered}$$
k值为缺级

4.光栅光谱

白光垂直入射，形成下面的光谱

（1）由光栅公式
$$\begin{gathered} (a+b)sin\phi =k\lambda ,k=0,\pm 1,\pm 2... \\ {x}_{明}=\frac{k\lambda f}{a+b} \end{gathered}$$
对于同一个k，不同的波长对应的明纹位置不同，所以是彩色条纹

（2）可见的光谱级数
$$|k|<\frac{a+b}{\lambda }$$
这里的$\lambda$指得是白光中的最长的波长

（3）可见的完整光谱数
$$\begin{gathered} (a+b)sin\phi =k{\lambda }_{红} \\ (a+b)sin\phi =(k+1){\lambda }_{紫} \\ 即(k+1){\lambda }_{红}=k{\lambda }_{紫} \end{gathered}$$
（4）总结

考察可见条纹，要考虑下面的两个方面：
$$\{\begin{array}{l}由于sin\phi 的有界性得到k的范围\\ 由于缺级损失的k\end{array}$$

十、光的偏振

1.光的偏振是横波的特有规律

（1）自然光概念

光振向取任何一个方向的概率均相等

（2）自然光的图形表示法

两个垂直方向的振动各占一半

二者疏密程度一样，表示各方向光振动一样，没有哪个方向的振动更占优势

（3）偏振光

①概念：只保留某一个方向，或者某一个方向的更占优势

②分类：
$$\{\begin{array}{l}完全偏振光（线偏振光）\\ 部分偏振光\end{array}$$
③获得偏振光的方法
$$\{\begin{array}{l}通过偏振片\\ 光在两个界面的反射\\ 双折射\end{array}$$

2.偏振片的起偏和检偏 马吕斯定律

（1）偏振片的性质

只能有一个方向的光，或者其他方向振动的光的分量通过。形成完全偏振光

光强减半

1°自然光通过偏振片A 成为偏振光，光强减半；转动 A，透射光强度不变。

2°自然光通过 A 成为偏振光，再通过 B，转动 B，透射光强度发生周期性变化：
$$\begin{gathered} 当A和B的偏振化方向一致，光强最强； \\ 当A和B的偏振化方向垂直，光强最弱； \end{gathered}$$

（2）马吕斯定律

设自然光强度$2I_0$，通过起偏器变为$I_0$ ，再通过检偏器，透射光的强度（不计吸收）：
$$I=I_{0}co{s}^2\alpha$$
结论：要使完全偏振光的偏振化方向转过90°必通过二块偏振光。

（3）反射和折射引起的偏振

①布儒斯特定律

当$i_b+\gamma =\frac{\pi }{2}$时完全偏振

当反射光垂直于折射光时完全偏振

此时：

• 反射光：完全偏振光，垂直于纸面
• 折射光：部分偏振光，入射面内的光振动强

$$tg{i}_b=\frac{n_2}{n_1}$$

应用：

• 测量不透明介质的折射率
• 玻璃堆

3.光的双折射

（1）晶体中的光的折射现象

在各向异性介质中，一束入射光可以产生两条折射光，一条为o光，一条为e光。此现象称为双折射

（2）双折射规律

• o光：遵守折射定律，寻常光
• e光：不遵守折射定律，非寻常光
• o光e光都是完全偏振光，二者振向相互垂直
• o光e光在同一介质中的传播速度不同
  • o光为球面波面
  • e光为旋转椭球面波面

（3）关于晶体的几个名词

• 晶体的光轴：不发生双折射的方向

• 单晶体&双晶体（光轴数量划分）

• 正晶体和负晶体

  • 正晶体：$v_o>v_e$，球面包椭球面

  • 负晶体：$v_e>v_o$，椭球面包球面

    

• 主平面：光轴和某一光线确定的平面

• 入射面：入射光和法线确定的平面

  • 当光轴在入射面内：o,e主平面重合
  • 当光轴垂直于入射面：o,e主平面不重合

o光垂直于o光主平面，e光与e光主平面平行