基于Matlab的非线性规划问题

1、题目

题目：
某集团拟在某市东、西、南、北建立4座超市，有10个候选位置Aj(j=1, 2, 3, … ,10)，考虑到各地区的消费水平及居住密度，规定如下：
(1) 东区由A1, A2, A3三个点中之多选择两个。
(2) 西区由A4, A5两个点中至少选择一个。
(3) 南区由A6, A7两个点中至少选一个。
(4) 北区由A8, A9, A10三个点中至少选两个。

试题说明：

问题1：

$A_j$各点的设备投资及每年可获利润由于地点不同而不一样，预测情况见表1(单位：万元)，总投资额不能超过720万元，问应该选择哪几个位置建立超市，可使年利润最大？

表格1 $A_j$各点投资与利润情况

项目	A1	A2	A3	A4	A5	A6	A7	A8	A9	A10
投资额	100	120	150	80	10	90	80	140	160	180
利润	35	40	50	22	20	30	25	48	58	61

问题2：

现在需要建立一个仓库给四个超市供货，为简化问题，假设仓库到每个超市是单独供货，即送完某个超市即返程，不再接着送下一个超市 (即仅考虑路程，不考虑图论)，且从仓库到各超市的运费单价一致，问该仓库建立在何处才能使超市的运输成本最低？

表格 2 $A_j$各点的位置情况

项目	A1	A2	A3	A4	A5	A6	A7	A8	A9	A10
x	67	-120	72	163	49	103	73	-30	29	-79
y	89	-115	-107	-81	-294	143	33	-75	137	-171

2、解析

问题1：

该集团拟定东南西北四个方向建立四座超市，从候选的10个位置中又根据各地区的消费水平和居住密度设定了一系列规则，在满足规则的同时使超市收益的年利率最大，由此我们构建了一个优化方程，最终通过matlab中的非线性规划fmincon函数求解，得出最终结果$A=(A_4,A_6,A_9,A_{10})$。

根据规定：
(1) 东区由A1, A2, A3三个点中之多选择两个。
(2) 西区由A4, A5两个点中至少选择一个。
(3) 南区由A6, A7两个点中至少选一个。
(4) 北区由A8, A9, A10三个点中至少选两个。
可得规划方程：
$$\{\begin{array}{l}{A}_1+A_2+A_3\le 2\\ A_4+A_5\ge 1\\ A_6+A_7\ge 1\\ A_8+A_9+A_{10}\ge 2\end{array}$$
$A_j$各点的设备投资及每年可获利润由于地点不同而不一样，总投资额不能超过720万元，可得规划方程：
$$\begin{array}{l}100\ast A_1+120\ast A_2+150\ast A_3+80\ast A_4+10\ast A_5+90\ast A_6+\cdots \\ 80\ast A_7+140\ast A_8+160\ast A_9+180\ast A_{10}\le 720\end{array}$$
要使年利润最大，则可得优化方程为：
$$\begin{array}{l}\max (35\ast A_1+40\ast A_2+50A_3+22\ast A_4+20\ast A_5+\cdots \\ 30\ast A_6+25\ast A_7+48\ast A_8+58\ast A_9+61\ast A_{10})\end{array}$$
通过matlab中的fmincon函数求解该非线性规划方程（代码见3代码求解）：
最终可得$A=(A_4,A_6,A_9,A_{10})$，且最大收益为$fval=171.0$。

问题2：

根据问题一中所得的四个超市坐标，选取配送成本最低的仓库坐标。考虑到本题中的超市是单独供货、送完即回，且运费单价一致，要使成本最低，只需要保证去往每个超市的路程的总和最小，则可以保证成本最低（这里假设每个超市配送的概率相同）。由此我们构建了路程的优化方程，使用与第一问相同的fmincon函数求解，得出最终结果$(x,y)=(105.5779,133.3760)$。

需要建立一个仓库给四个超市供货，由于是送完某个超市即返程，不再接着送下一个超市 (即仅考虑路程，不考虑图论)，且从仓库到各超市的运费单价一致，所以该问题求解达到每个超市的最短距离问题，可转换成求送往各个超市的距离的和最小问题，于是构建优化方程：
$$\min (\sum _{i=1}^4\sqrt{{(x-x_i)}^2+{(y-y_i)}^2})$$

通过matlab求解fmincon函数求解该非线性规划方程（代码见附页8.1.2）：

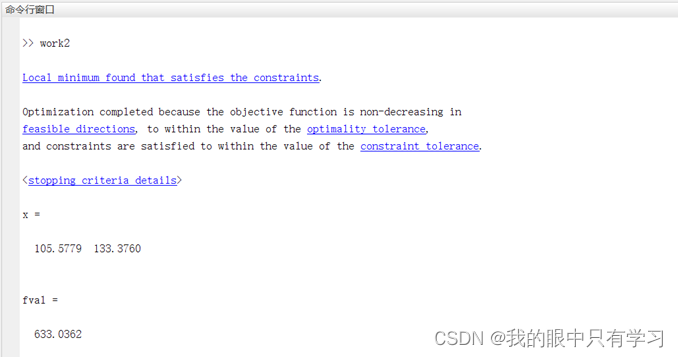
最终可得最优位置为$(x,y)=(105.5779,133.3760)$，各超市配送距离总和最小为$fval=633.0362$。

3、代码求解

问题1：

mycode1.m

% 优化方程
function f = mycode1(x)
f = -(35*x(1)+40*x(2)+50*x(3)+22*x(4)+20*x(5)+30*x(6)+25*x(7)+48*x(8)+58*x(9)+61*x(10));

work1.m

%% 非线性规划方程
% A1、A2...、A10
x0 = zeros(10,1);

% 对应方程1、2的左边
A = [1,1,1,1,1,1,1,1,1,1
    1,1,1,0,0,0,0,0,0,0
    0,0,0,-1,-1,0,0,0,0,0
    0,0,0,0,0,-1,-1,0,0,0
    0,0,0,0,0,0,0,-1,-1,-1
    100,120,150,80,10,90,80,140,160,180];
    
% 对应方程1、2的右边，注意fmincon是求小于，所以如果是大于的话就取负数就行（两边同时取负，不等式取反，基本常识）
b = [4;2;-1;-1;-2;720];

% 方程中的恒等关系，没有就像我这样取
Aeq = [];beq = [];

% x0的限制关系，0-1规划就需要取最小值为0，最大值为1
VLB = zeros(1,10);
VUB = ones(1,10);

% x为取值，fval为优化方程的最优解
[x, fval] = fmincon('mycode1',x0,A,b,Aeq,beq,VLB,VUB)

问题2：

mycode2.m

% 优化方程
function f = mycode2(x)

% 迭代的xi和yi
a = [163,103,129,-79];
b =  [-81,143,172,-171];
f1 = 0;

for i=1:4
    tmp = sqrt((x(1)-a(i))^2 + (x(2)-b(i))^2);
    f1 = tmp + f1;
end

f = f1;

work2.m

x0 = zeros(1,2);
A = [];
b = [];
Aeq = [];beq = [];
[x, fval] = fmincon('mycode2',x0,A,b,Aeq,beq)