电路分析基础

• 集总参数: 当电路的尺寸远小于其使用时最高工作频率所对应的波长时, 可以把元件的作用集总在一起, 用有限个R, L, C元件来描述时, 电路参数称集总参数.
• 分布参数: 当电路尺寸大于其使用时最高工作频率所对应的波长时, 电路中电压, 电流,不单是时间的函数, 还是空间的坐标的函数.
• 功率: 单位时间能量的变化,再关联方向下:
  $$p=\frac{dw}{dt}\to p=v\frac{dq}{dt}=vi$$
  若功率为正, 称为吸收功率, 消耗能量
  若功率为负, 称为输出功率, 提供能量
• 并联分流公式:$$i_n=\frac{G_n}{G_{eq}}i$$
• T型-$\Pi$型等效变换:
  
  
  
  
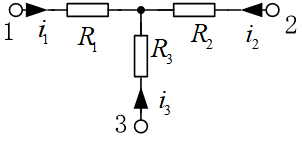
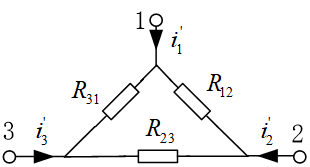
• 输入电阻: 不含独立电源(可含有受控源)的单口网络, 或双端口网络输入端口的电压和电流之比. (即从输入端口看的等 效电阻).

复数的表示

• 复数的一般表达方法为$F=a+bi$
• 欧拉公式: $e^{i\theta }=cos\theta +isin\theta$, 根据欧拉公式,有$$\begin{gathered} F=a+bi=|F|cos\theta +i|F|sin\theta =|F|e^{i\theta } \\ |F|=\sqrt{a^2+b^2},\theta =arctg\frac{b}{a} \end{gathered}$$
• 复数的极坐标表达方式:$F=|F|\angle \theta$
• 复数加减法.
  $$a_1+b_{1}i+a_2+b_{2}i=(a_1+a_2)+i(b_1+b_2)$$
  极坐标形式的负数加减可以用图示法计算.
• 复数乘除法–极坐标
  $$\begin{gathered} F_1=|F_1|\angle {\theta }_1,F_2=|F_2|\angle {\theta }_2 \\ {F}_1\cdot F_2=|F_1|e^{j{\theta }_1}\cdot |F_2|e^{j{\theta }_2}=|F_1||F_2|\angle {\theta }_1+{\theta }_2 \end{gathered}$$

正弦量的表示

• 正弦量的向量表示. 对于正弦量$$\begin{gathered} Icos(\omega x+\phi ) \\ 给e^{j(\omega x+\phi )}乘\sqrt{2}I,得到 \\ \sqrt{2}I{e}^{j(\omega x+\phi )}=\sqrt{2}Icos(\omega x+\phi )+\sqrt{2}jIsin(\omega x+\phi ) \end{gathered}$$
  其实部等于上面的正弦量, 因此可以使用$Re[\sqrt{2}I{e}^{j\theta }]$表达一个正弦量, $\sqrt{2}I{e}^{j\theta }$是复指数函数, 称为旋转相量.
• $$\begin{gathered} I(x)=Re[I{e}^{j(\omega x+\phi )}]=Re[I{e}^{j\omega x}{e}^{j\phi }] \\ 令\dot{I}=I{e}^{j\phi },带入上式,I(x)=Re[\dot{I}{e}^{j\omega x}] \\ \dot{I}=I{e}^{j\phi }=I\angle \phi \end{gathered}$$, $\dot{I}$称为$I{e}^{j\omega x}{e}^{j\phi }$的复振幅.用$\dot{I}$表示正弦量, 称其为正弦量的相量.
• 相量的微分性质.
  $$\begin{gathered} f(t)=\dot{F}=F\angle \varphi \\ {e}^{i\cdot \frac{\pi }{2}}=i \\ \frac{df}{dt}=j\omega \dot{F}=\omega F\angle (\varphi +90^o) \end{gathered}$$
• 电容电感的相量形式:

电容C:$$\begin{gathered} I=C\frac{dV}{dt} \\ v(t)=\sqrt{2}Vcos(\omega t+\phi )=Re[\dot{V}{e}^{j\omega t}] \\ i(t)=C\frac{dRe[\dot{V}{e}^{j\omega t}]}{dt}=Re[j\omega CV{e}^{j\omega t}], \\ \dot{I}=j\omega C\dot{V}=\omega V\angle (\varphi +90^o) \end{gathered}$$
电流超前电压90度.
电感L:
$$\begin{gathered} i(t)=\sqrt{2}Icos(\omega x+\varphi ) \\ V=L\frac{di(t)}{dt}=L\frac{dRe[\dot{I}{e}^{j\omega t}]}{dt} \\ =Re[j\omega L\dot{I}{e}^{j\omega t}] \\ \dot{V}=j\omega L\dot{I}=\omega LI\angle (\varphi +90^o) \\ \dot{I}=\frac{\dot{V}}{j\omega L} \end{gathered}$$
电压超前电流90度.

• 阻抗: 在具有电阻, 电容, 电感的电路中, 对电路电流所起的阻碍作用叫做阻抗. 阻抗常用Z表示, 是一个复数, 实部称为电阻, 虚部称为电抗. 电容在电路中对交流电所起的阻碍作用称为容抗, 电感对交流电起的阻碍作用称为感抗. 容抗和感抗总称为电抗. 阻抗的单位是欧姆.
• 电阻的阻抗只有实部, $Z_R=R$,电压与电流同相, R称为电阻.
• 电容的阻抗只有虚部, $Z_C=\frac{-1}{\omega C}$, 称为容抗, 电流超前电压90度.当$\omega$为0时, 容抗为$\infty$.
• 电感的阻抗只有虚部, $Z_L=j\omega L$,称为感抗, 电压超前电流90度, 当$\omega$为0时, 感抗为0.
• 导纳是电导和电纳的统称, 定义为阻抗的倒数, 符号为Y, 表示为$Y=G\pm jB$
• 串联电路中, 阻抗直接相加(电容阻抗为负).$$\begin{gathered} Z=R+j(\omega L-\frac{1}{\omega C}) \\ X=\omega L-\frac{1}{\omega C}网络电抗 \\ |Z|=\sqrt{R^2+X^2}阻抗的模 \\ {\varphi }_2=arctan\frac{X}{R}阻抗的幅角(阻抗角) \end{gathered}$$
  
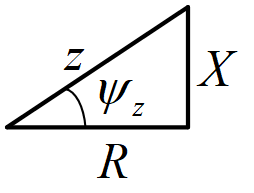
  阻抗角反映电压与电流的相位关系
  $\varphi >0$, 电压超前电流, 感性电路
  $\varphi <0$, 电流超前电压, 容性电路
  $\varphi =0$, 电压电流相同, 阻性电路
• 并联电路中, 导纳直接相加.

功率计算

• 平均功率(有功功率): 在电压,电流为关联参考方向下, 元件或单口网络的平均功率是瞬时功率在一个时间段内的平均值.定义为
  $$P=\frac{1}{t_2-t_1}{\int }_{t_1}^{t_2}p(t)dt=\frac{1}{t_2-t_1}{\int }_{t_1}^{t_2}v(t)\cdot i(t)dt$$

对于周期信号作用下的电路, 通常以一个周期内的平均功率进行衡量.
经计算, 平均功率的值为$VIcos\phi ,(\phi ={\varphi }_v-{\varphi }_i)$.是瞬时功率的恒定分量.其中,$\phi$称为功率因数角,$\lambda =cos\phi$称为功率因数.
平均功率表示单口网络实际消耗或产生的功率.
$$P=\frac{1}{T}{\int }_0^{T}p(t)dt=\frac{1}{T}{\int }_0^{T}v(t)\cdot i(t)dt$$

• 无功功率: 网络与外电源间能量交换的大小,用Q表示,$Q=VIsin\phi$.
• 视在功率: 单口网络端口电压有效值和电流有效值的乘积. 用S表示. S,P,Q之间满足直角三角关系: