MobileNetV2 网络详解以及Pytorch实现

本文主要针对MoblieNet V2，没有看过V1的也可以看，想看V3也可以先看本文。
先附上论文地址

V1      https://arxiv.org/abs/1704.04861
V2      https://arxiv.org/abs/1801.04381

深度可分离卷积

深度可以分离卷积（Depthwise separable convolution）在V1便被首次提出，之后的V2、V3都运用了这个。而使用深度可以分离卷积之后，唯一的好处就是极大的减小了参数的数量。

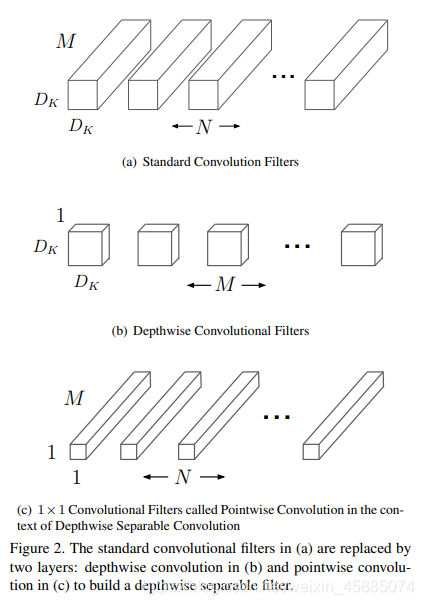
上文图片截取至V1的论文，可能不太直观。
普通的卷积是用一个卷积核同时对多个通道进行卷积操作，例如一张3x3x3的图片，经过一个普通卷积kernel_size = 3x3的卷积之后，它的尺寸就只有1x1x1。因为普通卷积的通道数目是默认和原图片一样的，即刚刚那个卷积实际大小是3x3x3。
但深度可分离卷积则是对单一通道的卷积。还是刚刚那张3x3x3图片，深度可分离卷积的kernel_size = 3x3。经过卷积之后，图片的尺寸是1x1x3。也就是说深度可分离卷积默认的通道数目只有1，即刚刚那个卷积的大小是3x3x1。
如果我们最终只想得到1x1x1的图片，我们就需要再使用一个kernel_size=1x1的普通卷积，让3个通道变为1个通道。

倒残差结构

倒残差结构(inverted residul block)是V1没有的，V2首创。我截取了原文论中对普通的残差结构和倒残差结构的差异的体现图。

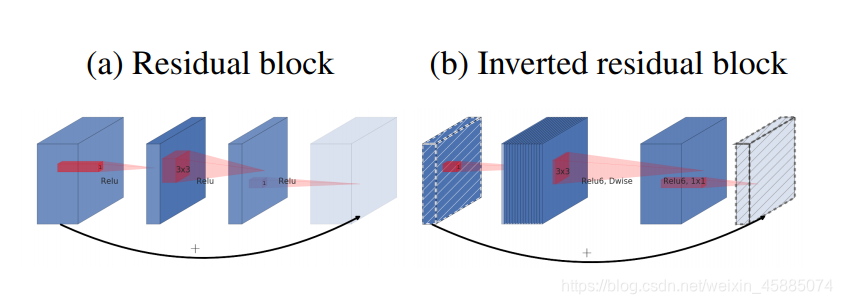
像这样，a是普通的残差结构，b是倒残差结构。可以看出，普通的残差结构是先通过卷积降维再升维度，而倒残差结构先升维再降维。

bottleneck具体实现

bottleneck就是结合了上文提到的深度可以分离卷积和倒残差结构的一个模块。
又被称为Bottleneck residual block。

上图有是源于原论文，其中k是输入通道数，t是拓展因子，也就是升维的倍率，s就是步长，k’是输出通道。dwise就是深度可分离卷积了。每一个dewise的kernel_size都是3x3。
原论文中有更直观的流程图，当Stride=1的时候才会出现残差边。

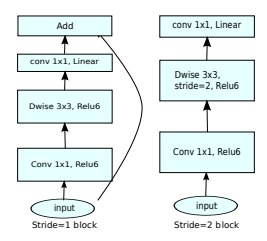
比较特殊的有两点
一：在最后一层卷积之后就没有激活函数了。
二：如果stride=1，且输入的通道和输出的通道不一样，要经过通道普通1x1卷积把通道扩展到k’才能和结果进行拼接的。
图解如下

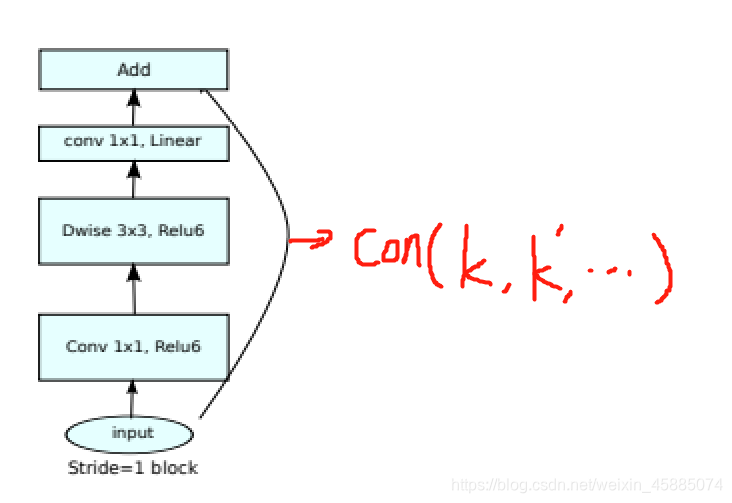
网络的具体结构

翻译过来就是，t表示扩展因子，c表示经过bottleneck之后的输出通道，n表示重复操作bottleneck的次数，s表示进入bottleneck之后第一个卷积的步长（剩下的步长都为1），最后的k就是你想分类的数目咯。

Pytorch构建bottleneck

import torch.nn as nn
import torch.nn.Functional as F


class bollteneck(nn.Module):
    def __init__(self, in_channels, out_channels, t, stride):
        super(bollteneck, self).__init__()
        self.stride = stride
        expansion = in_channels*t     # t是拓展因子
        self.conv1 = nn.Conv2d(in_channels, expansion, kernel_size=1)
        self.bn1= nn.BatchNorm2d(expansion)
        self.dwise = nn.Conv2d(expansion, expansion, kernel_size=3, groups=expansion, stride=stride, padding=1)         #当groups=expansion，这个卷积就是深度可分离卷积了
        self.pointwise = nn.Conv2d(expansion, out_channels, kernel_size=1)
        self.bn2 = nn.BatchNorm2d(out_channels)

        self.shortcut = nn.Sequential()
        if stride == 1 and in_channels != out_channels:
            self.shortcut = nn.Sequential(
                nn.Conv2d(in_channels, out_channels, kernel_size=1),
                nn.BatchNorm2d(out_channels),
            )

    def forward(self, x):
        feat1 = F.relu6(self.bn1(self.conv1(x)))
        feat2 = F.relu6(self.bn1(self.conv1(feat1)))
        out = self.bn2(self.pointwise(feat2))
        out = out+self.shortcut(x) if self.stride == 1 else out

        return out

Pytorch 主干网络

class MainNet(nn.Module):
    def __init__(self, num_classes):
        super(MainNet, self).__init__()
        self.conv1= nn.Conv2d(3, 32, kernel_size=3, stride=2, padding=1)
        self.bn1 = nn.BatchNorm2d(32)
        list = [[1, 16, 1, 1],
               [6, 24, 2, 2],
               [6, 32, 3, 2],
               [6, 64, 4, 2],
               [6, 96, 3, 1],
               [6, 160, 3, 2],
               [6, 320, 1, 1]]
        self.millde_layers = self.make_layers(list)
        self.conv2 = nn.Conv2d(320, 1280, kernel_size=1)
        self.bn2 = nn.BatchNorm2d(1280)
        self.avg = nn.MaxPool2d(kernel_size=7)
        self.linear = nn.Linear(1280, num_classes)

    def make_layers(self, list):
        layers = []

        for i in range(7):
            n = list[i][2]
            for x in range(n):
                t = list[i][0]
                if i >= 1:
                    in_channles = list[i-1][1]
                else:
                    in_channles = 32
                out_channles = list[i][1]
                stride = list[i][3]
                if n >= 1 and i >= 1:
                    in_channles = out_channles
                bollteneck(in_channles, out_channles, t, stride)
                layers.append(bollteneck)

        return nn.Sequential(*layers)

    def forward(self, image):
        feat1 = F.relu6(self.bn1(self.conv1(image)))
        feat2 = self.millde_layers(feat1)
        feat3 = F.relu6(self.bn2(self.conv2(feat2)))
        feat4 = self.avg(feat3)
        all = feat4.view(feat4.shape(0), -1)
        out = self.linear(all)

        return out