启发式图搜索策略

启发式策略

什么是启发式信息？

用来简化搜索过程有关具体问题领域的特性的信息叫做启发信息。
启发式图搜索策略（利用启发信息的搜索方法）的特点：重排OPEN表，选择最有希望的节点加以扩展。
种类：A、A*算法等。

运用启发式策略的两种基本情况：

（1）一个问题由于存在问题陈述和数据获取的模糊性，可能会使它没有一个确定的解。
（2）虽然一个问题可能有确定解，但是其状态空间特别大，搜索中生成扩展的状态数会随着搜索的深度呈指数级增长。

例5.6 一字棋。

在九宫棋盘上，从空棋盘开始，双方轮流在棋盘上摆各自的棋子  或  （每次一枚），谁先取得三子一线（一行、一列或一条对角线）的结果就取胜。



启发式策略的运用

启发信息和估价函数

在具体求解中，能够利用与该问题有关的信息来简化搜索过程，称此类信息为启发信息。
启发式搜索：利用启发信息的搜索过程。

求解问题中能利用的大多是非完备的启发信息：

（1）求解问题系统不可能知道与实际问题有关的全部信息，因而无法知道该问题的全部状态空间，也不可能用一套算法来求解所有的问题。
（2）有些问题在理论上虽然存在着求解算法，但是在工程实践中，这些算法不是效率太低，就是根本无法实现。

按运用的方法分类：

1. 陈述性启发信息：用于更准确、更精炼地描述状态
2. 过程性启发信息：用于构造操作算子
3. 控制性启发信息：表示控制策略的知识

按作用分类：

1. 用于扩展节点的选择，即用于决定应先扩展哪一个节点，以免盲目扩展。
2. 用于生成节点的选择，即用于决定要生成哪些后继节点，以免盲目生成过多无用的节点。
3. 用于删除节点的选择，即用于决定删除哪些无用节点，以免造成进一步的时空浪费。
   估价函数（evaluation function）：估算节点“希望”程度的量度。
   估价函数值 f(n) ：从初始节点经过 n节点到达目标节点的路径的最小代价估计值，其一般形式是
   

g(n)：从初始节点 S0 到节点 n 的实际代价 ；
h(n)：从节点 n 到目标节点 Sg 的最优路径的估计代价，称为启发函数。
h(n) 比重大：降低搜索工作量，但可能导致找不到最优解；
h(n) 比重小：一般导致工作量加大，极限情况下变为盲目搜索，但可能可以找到最优解。

例5.7 八数码问题的启发函数：

启发函数1: 取一棋局与目标棋局相比，其位置不符的数码数目，例如 h(S0) = 5;
启发函数2: 各数码移到目标位置所需移动的距离的总和,例如 h(S0) =6;
启发函数3：对每一对逆转数码乘以一个倍数, 例如3倍，则h (S0) =3;
启发函数4：将位置不符数码数目的总和与3倍数码逆转数目相加，例如 h (S0) =8。

A搜索算法

A 搜索算法：使用了估价函数 f 的最佳优先搜索。
OPEN表：保留所有已生成而未扩展的状态；
CLOSED表：记录已扩展过的状态。
估价函数 f(n) = g(n) +h(n)
如何寻找并设计启发函数 h(n) ，然后以 f(n) 的大小来排列OPEN表中待扩展状态的次序，每次选择 f(n) 值最小者进行扩展。
g(n)：状态n的实际代价，例如搜索的深度；
h(n)：对状态n与目标“接近程度”的某种启发式估计。

A 算法流程图

例5.8 利用 A 搜索算法求解八数码问题，问最少移动多少次就可达到目标状态？
估价函数定义为 f(n) = g(n) + h(n )
g(n)：节点 n 的深度，如 g (S0)=0。 h(n)：节点 n 与目标棋局不相同的位数（包括空格），简称“不在位数”，如 h (S0)=5。

操作算子集： ↑, ↓, →, ←

问题：A搜索算法能不能保证 找到最优解（路径最短的解）？
g(n)：从初始节点 S 到节点 n 的实际代价 ；
h(n)：对状态n与目标节点接近程度的某种启发式估计

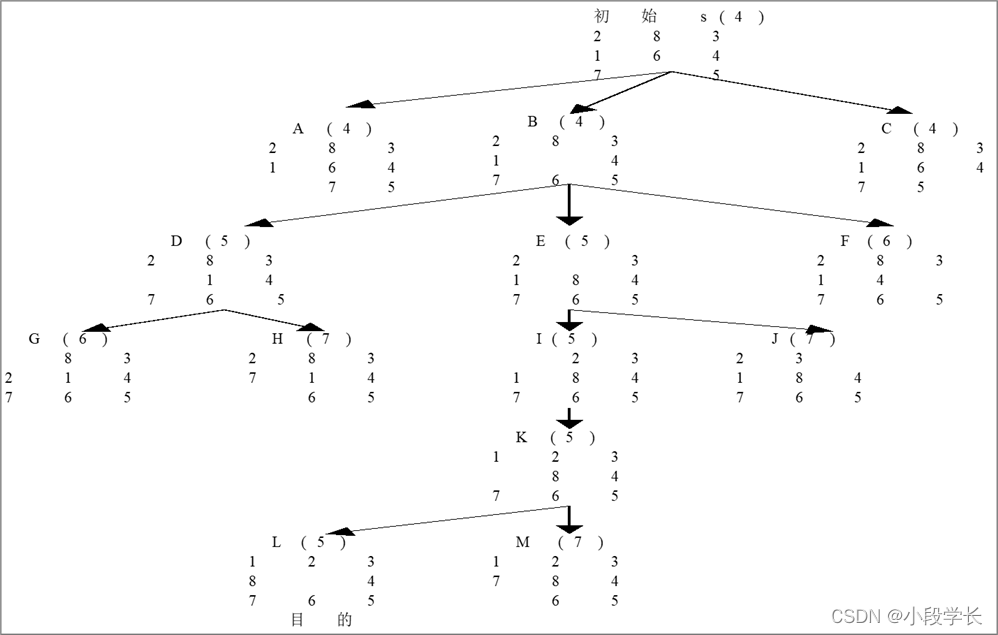
A*搜索算法及其特性分析

如果某一问题有解，那么利用A搜索算法对该问题进行搜索则一定能搜索到解，并且一定能搜索到最优的解而结束。
上例中的八数码A搜索树也是A搜索树，所得的解路（s，B，E，I，K，L）为最优解路，其步数为状态L（5）上所标注的5 。

可采纳性

当一个搜索算法在最短路径存在时能保证找到它，就称该算法是可采纳的。
A搜索算法是可采纳的。
A搜索算法( h(n)=0 )

单调性

A搜索算法并不要求g(n)=g(n)，则可能会沿着一条非最佳路径搜索到某一中间状态。
如果对启发函数h(n)加上单调性的限制，就可以总从祖先状态沿着最佳路径到达任一状态。
如果某一启发函数h(n)满足：
1）对所有状态ni和nj，其中nj是ni的后裔，满足h(ni)-h(nj)<=cost(ni, nj)，其中cost(ni, nj)是从ni到nj的实际代价。
2）目的状态的启发函数值为0。
则称h(n)是单调的。
A*搜索算法中采用单调性启发函数，可以减少比较代价和调整路径的工作量，从而减少搜索代价。

信息性

在两个A启发策略的h1和h2中，如果对搜索空间中的任一状态n都有h1(n) ≤ h2(n)，就称策略h2比h1具有更多的信息性。
如果某一搜索策略的h(n)越大，则A算法搜索的信息性越多，所搜索的状态越少。
但更多的信息性需要更多的计算时间，可能抵消减少搜索空间所带来的益处。
欢迎大家加我微信交流讨论（请备注csdn上添加）