💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
铰接式车辆横向动力学仿真与车辆模型研究
一、铰接式车辆的定义及结构特点
铰接式车辆是一种通过刚性或柔性铰接机构连接多个车体或车架的复杂多体系统,其核心特征是通过铰接点实现车体间的相对运动,从而提升转弯灵活性和环境适应性。主要分为铰接列车、工程机械(如装载机、自卸车)、铰接卡车等类别。
1. 结构特点
- 铰接装置类型:
- 转盘式:通过转盘轴承连接车体,适用于高速列车(如TGV),支撑稳定且回转阻力低(图7)。
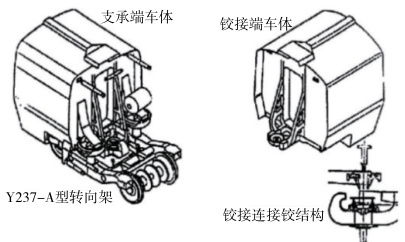
- 橡胶关节式:利用橡胶材料的弹性实现缓冲和减震,常见于轻轨车辆(图8)。
- 橡胶球心盘式:结合球铰与橡胶堆,提供多向自由度,适用于重载工程车辆(图9)。
- 转盘式:通过转盘轴承连接车体,适用于高速列车(如TGV),支撑稳定且回转阻力低(图7)。
- 承载方式:
- 摇枕两点承载(如Talgo列车)、无摇枕四点承载等,影响车辆动态响应和结构强度。
- 转向机构:
- 液压油缸驱动前后车架相对转动,形成折腰转向,常见于工程车辆(如装载机)。
2. 优势与挑战
- 优势:减少转向架数量(如铰接列车每两节车厢共用1个转向架),降低重量、制造成本及运行阻力;提升曲线通过能力(转弯半径减少30%-50%)。
- 挑战:横向刚度低导致稳定性差,转向迟滞现象显著,尤其在低附着路面易引发侧翻。
二、横向动力学建模方法
铰接式车辆的横向动力学模型需综合考虑车体间耦合运动、轮胎力非线性特性及控制策略的影响,建模流程如下:
1. 建模步骤
- 几何模型定义:
- 使用CAD(如AutoCAD)或多体动力学软件(ADAMS、Simpack)建立3D模型,定义质量、惯性参数、轮胎特性等(图3)。
- 自由度分析:
- 基础模型:4自由度(前车体纵向、侧向、横摆;后车体横摆)。
- 扩展模型:8自由度(增加车轮旋转自由度),适用于分布式驱动车辆。
- 运动学方程:
- 通过坐标系转换建立前后车体质心位置关系(式1),推导等效侧偏角、曲率半径等参数:

- 动力学方程:
- 考虑液压转向力矩(式2)、轮胎侧向力(如Pacejka模型)及铰接点受力平衡:

- 控制策略:
- 直接横摆力矩控制(DYC) :基于质心侧偏角和横摆角速度反馈,调节驱动力分配。
- 双通道控制:分离转向跟随与横摆稳定性补偿,提升低附着路面性能。
2. 关键模型验证
- 实验对比:通过比例样机测试转向角、横向加速度等参数,验证模型对转向迟滞现象的捕捉精度(图8)。
- 仿真验证:使用MATLAB/Simulink或硬件在环(HIL)平台模拟J型转弯、双移线等工况,误差<3%。
三、现有仿真软件支持情况
| 软件名称 | 适用场景 | 功能特点 | 案例引用 |
|---|---|---|---|
| ADAMS | 多体动力学分析 | 支持8自由度非线性模型,集成液压系统与轮胎模型 | 铁水罐车曲线通过性能分析 |
| MATLAB/Simulink | 控制策略开发与实时仿真 | 可嵌入主动转向算法(如横摆补偿),支持硬件在环测试 | 泵控电液转向系统验证 |
| CarSim | 车辆动力学参数化建模 | 提供预置铰接车辆模板,快速调整悬架与转向参数 | 铰接客车稳定性仿真 |
| Simpack | 铁路与重载车辆仿真 | 支持铰接列车轴重分配与临界速度计算 | 铰接式铁水罐车动力学分析 |
四、最新研究进展与未来方向
- 实时仿真技术:
- 提升模型计算效率以支持自动驾驶硬件在环(HIL)测试,缩短开发周期。
- 多物理场耦合:
- 集成热-机-液耦合效应,模拟极端工况下的结构变形与油液泄漏影响。
- 智能控制算法:
- 多环嵌套控制:结合位置-速度双闭环与横摆补偿,提升差动转向车辆的轨迹跟踪精度。
- 深度强化学习:通过端到端训练优化铰接角与驱动力分配,适应非结构化环境。
- 新型铰接机构设计:
- 柔性材料(如形状记忆合金)与主动阻尼器的结合,减少转向冲击载荷。
五、结论
铰接式车辆横向动力学仿真的核心在于精确建模与多学科协同优化。未来研究需进一步结合高精度传感器数据与AI算法,推动其在自动驾驶与特殊运输领域的应用。仿真工具的模块化与开源化(如ROS兼容性)将是提升研究效率的关键。
📚2 运行结果

















部分代码:
%% Maneuver
% The maneuver to be estimated by the Kalman Filter is defined here.
%
% Choosing simulation parameters:
%
T = 6; % Total simulation time [s]
resol = 50; % Resolution
TSPAN = 0:T/resol:T; % Time span [s]
%%
% Running simulation.
%
simulatorPlant = Simulator(VehiclePlant, TSPAN);
simulatorPlant.dPSI0 = 0.35;
simulatorPlant.Simulate
%%
% Printing simulation parameters.
%
disp(simulatorPlant)
%%
% Retrieving states
%
XTPlant = simulatorPlant.XT;
YTPlant = simulatorPlant.YT;
PSIPlant = simulatorPlant.PSI;
vTPlant = simulatorPlant.VEL;
ALPHATPlant = simulatorPlant.ALPHAT;
dPSIPlant = simulatorPlant.dPSI;
XOUTPlant = [XTPlant YTPlant PSIPlant vTPlant ALPHATPlant dPSIPlant];
%%
% Generating graphics of the vehicle in the considered maneuver (plant)
%
gPlant = Graphics(simulatorPlant);
gPlant.TractorColor = 'r';
gPlant.Frame();
%%
%
close all % Closing figures
%% Modelo
% O modelo utilizado no algoritmo de estima玢o � baseado no mesmo modelo
% f韘ico considerado no modelo da planta. Al閙 disso, o modelo parte da
% premissa de que o projetista do estimador n鉶 tem conhecimento adequado
% da curva caracter韘tica do pneu. Logo, o modelo de ve韈ulo � igual ao
% utilizado na planta, por閙, o modelo de pneu � dado pelo modelo linear
% Tire linear, resultando num modelo do sistema de menor complexidade (em
% rela玢o � planta) e com mais hip髏eses simplificadoras.
%
% Inicializando o pneu
%
TireModel = TireLinear;
disp(TireModel)
%%
% Choosing model vehicle
%
VehicleModel = VehicleSimpleNonlinear; % Same as plant
VehicleModel.tire = TireModel;
disp(VehicleModel)
%%
% Simulador com o mesmo vetor TSPAN e simula玢o
%
simulatorModel = Simulator(VehicleModel, TSPAN);
simulatorModel.dPSI0 = 0.35;
simulatorModel.Simulate;
disp(simulatorModel)
%%
% Retrieving states
%
XTModel = simulatorModel.XT;
YTModel = simulatorModel.YT;
PSIModel = simulatorModel.PSI;
vTModel = simulatorModel.VEL;
ALPHATModel = simulatorModel.ALPHAT;
dPSIModel = simulatorModel.dPSI;
%%
% A manobra gerada pelo modelo escolhido pelo projetista a partir da mesma
% condi玢o inicial � ilustrada na figura a seguir
%
gModel = Graphics(simulatorModel);
gModel.TractorColor = 'g';
gModel.Frame();
%%
%
close all % Closing figures
%% Plant and model comparison
% Comparando o modelo de pneu
%
g = 9.81;
FzF = VehiclePlant.mF0*g;
FzR = VehiclePlant.mR0*g;
muy = VehiclePlant.muy;
nF = VehiclePlant.nF;
nR = VehiclePlant.nR;
alpha = 0:0.5:15;
alpha = alpha*pi/180;
FyLin = - TireModel.Characteristic(alpha);
FyFPac = - TirePlant.Characteristic(alpha, FzF, muy);
FyRPac = - TirePlant.Characteristic(alpha, FzR, muy);
figure
ax = gca;
set(ax,'NextPlot','add','Box','on','XGrid','on','YGrid','on')
plot(alpha(1:floor(end/2))*180/pi,FyLin(1:floor(end/2)),'r')
plot(alpha*180/pi,FyFPac,'g')
plot(alpha*180/pi,FyRPac,'g--')
xlabel('alpha [deg]')
ylabel('Fy [N]')
l = legend('Linear','Pacejka F','Pacejka R');
set(l,'Location','SouthEast')
%%
% Comparando os estados
figure
ax = gca;
set(ax,'NextPlot','add','Box','on','XGrid','on','YGrid','on')
plot(TSPAN,XTPlant,'r')
plot(TSPAN,XTModel,'r--')
xlabel('Time [s]')
ylabel('Distance X [m]')
figure
ax = gca;
set(ax,'NextPlot','add','Box','on','XGrid','on','YGrid','on')
plot(TSPAN,YTPlant,'g')
plot(TSPAN,YTModel,'g--')
xlabel('Time [s]')
ylabel('Distance Y [m]')
figure
ax = gca;
set(ax,'NextPlot','add','Box','on','XGrid','on','YGrid','on')
plot(TSPAN,PSIPlant,'b')
plot(TSPAN,PSIModel,'b--')
xlabel('Time [s]')
ylabel('PSI [rad]')
figure
ax = gca;
set(ax,'NextPlot','add','Box','on','XGrid','on','YGrid','on')
plot(TSPAN,vTPlant,'c')
plot(TSPAN,vTModel,'c--')
xlabel('Time [s]')
ylabel('vT [m/s]')
figure
ax = gca;
set(ax,'NextPlot','add','Box','on','XGrid','on','YGrid','on')
plot(TSPAN,ALPHATPlant,'m'),
plot(TSPAN,ALPHATModel,'m--'),
xlabel('Time [s]')
ylabel('ALPHAT [rad/s]')
figure
ax = gca;
set(ax,'NextPlot','add','Box','on','XGrid','on','YGrid','on')
plot(TSPAN,dPSIPlant,'k')
plot(TSPAN,dPSIModel,'k--')
xlabel('Time [s]')
ylabel('dPSI [rad/s]')
%%
% Comparando a acelera玢o longitudinal e transversal
saidasPlant = [XTPlant YTPlant PSIPlant vTPlant ALPHATPlant dPSIPlant];
matDerivEstadosPlant = zeros(size(saidasPlant));
for i = 1:size(saidasPlant,1)
auxil = simulatorPlant.Vehicle.Model(1,saidasPlant(i,:),TSPAN);
matDerivEstadosPlant(i,:) = auxil';
end
dXTPlant = matDerivEstadosPlant(:,1);
dYTPlant = matDerivEstadosPlant(:,2);
dPSIPlant = matDerivEstadosPlant(:,3);
dvTPlant = matDerivEstadosPlant(:,4);
dALPHATPlant = matDerivEstadosPlant(:,5);
ddPSIPlant = matDerivEstadosPlant(:,6);
ddXPlant = dvTPlant.*cos(PSIPlant + ALPHATPlant) - vTPlant.*(dPSIPlant + dALPHATPlant).*sin(PSIPlant + ALPHATPlant);
ddYPlant = dvTPlant.*sin(PSIPlant + ALPHATPlant) + vTPlant.*(dPSIPlant + dALPHATPlant).*cos(PSIPlant + ALPHATPlant);
ACELNumPlant = [(ddXPlant.*cos(PSIPlant) - ddYPlant.*sin(PSIPlant)) (-ddXPlant.*sin(PSIPlant) + ddYPlant.*cos(PSIPlant))];
saidasModel = [XTModel YTModel PSIModel vTModel ALPHATModel dPSIModel];
matDerivEstadosModel = zeros(size(saidasModel));
for i = 1:size(saidasModel,1)
auxil = simulatorModel.Vehicle.Model(1,saidasModel(i,:),TSPAN);
matDerivEstadosModel(i,:) = auxil';
end
dXTModel = matDerivEstadosModel(:,1);
dYTModel = matDerivEstadosModel(:,2);
dPSIModel = matDerivEstadosModel(:,3);
dvTModel = matDerivEstadosModel(:,4);
dALPHATModel = matDerivEstadosModel(:,5);
ddPSIModel = matDerivEstadosModel(:,6);
ddXModel = dvTModel.*cos(PSIModel + ALPHATModel) - vTModel.*(dPSIModel + dALPHATModel).*sin(PSIModel + ALPHATModel);
ddYModel = dvTModel.*sin(PSIModel + ALPHATModel) + vTModel.*(dPSIModel + dALPHATModel).*cos(PSIModel + ALPHATModel);
ACELNumModel = [(ddXModel.*cos(PSIModel) - ddYModel.*sin(PSIModel)) (-ddXModel.*sin(PSIModel) + ddYModel.*cos(PSIModel))];
figure
ax = gca;
set(ax,'NextPlot','add','Box','on','XGrid','on','YGrid','on')
plot(TSPAN,ACELNumPlant(:,1),'r')
plot(TSPAN,ACELNumPlant(:,2),'g')
plot(TSPAN,ACELNumModel(:,1),'r--')
plot(TSPAN,ACELNumModel(:,2),'g--')
xlabel('time [s]')
ylabel('acc. [m/s]')
l = legend('AX Plant','AY Plant','AX Model','AY Model');
set(l,'Location','NorthEast')
%%
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]农思赢.铰接式车辆与俄军北极战役集群[J].坦克装甲车辆,2022(05):56-61.DOI:10.19486/j.cnki.11-1936/tj.2022.05.003.
[2]宋广昊. 铰接式车辆紧急变道避障控制策略研究[D].吉林大学,2021.DOI:10.27162/d.cnki.gjlin.2021.001808.
[3].采用DT-30PM铰接式车辆底盘的俄罗斯“雷神”M2DT防空导弹系统[J].坦克装甲车辆,2017(11):73.


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










