基于高频强调滤波的图像锐化

图像锐化作为图像处理中的关键技术，旨在增强图像中细节和边缘的清晰度，以提高图像的整体分辨率。图像锐化可以在空间域或频率域中实现。

空间域：常用方法为设定特定的卷积核，对图像进行卷积运算，突出图像的边缘细节特征。

频率域：常用的方法有高通滤波器、拉普拉斯算子等，通过将图像从空间域转换为频率域表示，并对其频率分量进行处理。

本文使用的图像锐化算法在频率域中进行，结合了高通滤波器与高频强调滤波算法实现图像锐化。

算法整体流程如下：

1、对图像进行傅里叶变换：由空间域转换为频率域。

2、使用高通滤波器过滤图像的低频部分。这里解释一下图像的频率形容了像素变化程度，也可以理解为相邻像素值梯度的变化强弱。所以低频部分代表了像素变化较为平坦的区域，高频部分代表像素变化较为强烈的区域，如噪声、边缘部分。因此高通滤波器的作用可以理解为提取图像的边缘特征。

3、使用高频强调滤波：将高通滤波器提取的边缘特征与原始图像进行加权融合，达到锐化的效果。

4、对图像进行逆傅里叶变换：由频率域转换回空间域。

代码如下：

创建好GaoTongLvBo.h头文件，使用时直接调用gaotong(const Mat f)函数即可，入参为待处理图像，输出为锐化后的图像。

#include <opencv2/opencv.hpp>  
#include <cmath>  
#include <complex>  
#include <iostream>  
#include "GaoTongLvBo.h"


using namespace cv;
using namespace std;
//将傅里叶变换后矩阵中的低频分量移动到中心
void manualShiftDFT(const Mat& complexI, Mat& complexI_shifted) {
    // 获取输入矩阵的大小  
    int M = complexI.rows;
    int N = complexI.cols;
    // 创建一个与输入相同大小的输出矩阵  
    complexI_shifted = Mat::zeros(complexI.size(), complexI.type());
    // 遍历输入矩阵的每个元素  
    for (int i = 0; i < M; i++) {
        for (int j = 0; j < N; j++) {
            int newRow = (i < M / 2) ? (i + M / 2) : (i - M / 2);
            int newCol = (j < N / 2) ? (j + N / 2) : (j - N / 2);
            complexI_shifted.at<Vec2d>(newRow, newCol) = complexI.at<Vec2d>(i, j);
        }
    }
}

//高通滤波实现
Mat gaotonglvbo(const Mat g_shifted, Mat one_minus_h,int M,int N) {

    // 应用高通滤波器  
    Mat result_highpass = Mat::zeros(g_shifted.size(), g_shifted.type());
    for (int i = 0; i < g_shifted.rows; i++) {
        for (int j = 0; j < g_shifted.cols; j++) {
            Vec2d g_val = g_shifted.at<Vec2d>(i, j);
            double h_val = one_minus_h.at<double>(i, j); // 注意：这里应该是单通道，但如果是复数则应该使用Vec2d  
            // 假设one_minus_h也是复数矩阵，如果是实数则需要相应调整  
            Vec2d result = Vec2d(g_val[0] * h_val, g_val[1] * h_val);
            result_highpass.at<Vec2d>(i, j) = result;
        }
    }
    return result_highpass;
}

//创建滤波器
Mat lvboqi(int M,int N) {
    // 定义高通滤波器的截止频率  
    double D0 = 40;
    // 创建滤波器  
    Mat H = Mat::zeros(M, N, CV_64F);
    for (int i = 0; i < M; i++) {
        for (int j = 0; j < N; j++) {
            double D = sqrt(pow(i - M / 2.0, 2) + pow(j - N / 2.0, 2));
            H.at<double>(i, j) = exp(-(D * D) / (2 * (D0 * D0)));
        }
    }
    return H;
}

//高通高频滤波整体算法
Mat gaotong(const Mat f) {
    int m = f.rows;
    int n = f.cols;
    int M1 = getOptimalDFTSize(f.rows);
    int N1 = getOptimalDFTSize(f.cols);
    Mat padded;
    copyMakeBorder(f, padded, 0, M1 - f.rows, 0, N1 - f.cols, BORDER_CONSTANT, Scalar::all(0));

    // 将图像转换为浮点型  
    Mat I;
    padded.convertTo(I, CV_64F);

    // 进行二维傅里叶变换  
    Mat g;
    dft(I, g, DFT_COMPLEX_OUTPUT);

    // 将零频率分量移到中心  
    Mat g_shifted;
    manualShiftDFT(g, g_shifted);
    // 获取矩阵尺寸  
    int M = g_shifted.rows;
    int N = g_shifted.cols;
    // 高通滤波与高频强调滤波结合，高频强调滤波  
    Mat F = Mat::zeros(M, N, CV_64F);
    F = 0.5 + 0.75 * (1 - lvboqi(M, N));

    Mat result_highpass2 = gaotonglvbo(g_shifted, F, M, N);

    // 将零频率分量移回原位  
    Mat G_shifted;
    manualShiftDFT(result_highpass2, G_shifted);

    // 进行逆傅里叶变换  
    Mat J2;
    idft(G_shifted, J2, DFT_SCALE | DFT_REAL_OUTPUT);
    // 提取原始大小的部分  
    cv::Mat J3 = J2(Rect(0, 0, n, m)); // 注意：Rect的宽和高参数是列数和行数


    // 取绝对值并转换为uint8  
    Mat J4;
    magnitude(J3.rowRange(0, J3.rows).colRange(0, J3.cols),
        Mat::zeros(J3.rows, J3.cols, J3.type()), J4); // 注意：magnitude需要两个输入矩阵  
    J4.convertTo(J4, CV_8U);


    return J4;
}

锐化效果：

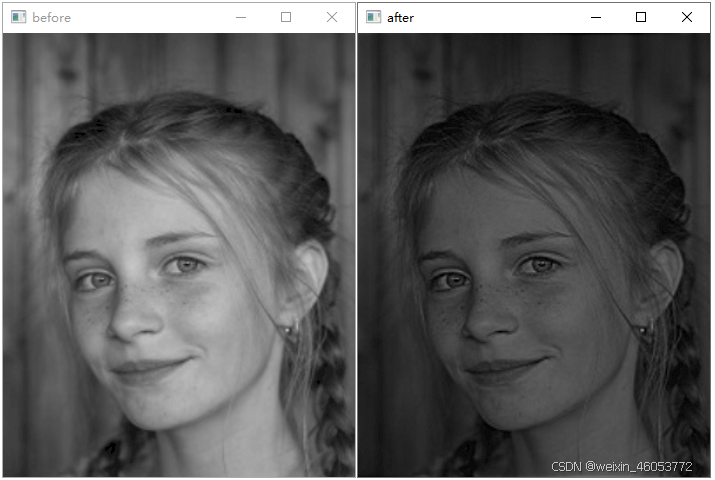
可以看出图像的边缘细节信息得到有效增强，处理后的图像变暗，可以结合自适应直方图均衡化算法进行对比度增强。