基础博弈

P2197 【模板】nim游戏

必胜状态和必败状态：
在解决这个问题之前，先来了解两个名词：
  必胜状态，先手进行某一个操作，留给后手是一个必败状态时，对于先手来说是一个必胜状态。即先手可以走到某一个必败状态。
  必败状态，先手无论如何操作，留给后手都是一个必胜状态时，对于先手来说是一个必败状态。即先手走不到任何一个必败状态。
  结论：假设n堆石子，石子数目分别是a1,a2,…,an，如果a1⊕a2⊕…⊕an≠0，先手必胜；否则先手必败。
  操作到最后时，每堆石子数都是0，0⊕0⊕…0=0，在操作过程中，如果 a1⊕a2⊕…⊕an=x≠0。那么玩家必然可以通过拿走某一堆若干个石子将异或结果变为0。
  证明：不妨设x的二进制表示中最高一位1在第k位，那么在a1,a2,…,an中，必然有一个数ai，它的第k为时1，且ai⊕x<ai，那么从第i堆石子中拿走(ai−ai⊕x)个石子，第i堆石子还剩ai−(ai−ai⊕x)=ai⊕x，此时a1⊕a2⊕…⊕ai⊕x⊕…⊕an=x⊕x=0。
  在操作过程中，如果 a1⊕a2⊕…⊕an=0，那么无论玩家怎么拿，必然会导致最终异或结果不为0。
  反证法：假设玩家从第ii堆石子拿走若干个，结果仍是0。不妨设还剩下a′个，因为不能不拿，所以0≤a′<ai，且a1⊕a2⊕…⊕a′⊕…⊕an=0。那么(a1⊕a2⊕…⊕ai⊕…an)⊕(a1⊕a2⊕…⊕a′⊕…⊕an)=ai⊕a′=0，则 ai=a′，与假设0≤a′<ai矛盾。
  基于上述三个证明：1. 如果先手面对的局面是a1⊕a2⊕…⊕an≠0，那么先手总可以通过拿走某一堆若干个石子，将局面变成a1⊕a2⊕…⊕an=0。如此重复，最后一定是后手面临最终没有石子可拿的状态。先手必胜。2. 如果先手面对的局面是a1⊕a2⊕…⊕an=0，那么无论先手怎么拿，都会将局面变成a1⊕a2⊕…⊕an≠0，那么后手总可以通过拿走某一堆若干个石子，将局面变成a1⊕a2⊕…⊕an=0。如此重复，最后一定是先手面临最终没有石子可拿的状态。先手必败。
具体的实现代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

void debug_out(){
   
    cerr << endl;
}
template<typename Head, typename... Tail>
void debug_out(Head H, Tail... T){
   
    cerr << " " << to_string(H);
    debug_out(T...);
}
#ifdef local
#define debug(...) cerr<<"["<<#__VA_ARGS__<<"]:",debug_out(__VA_ARGS__)
#else
#define debug(...) 55
#endif
int main(){
   
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	int n, x, ans = 0; 
	cin >> n;
	for(int i = 1; i <= n; i++){
   
		cin >> x;
		ans ^= x;
	}
	if(ans) cout << "Yes\n";
	else cout << "No\n";
	return 0; 
} 

AcWing 892. 台阶-Nim游戏

  此时我们需要将奇数台阶看做一个经典的Nim游戏，如果先手时奇数台阶上的值的异或值为0，则先手必败，反之必胜。
  证明：先手时，如果奇数台阶异或非0，根据经典Nim游戏，先手总有一种方式使奇数台阶异或为0，于是先手留了技术台阶异或为0的状态给后手
  于是轮到后手：①当后手移动偶数台阶上的石子时，先手只需将对手移动的石子继续移到下一个台阶，这样奇数台阶的石子相当于没变，于是留给后手的又是奇数台阶异或为0的状态②当后手移动奇数台阶上的石子时，留给先手的奇数台阶异或非0，根据经典Nim游戏，先手总能找出一种方案使奇数台阶异或为0
  因此无论后手如何移动，先手总能通过操作把奇数异或为0的情况留给后手，当奇数台阶全为0时，只留下偶数台阶上有石子。（核心就是：先手总是把奇数台阶异或为0的状态留给对面，即总是将必败态交给对面）
  因为偶数台阶上的石子要想移动到地面，必然需要经过偶数次移动，又因为奇数台阶全0的情况是留给后手的，因此先手总是可以将石子移动到地面，当将最后一个（堆）石子移动到地面时，后手无法操作，即后手失败。
  因此如果先手时奇数台阶上的值的异或值为非0，则先手必胜，反之必败！
具体的实现代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

void debug_out(){
   
    cerr << endl;
}
template<typename Head, typename... Tail>
void debug_out(Head H, Tail... T){
   
    cerr << " " << to_string(H);
    debug_out(T...);
}
#ifdef local
#define debug(...) cerr<<"["<<#__VA_ARGS__<<"]:",debug_out(__VA_ARGS__)
#else
#define debug(...) 55
#endif
int main(){
   
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	int n, x, ans = 0; 
	cin >> n;
	for(int i = 1; i <= n; i++){
   
		cin >> x;
		if(i % 2) ans ^= x;
	}
	if(ans) cout << "Yes\n";
	else cout << "No\n";
	return 0; 
} 

AcWing 893. 集合-Nim游戏

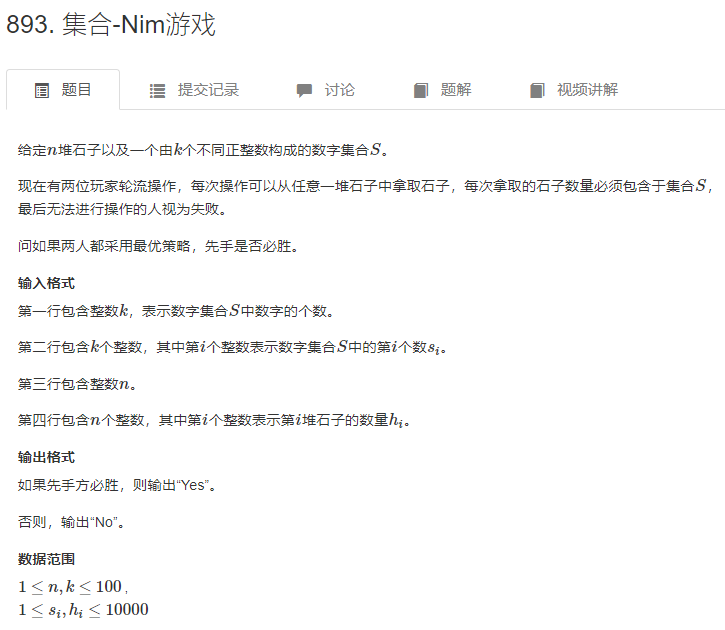
先介绍下SG函数：
（网上的图，挺详细的！）


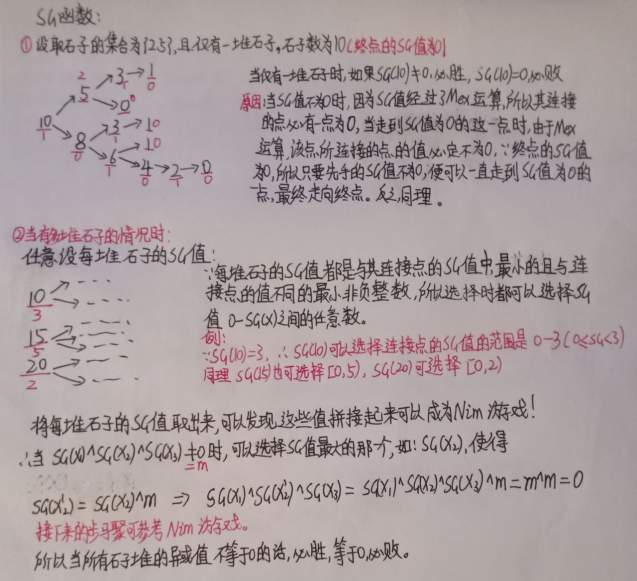
1.Mex运算：
  设S表示一个非负整数集合.定义mex(S)为求出不属于集合S的最小非负整数运算,即:mes(S)=min{x};例如:S={0,1,2,4},那么mes(S)=3;
2.SG函数：
  在有向图游戏中,对于每个节点x,设从x出发共有k条有向边,分别到达节点y1,y2,……yk,定义SG(x)的后记节点y1,y2,……yk的SG函数值构成的集合在执行mex运算的结果,即:SG(x)=mex({SG(y1),SG(y2)····SG(yk)})
  特别地,整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值,即 SG(G)=SG(s)。
3.有向图游戏的和：
  设G1，G2,……,Gm是m个有向图游戏.定义有向图游戏G,他的行动规则是任选某个有向图游戏Gi,并在Gi上行动一步.G被称为有向图游戏G1,G2,……,Gm的和.
  有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数的异或和,即:SG(G)=SG(G1)xorSG(G2)xor···xor SG(Gm)
具体的代码实现：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

void debug_out(){
   
    cerr << endl;
}
template<typename Head, typename... Tail>
void debug_out(Head H, Tail... T){
   
    cerr << " " << to_string(H);
    debug_out(T...);
}
#ifdef local
#define debug(...) cerr<<"["<<#__VA_ARGS__<<"]:",debug_out(__VA_ARGS__)
#else
#define debug(...) 55
#endif
const int N = 105, M = 10005;
int s[N], f[M], n, m;
int sg(int x){
   
	if(f[x] != -1) return f[x];
	unordered_set<int> S;
	for(int i = 1; i <= n; i++){
   
		if(x >= s[i]) S.insert(sg(x - s[i]));
	}
	for(int i = 0; ; i++){
   
		if(!S.count(i)) return f[x] = i;
	}
}
int main(){
   
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	int x, ans = 0;
	cin >> n;
	for(int i = 1; i <= n; i++){
   
		cin >> s[i];
	}
	cin >> m;
	memset(f, -1, sizeof(f));
	while(m--){
   
		cin >> x;
		ans ^= sg(x);
	}
	if(ans) cout << "Yes\n";
	else cout << "No\n";  
	return 0; 
} 

AcWing 894. 拆分-Nim游戏

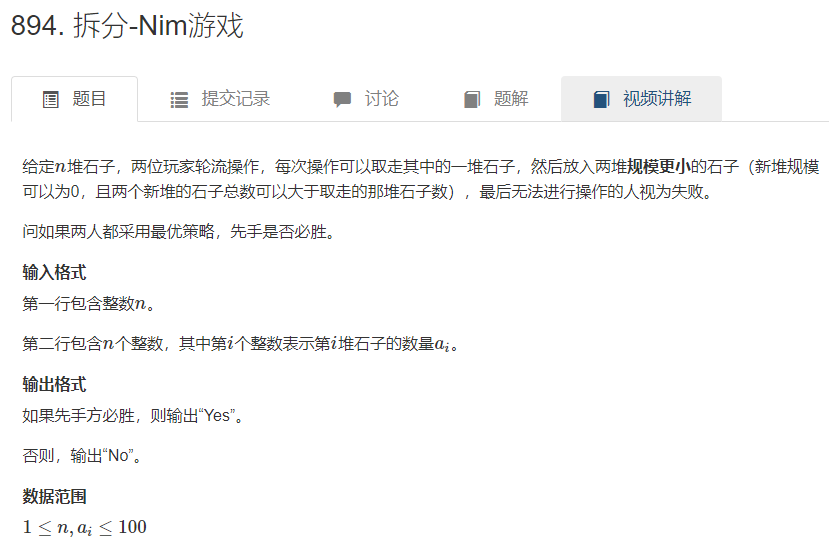
  相比于集合-Nim，这里的每一堆可以变成不大于原来那堆的任意大小的两堆
  即a[i]可以拆分成(b[i],b[j]),为了避免重复规定b[i]>=b[j],即：a[i]>=b[i]>=b[j]
  相当于一个局面拆分成了两个局面，由SG函数理论，多个独立局面的SG值，等于这些局面SG值的异或和。
  因此需要存储的状态就是sg(b[i])^sg(b[j])（与集合-Nim的唯一区别）
具体的代码实现：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

void debug_out(){
   
    cerr << endl;
}
template<typename Head, typename... Tail>
void debug_out(Head H, Tail... T){
   
    cerr << " " << to_string(H);
    debug_out(T...);
}
#ifdef local
#define debug(...) cerr<<"["<<#__VA_ARGS__<<"]:",debug_out(__VA_ARGS__)
#else
#define debug(...) 55
#endif
const int N = 105;
int f[N];
int sg(int x){
   
	if(f[x] != -1) return f[x];
	unordered_set<int> S;
	for(int i = 0; i < x; i++){
   
		for(int j = 0; j<= i; j++){
   
			S.insert(sg(i) ^ sg(j));
		}
	}
	for(int i = 0; ; i++){
   
		if(!S.count(i