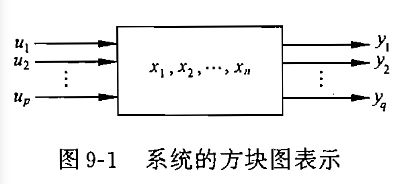
系统数学描述的两种基本类型
①外部描述(不完全)——输入输出描述(u和y的关系式)
②内部描述(完全)——状态空间描述——由状态方程(表征x和u关系的微分方程或差分方程)和输出方程(表征x及u和y关系的代数方程)
系统描述中的常用基本概念
①输入和输出
②松弛性——系统在t0时刻之后的输出由t0时刻后的输入唯一确定,则称系统在t0时刻是松弛的,松弛系统y=Hu
③因果性(或因果关系)——系统在t时刻的输出仅取决于t时刻和t之前的输入
④线性——满足叠加原理
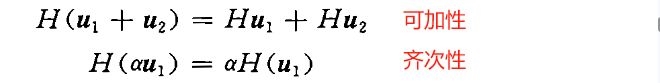
⑤时不变性(定常性)——HQαu=QαHu或HQαu=Qαy,Qau(t)=u(t-α)
系统状态空间描述的常用基本概念
①状态和状态变量——x1(t),x2(t),...,xn(t)
②状态向量
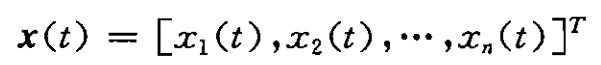
③状态空间
④状态轨线
⑤状态方程
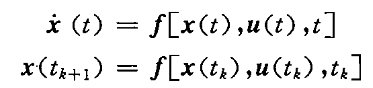
⑥输出方程
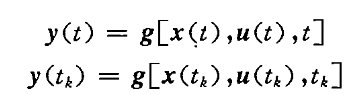
⑦状态空间方程
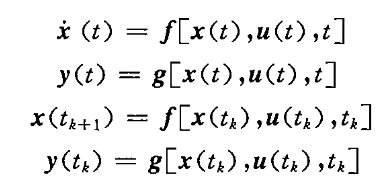
⑧自治系统
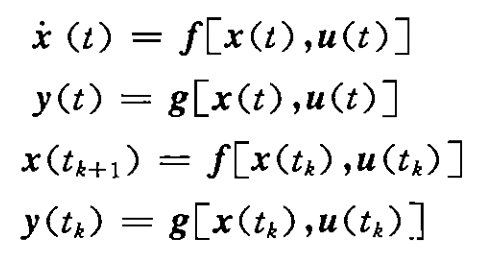
⑨线性系统
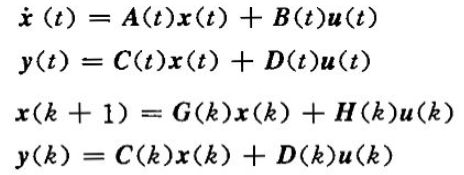
当D恒等于0时,系统称为绝对固有系统,否则称为固有系统,可以简记为系统(A,B,C,D)或系统(G,H,C,D);相应的绝对固有系统为系统(A,B,C)或系统(G,H,C)
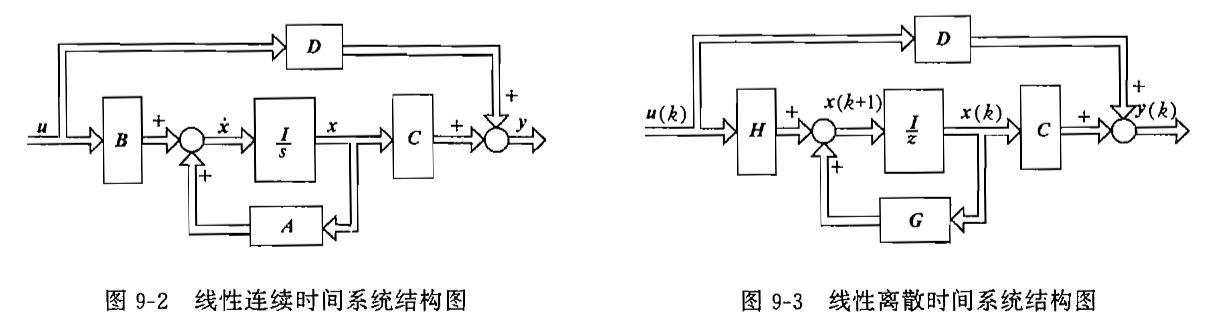
⑩状态空间分析法
线性定常连续系统的状态空间表达式的建立
①根据系统的机理建立相应的微分方程或差分方程,继而选择有关的物理量作为状态变量,从而导出其状态空间表达式
②由已知的系统其他数学模型经过转化而得到状态空间表达式
(1)系统输入量中不含导数项
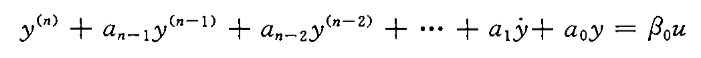
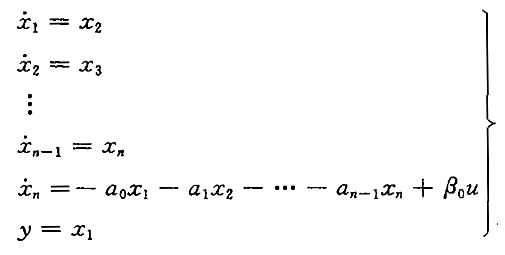
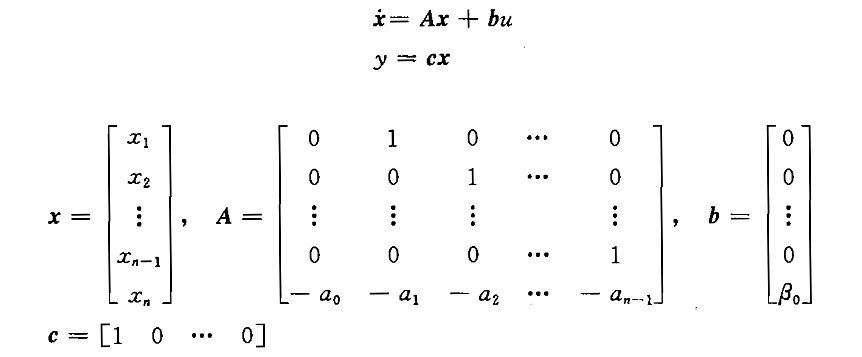
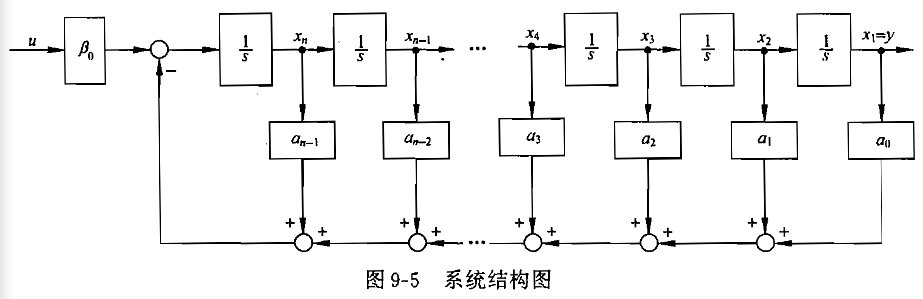
(2)系统输入量中含有导数项
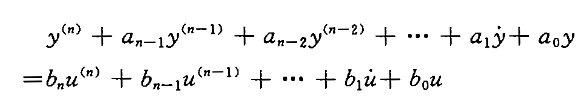
令
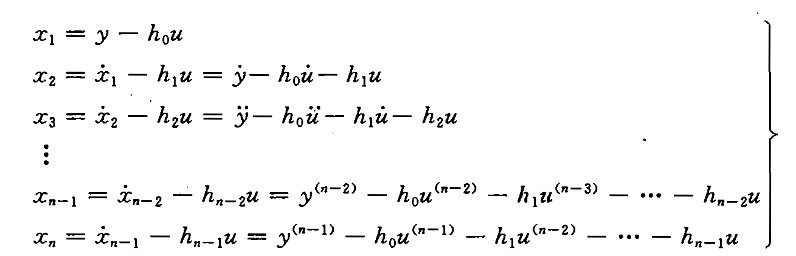
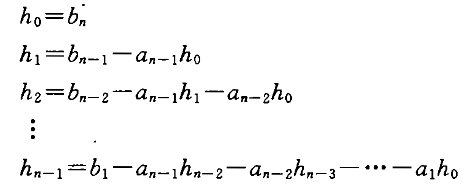
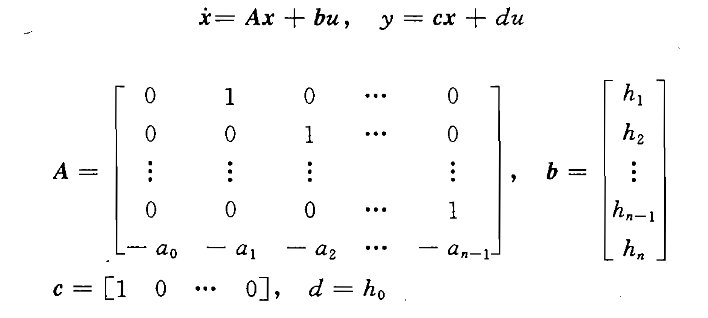
或者令
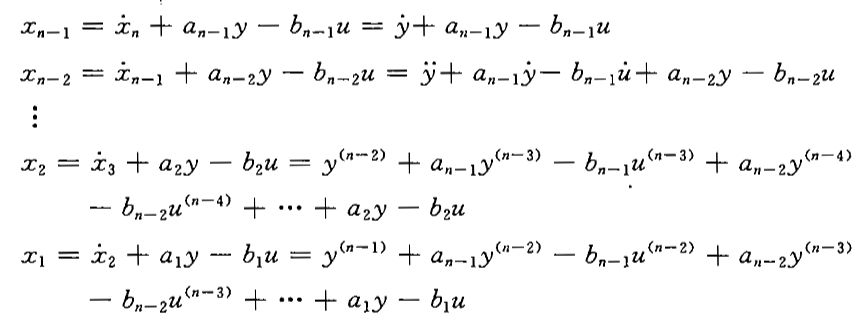
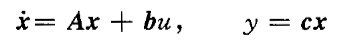
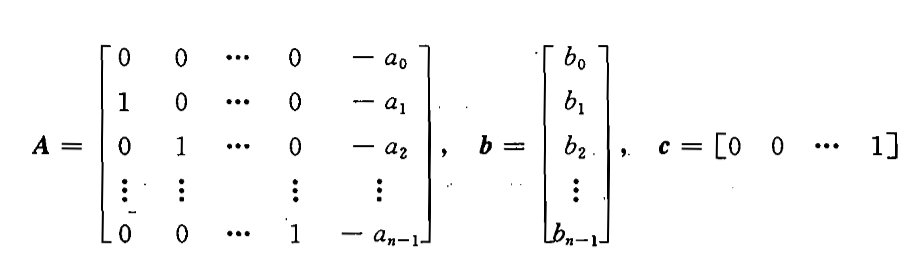
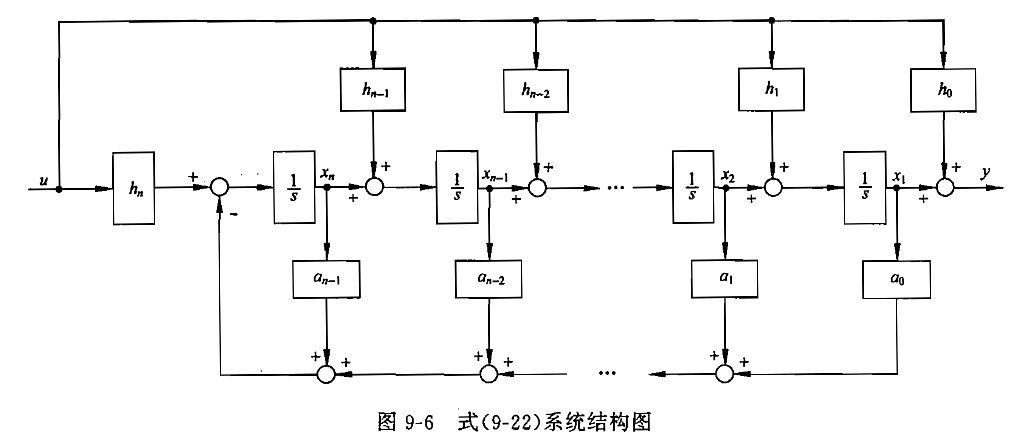
③由系统传递函数建立状态空间表达式
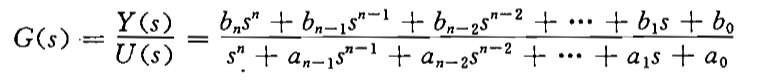
应用综合除法,得
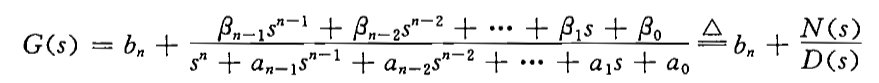
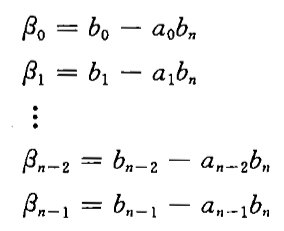
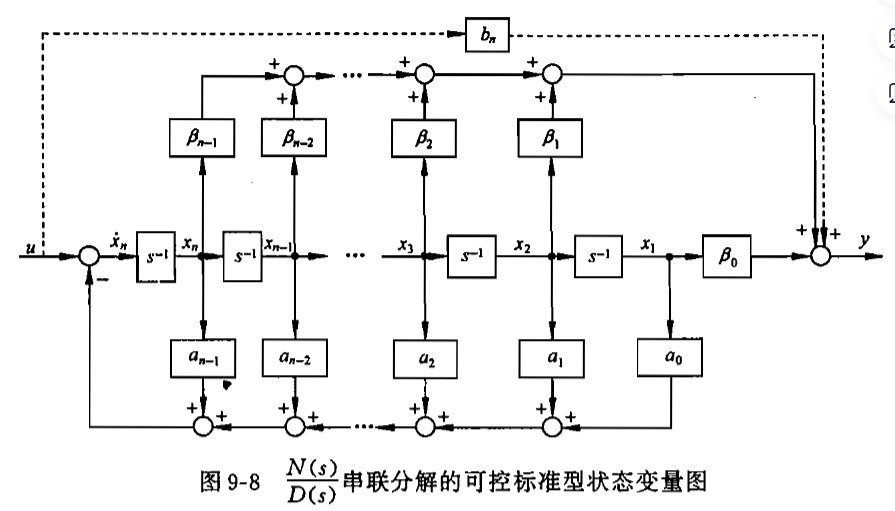
(1)串联分解
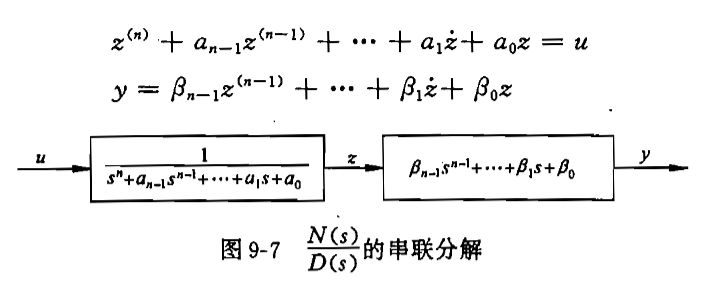

A称为友矩阵,状态方程中的A,b有这种形式,则称为可控标准型
当β1=β2=...=βn-1=0时,A,b不变,c=[β0 0 ... 0]
当bn=0时,
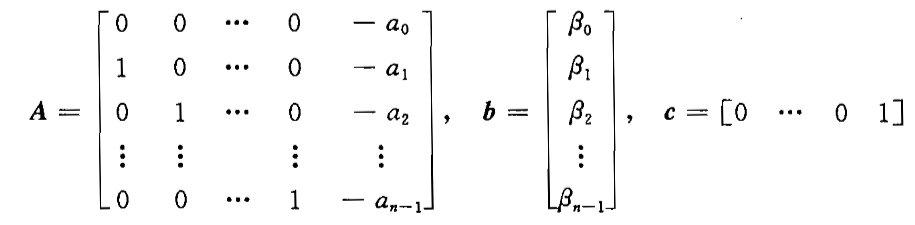
A为友矩阵的转置,状态方程中A,b有这种形式,则称为可观测标准型
下标c表示可控标准型,下标o表示可观测标准型,则有

(2)只含单实极点
可化为对角型动态方程,A是一个对角矩阵

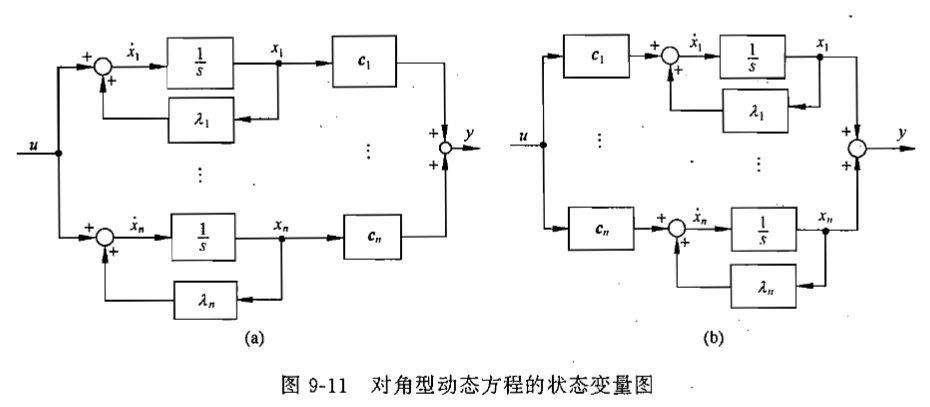
(a)

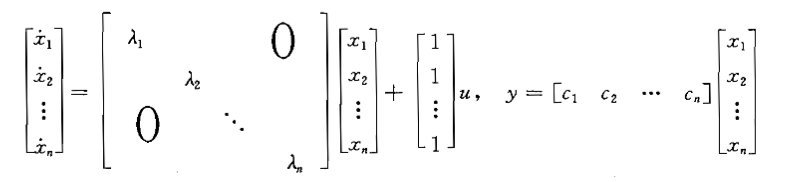
(b)

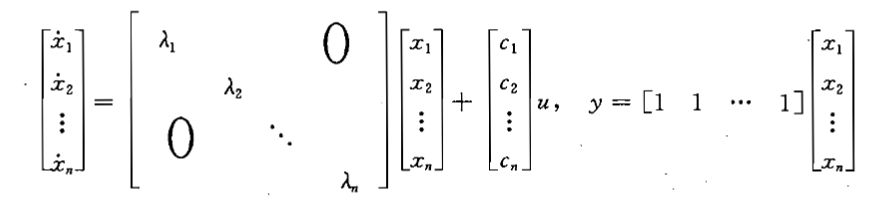
(a)(b)存在对偶关系
(3)含重实极点时的情况

(a)
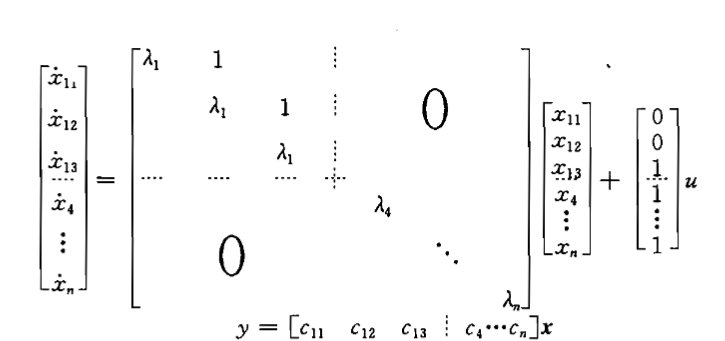
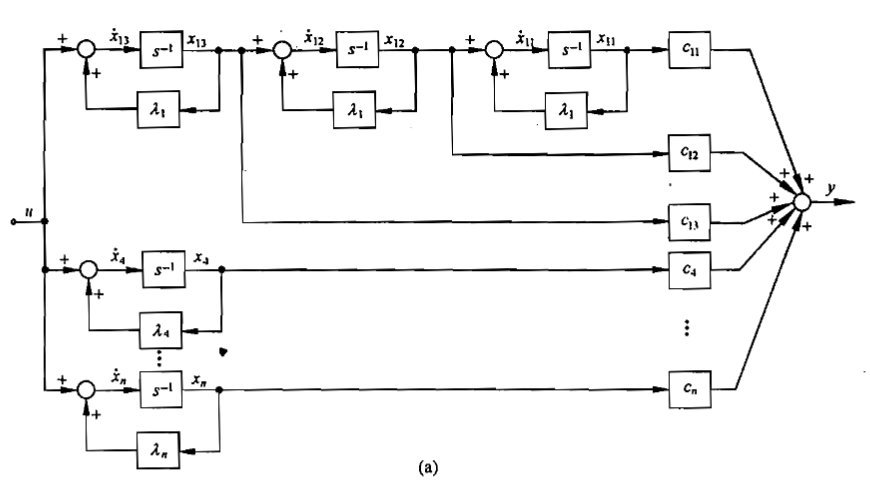
(b)
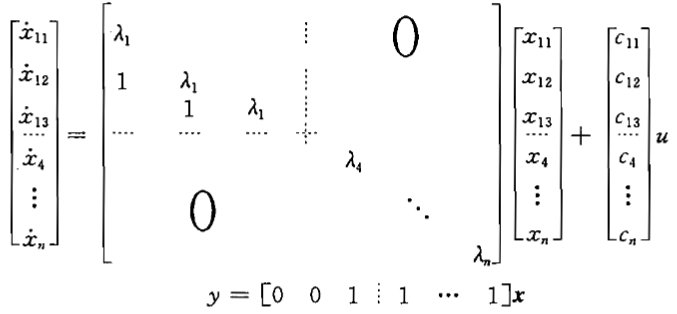
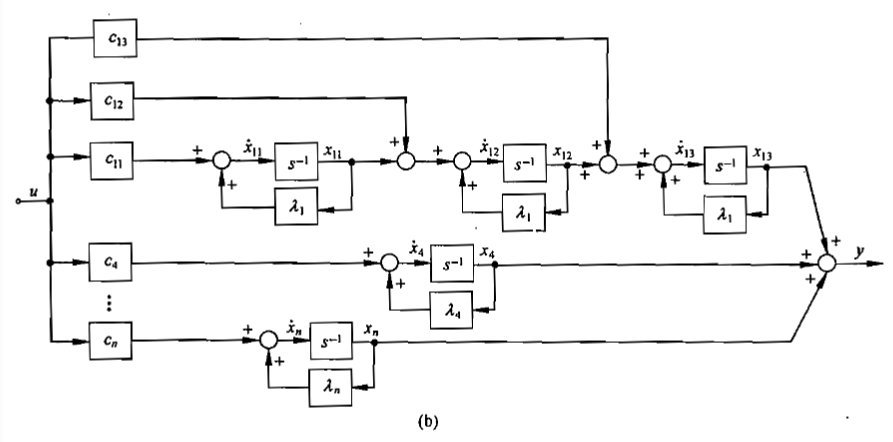
(a)(b)称为约当型,存在对偶关系
线性定常连续系统状态方程的解
①齐次状态方程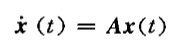
(1)幂级数法
设解为


(2)拉普拉斯变换法
取拉氏变换,得
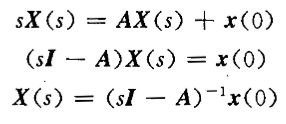
取拉氏反变换,得
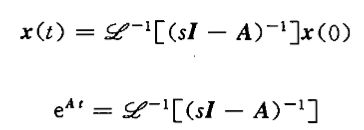
所以,求解齐次状态方程,就是计算状态转移矩阵Ф(t)
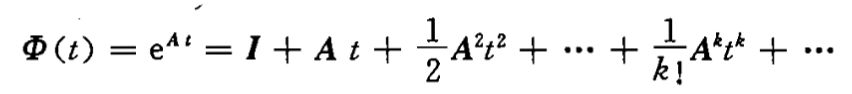
运算性质
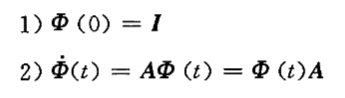








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 89
89

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








