【六更完结！由于字数限制开新文章继续】零基础信号与系统学习笔记：复指数信号、傅里叶级数的系数推导、三角函数正交性、离散傅里叶变换、相位补偿、z变换表、逆变换表、常见序列及其作用

终于还是躲不过信号与系统，在此记录学习笔记。😉 争取从零开始一遍搞懂
定期更新！！！【2020年4月14日完结】

友链：奥本海姆第三章

基础1：复指数信号

复指数信号基础知识

• 复指数信号是指数信号的指数因子是复数时，称之为复指数信号。
• 复指数信号在物理上是不可实现的，但是它概括了多种情况。利用复指数信号可以表示常见的普通信号，如直流信号、指数信号、正弦信号等。
• 复指数信号的微分和积分仍然是复指数信号，利用复指数信号可以使许多运算和分析简化。因此，复指数信号是信号分析中非常重要的基本信号。

复指数信号推导1

一般情况下的复指数信号为$f(x)=K{e}^{(\sigma +jw)t}$，其中$\sigma$表示实部，w表示虚部，K是实数，记复数$s=\sigma +jw$，则$f(x)=K{e}^{st}$。
借助欧拉公式展开：

$f(x)=K{e}^{(\sigma +jw)t}=K{e}^{\sigma t+jwt}=K{e}^{\sigma t}(cos(wt)+jsin(wt))$

此结果表明：

• 一个复指数信号可分为实、虚两部分。
• 实部包含余弦信号，虚部则为正弦信号。指数因子实部$\sigma$表表示振幅随时间变化的情况.
• 指数因子的虚部w表示角频率

相应的，结题技巧有：
$$\cos (n\cos t)=\frac{1}{2}\left(e^{j{w}_{0}t}+e^{-j{w}_{0}t}\right)$$

虚指数信号

当振幅不随时间变化时，$\sigma =0$，则信号是$e^{jwt}$，称为虚指数信号。

• 虚指数信号形式，为等幅正弦信号。
• 具有周期性，其周期为2π/ω；

虚指数信号特性和作用

$|e^{jwt}|=co{s}^2(wt)+si{n}^2(wt)=1$，即一个周期复指数信号$e^{jwt}$的绝对值的平方等于1。

如果把虚指数信号作为控制系统的输入函数，那么系统的输出也应当是一个复数，输出的实部与输入的实部：cos（wt）相对应；输出的虚部与输入的虚部：sin(wt)相对应。

作用：
输入一个复指数函数，输出也是复指数，此时可以计算系统输出的振幅($\sqrt{(响应实{部}^2+响应虚{部}^2)}$)和相位$w$。

直流信号

当$\sigma =0且w=0$时，即s=0，此时信号退化为直流信号。

基础2：傅里叶级数

任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示，这个级数就称为傅里叶级数
$$\boxed{\begin{array}{rl}X(t)=& a_0+\sum _{n=1}^{\infty }\left[a_n\cos (n\omega t)+b_n\sin (n\omega t)\right]=\\ & a_0+\sum _{n=1}^{\infty }{c}_n\sin \left(n\omega t+{\theta }_n\right)=\\ & a_0+c_1\sin \left(\omega t+{\theta }_1\right)+c_2\sin \left(2\omega t+{\theta }_2\right)+\cdots \\ & n=1,2,\cdots \end{array}}$$
特别注意：X(t)周期是T，则cos, sin 的周期是T/n

推导傅里叶级数的系数

使用基础1中的虚指数信号，得到
$$\boxed{X(t)=\sum _{k=-\infty }^{+\infty }{a}_k\cdot e^{jk{w}_{0}t}}$$

左右同乘$e^{-jn{\omega }_{0}t}$得到：
$$x(t)e^{-jn{\omega }_{0}t}=\sum _{k=-\infty }^{+\infty }{a}_k{e}^{j(k-n){\omega }_{0}t}$$

两边对t从0到$T=2\pi /w_0$积分：
$${\int }_0^{T}x(t)e^{-jn{\omega }_{0}t}dt={\int }_0^T\sum _{k=-\infty }^{+\infty }{a}_k{e}^{j(k-n){\omega }_{0}t}dt$$
调换积分次序，提取$a_k$：
$${\int }_0^{T}x(t)e^{-jn{\omega }_{0}t}dt=\sum _{k=-\infty }^{+\infty }{a}_k\left[{\int }_0^T{e}^{j(k-n){\omega }_{0}t}dt\right]$$

对于右边的积分，由欧拉关系：
$${\int }_0^T{e}^{j(k-n){\omega }_{0}t}dt={\int }_0^T\cos (k-n){\omega }_{0}tdt+j{\int }_0^T\sin (k-n){\omega }_{0}tdt$$
由三角函数积分的正交性*(见扩充知识)，积分值当且仅当n=k时不为0：
$$\begin{array}{rl}& \sum _{k=-\infty }^{+\infty }{a}_k\left[{\int }_0^T{e}^{j(k-n){\omega }_{0}t}dt\right]=T{a}_n\\ & a_n=\frac{1}{T}{\int }_0^{T}x(t)e^{-jn{\omega }_{0}t}dt\end{array}$$

即知傅里叶级数的系数为
$$\boxed{a_n=\frac{1}{T}{\int }_0^{T}x(t)e^{-jn{\omega }_{0}t}dt}$$

扩充知识1：三角函数正交性

“建立三角函数坐标系，1，coswt,cos2wt,…,sinwt,sin2wt,…为正交基（不同基点积=0，同基点积！=1，所以是正交基，但是非标准正交基），则函数f(t)可以表示为三角函数坐标系下的点，其坐标即为a0,an,bn。用f(t)与各个基进行点积计算就可得到a0,an,bn”
该段参考：https://blog.csdn.net/lijil168/article/details/89261861

例题：已知$f(t)=a_0+{\sum }_{n=1}^{\infty }\left(a_n\cos nwt+b_n\sin wt\right)$，求解$a_0、a_n、b_n$
解：

• 点积$⟨u,v⟩$：等价于按点乘累加，$⟨u,v⟩=\int uvdt$
  

$$a_0=\frac{⟨f,1⟩}{⟨1,1⟩}=\frac{{\int }_{-\frac{1}{2}}^{\frac{T}{2}}f(t)dt}{{\int }_{-\frac{1}{2}}^{\frac{T}{2}}dt}=\frac{{\int }_{-\frac{T}{2}}^{\frac{T}{2}}f(t)dt}{T}$$
$$a_n=\frac{⟨f,\cos nwt⟩}{⟨\cos nt,\text{ cosn }wt⟩}=\frac{{\int }_{-\frac{\pi }{2}}^{\frac{T}{2}}f(t)\cos ntdt}{{\int }_{-\frac{T}{2}}^{\frac{T}{2}}{\cos }^{2}nwtdt}=\frac{{\int }_{-\frac{T}{2}}^{\frac{T}{2}}f(t)\cos nwtdt}{\frac{T}{2}}$$
$$b_n=\frac{⟨f,\sin nwt⟩}{⟨\sin nwt,\sin nwt⟩}=\frac{{\int }_{-\frac{1}{2}}^{\frac{\pi }{2}}f(t)\sin nwtdt}{{\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}{\sin }^{2}nvtdt}=\frac{{\int }_{-\frac{\pi }{2}}^{\frac{\pi }{2}}f(t)\sin nwtdt}{\frac{T}{2}}$$

注意：三角基正交，但不是标准正交基，因为$⟨1,1⟩，⟨cosnwt,cosnwt⟩，⟨sinnwt,sinnwt⟩\ne 1$

三角函数第二积分常用公式

$$\boxed{{\int }_0^{\frac{x}{2}}{\cos }^{n}xdx={\int }_0^{\frac{\pi }{2}}{\sin }^{n}xdx=\{\begin{array}{ll}\frac{(2m-1)!!}{(2m)!!}\cdot \frac{\pi }{2}& n=2m\\ \frac{(2m-2)!!}{(2m-1)!!},& n=2m-1\end{array}}$$

基础三：常见序列的作用

以下内容摘自奥本海姆-离散时间信号处理

单位样本序列$\delta$[n]

单位阶跃序列u[n]

---

二更：
加油冲。

李永乐老师笔记

时域和频域是在不同角度观察信号：

由于现实中存在着大量信号是非周期的信号，可以看成周期是无穷。
利用上文提到的三角函数正交性，只需要内积，也就是上文的傅里叶变换公式，就可以提取包含$w$的成分（如果不包含，则内积结果为0）

拉普拉斯变换和衰减因子

因为所有的正弦波余弦波都有最大值，如果要描述一个在远处是无穷的信号，就很没用。因此要对原信号乘上一个衰减因子。
在上文进行展开时我们用到了:
$f(x)=K{e}^{(\sigma +jw)t}=K{e}^{\sigma t+jwt}=K{e}^{\sigma t}(cos(wt)+jsin(wt))$
这里的$\sigma$就可以看做一种衰减因子（<0时）

有衰减因子的傅里叶变换：
$${\int }_{-\infty }^{+\infty }f(t)e^{-\sigma t}\cdot e^{-jwt}\cdot dt$$

物理上还可以理解为：为让一个边震荡边增加幅度的正弦波来参与原函数。

离散傅里叶变换

在上文中已经推导了函数的傅里叶系数，则对于周期为2$\pi$的周期函数$f(x)$，且$f(x)=\frac{a_0}{2}+{\sum }_{n=1}^{\infty }\left(a_n\cos nx+b_n\sin nx\right)$有：
$$\begin{array}{rl}f(x)& =\frac{a_0}{2}+\sum _{n=1}^{\infty }\left(a_n\cos nx+b_n\sin nx\right)\\ (a_n& =\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)\cos nx\mathrm{d}x(n=0,1,\cdots )\\ b_n& =\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)\sin nx\mathrm{d}x(n=1,2,\cdots )\end{array}$$
第一行称为傅里叶级数，第二行第三行称为傅里叶系数。

离散形式和补偿规律

参考https://www.zhihu.com/question/279808864/answer/552617806
希望得到(0,1,0,0)的离散信号【周期为4，在时间点time=2时输出1，time=1,3,4输出0】，则需要先获得(1,0,0,0)，然后移位，即对相位进行补偿，从而获得移位的效果。

利用：

• 当两个单位圆周（单位值号）之间角度差180度的时
  候，他俩相加所得的信号振幅为0。
• 三个单位圆周角度互相相差120度时，也有同样现象。
• … …
• n个单位圆周角度互相差360/n度时，信号振幅和为0

即可获得单位圆震荡的表示方法，动图见上文知乎链接。

使用虚指数信号的话，即可表示成：从$e^{-i2\pi \frac{0}{4}}$补偿到$e^{-i2\pi \frac{1}{4}}$，即可实现(0,1,0,0)

图像高低频率性质

以照片为例，低频表示人的轮廓，高频表示人的细节（如斑点，皱纹等）
磨皮一定程度上就是去掉高频成分

相位补偿

更长的信号可以通过叠加$e^{-i2\pi \frac{i}{k}}$的方式，对时间点有k个的单位信号补偿$i$。

对于不同频率信号来说，圆周的旋转素履是不同的。我们的信号周期为4,频率为1Hz, 时移1需要1/4*360=90度的相位补偿，同理1Hz信号时移2,或者2Hz的信号时移1,都需要180度。
公式：$2\pi \frac{n-1}{N}$

而当信号是(m_{1},m_{2},m_{3},m_{4})类型的时候，$e^{-i2\pi \frac{i}{k}}$前还需要乘以幅值平均$m_i/4$

对于某特定频率k，即可得到离散傅里叶变换公式：
$$X_k=\frac{1}{N}\sum _{n=0}^{N-1}{x}_n\cdot e^{-\frac{2\pi i}{N}kn}$$
形象化解释：

傅里叶变换后周期的改变情况：

周期<—>离散，非周期<—>连续

---

三更：

Z变换

基础知识：洛伦级数

洛朗级数是泰勒级数的延拓版
参考：https://www.zhihu.com/question/26482591
阿贝尔定理：

泰勒：


洛伦：

z变换和拉普拉斯变换的关系

参考https://www.bilibili.com/video/BV1TW411F7wj?from=search&seid=15474440315054549
z变换相当于一个封装了更多的拉普拉斯变换
$$\begin{array}{rl}z& =e^{(\sigma +jw)T}\\ & =e^{\sigma \cdot T}\cdot e^{jw\cdot T}\\ & =A\cdot e^{j\phi }\end{array}$$
z就相当于一根长A，角$j\phi$的棍子

$\sigma =0$时，拉普拉斯变换退化成傅里叶变换
$$\sigma =0⟶S=\sigma +jw=jw$$
此时A=1，所以傅里叶变换是单位圆上的z变换。

z变换可以由离散信号的拉普拉斯变换推导过来：

左式$F_s(s)$中，_{s}表示sample, (s)表示复数s
右式T是指0和1之间的间隔。
立体上来看：

带上${}^n$之后就相当于敲碎成一个一个离散的点
（二维视图）

没有${}^n$就是单独一个点：
$$\begin{array}{l}{e}^{sT}\\ =e^{(\sigma +j\omega )T}\\ =e^{{\sigma }_T}\cdot e^{j{w}_T}\\ =A\cdot \left(coswT+j\sin wT\right)\\ =A(a+bj)\end{array}$$
四更继续z变换
参考中国大学慕课-东南大学数字信号处理

---

学术定义算子和收敛域

奥本海姆定义：

网课定义：

单边z变换只对大于等于0作变换

但如果只给出表达式，不给出收敛域，是很不对的
对于一个相同的z变换，给定不同的收敛域，那反应的序列也不一样。
一般收敛域是一个圆环


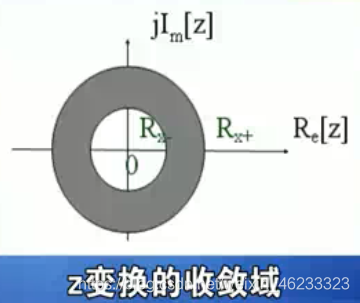
下面讨论三种不同序列的收敛域：

1 ：有限长序列

这个序列因为是有限的，只要项里没有无穷，则在几乎整个z平面上收敛，

注意：需要单独讨论0点和无穷点。

经常能满足一个条件，所以要么包含零点，要么包含零点

只有一个特例序列，两边都包含，就是下图：

例子2：
矩形序列x(n)=$R_N(n)$，收敛域是0到N-1

$$X(z)=\sum _{n=-\infty }^{\infty }{R}_N(n)z^{-n}=\sum _{n=0}^{N-1}{z}^{-n}=1+z^{-1}+z^{-2}-1+\cdots +z^{-(N-1)}$$
$$X(z)=\frac{1-z^{-N}}{1-z^{-1}},0<1z|\le \infty$$

2: 右边序列

收敛域在圆外，包含了无穷远点。

3：左边序列

4: 双边序列

可以看做两者之和

可以分解后分别求

收敛域是公共部分的圆环

z变换小结

z变换作用和特点

z变换例题

逆z变换

c在收敛区间内

在收敛圆环上做围线积分

因为围线积分很麻烦，求解逆z变换有三种方法

• 幂级数
• 留数定理
• 部分分式

正变换和收敛域重要，逆变换用的不多

z变换表和逆变换计算方法

部分分式，写成零点-极点式子

特别强调

对x(n-n0)做z变换：
$$\boxed{Z(X(n-n_0))=Z^{-n0}X(z)}$$
其中右式X(z)表示对X(n)做z变换

所以看到z的负幂次，实际实现的是系统的延迟

常用序列的z变换

记住：
（$R_N(n)$在z->无穷时和u（n）相同）

【现在已经写了一万三千字了。。真不容易啊，您能看到这个地方也不容易】

【重要性质】Parseval 定理

【所有正交变换都满足该定理，后面DFT也会遇到】
本质上反映能量相同

离散时间系统

八位系统即可完成的A/D转换：数码相机（每个颜色8位）
24位：声卡【HD-CD就达到24w位】
12位：打电话的采样
采用不同采样精度的原因：钱。

一般把系统认为黑盒子，只研究输入输出的关系，不考虑实现：

最常用：线性时不变系统，本课将主要研究此处

采样频率

z变换是DTFT的一般化，在系统里很有用。反映了频谱关系。
目前DTFT：频域上连续
DFT：频域上离散

离散化之后就不用积分了。
DFT延伸出FFT（更快计算）

字数太多老出BUG,本文就此完结。开新文章讲离散时间系统。

【感谢您阅读到这里的毅力】