资料
参考视频:
【详细推导】【本视频还证明了收敛性】https://www.bilibili.com/video/BV16a4y1t76z?from=search&seid=35153938940534319
【简单介绍】https://www.bilibili.com/video/BV1jE411u7bx?from=search&seid=35153938940534319
梯度下降法
本算法由梯度下降所引申:
对于优化问题:

使用梯度下降:

注意,alpha也是可以算的:求一个a使得f(x0+aP0)最小,是求函数极值的,这时候是关于a的一个函数,所以对a求导求极小值,复合函数求导法则最后就会得到求导等于0,这时候的点是驻点,就是导数值为0的点,因为二阶导数黑塞矩阵正定,所以一定为极小值点。这时候就求出了在P0方向上的最小值点。
图中()意味内积。
共轭和预备知识
共轭:A共轭的定义

引申:非零向量如果共轭,则一定线性无关。

此图:只要a_i彼此正交,则xi很容易计算。
问题再次转化:要求x,可以用aplha表示,而alpha只和p有关
因此,只要给出一组A共轭的向量组,就可以把x写出来。
如何获得P?

怎么得到线性无关的向量组?
施密特正交法:【不断地做A-投影(指内积是A内积)】

共轭梯度下降算法

残量是梯度的相反数】
【图中的(AP0,R1)代表内积】
一二步和最速下降一样,对新的残量。
新的前进方向,让r1在P0上做投影,沿着共轭方向前进。
优点
- 可以证明,比梯度下降法收敛的快
- 可以证明能得到精确解
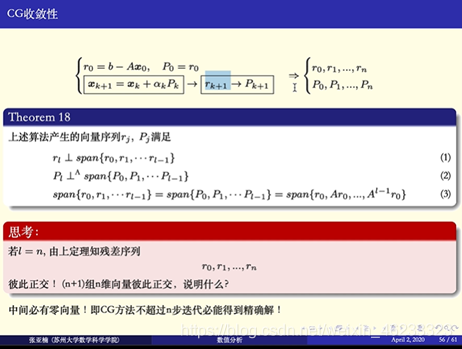
图中span代表子空间,可以证明是同一个子空间,最后一个等号是科里洛夫子空间
代码实现


此图中,去掉min res的注释即可得到梯度下降法代码。
例题


第二步迭代:【经评论区老哥提醒,下图P1的正负号写反了,感谢】
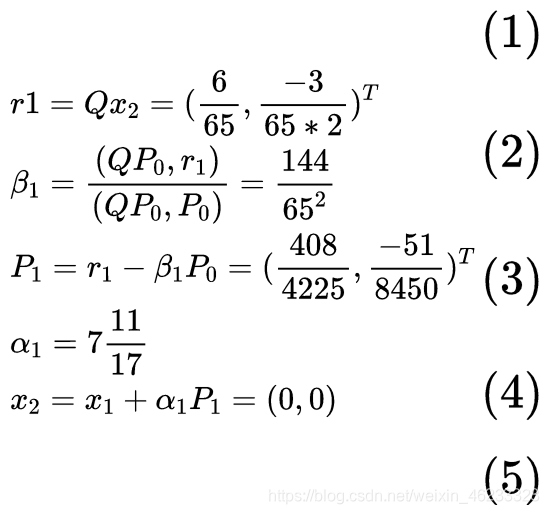
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








