背景
其实我一直瞧不上arima这种传统时间序列的模型,因为他们预测步长期数稍微长一点,例如预测个五期,十期,效果就会非常差,甚至是一条直线,完全没有办法忽悠老师或者是审稿人。
但是最近发现sarima带季节性的差分移动自回归模型的效果,对于像AQI空气质量这种具有季节性因素的数据效果还不错。并且这也是很多本科生常用的模型,并且我的数据案例里面还没有这种做时间序列arima的数据案例,所以本次就临时写一个案例。
既然是写案例,就不会只做一个模型,而是从最开始的画图,平稳性检验,自相关系数图,模型定阶,到后面的残差检验模,型预测,还有效果评估都会写在里面,是一个比较全面的流程案例。
注意那些什么拿传感器或者是锂电池寿命或者是什么轴承寿命的这种时间序列数据就不要用这个模型了。因为他们没有季节性,有的同学又要说了,那没有季节性我用arima不行吗?我又要无语了........自己去看看arima最早是运用于什么领域的(经济,农业,气象——都是很低频的数据,最多一天一个观测点),那些工业界的传感器都是几秒钟就收集一个数据点,并且它为什么不适用于这些工业上的数据?(平稳性检验大部分工业数据都通不过)。当然也不是绝对的,自己想试试也是可以试试的嘛。不过报错了就又别再来问我为什么了........建议多问问AI,我写的这些所有的数据分析案例都是很基础很简单的,AI全部都能看懂都会的。如果你觉得AI的表述不能让你满意,要么是你问题问的不好,要么你用的是国内比较lj的智障大模型........
数据介绍
AQI数据还真不太好找,找来的都是一些乱七八糟还没处理过的,我这里找了一个北京市的过去十几年的AQI数据集,非常详细,他每一年都是一个压缩包,然后压缩包里面有每一天是一个CSV文件表格。数据量还挺大,因为它每一天每一个小时就会发布在北京的很多地区的AQI监测的情况。

所以我们要进行一定的预处理,主要思路就是首先针对北京不同的地区,我们直接取平均值。然后针对每一天的aqi,我们直接取每一天的23点最后一小时刻的Aqi作为当天的aqi收盘值,相当于就变成了这一天的aqi的取值。
最终处理为这个样子的数据:

只需要2列,一列是时间以天为周期,一列是当天北京的AQI。
当然需要本次实验的全部数据以及代码文件的同学还是可以参考:北京AQI预测数据
处理的代码都在下面,我们从头开始实现代码吧。
代码实现
数据预处理
导入包:
import os
import zipfile
import pandas as pd定义以下处理函数:
# 定义处理单个文件夹的函数
def process_folder(folder_path):
# 存储每个日期的AQI均值
daily_aqi = []
# 遍历文件夹中所有CSV文件
for file_name in os.listdir(folder_path):
if file_name.endswith('.csv'):
file_path = os.path.join(folder_path, file_name)
try:
# 读取CSV文件
df = pd.read_csv(file_path)
# 检查是否有数据
if df.empty:
print(f"文件 {file_name} 是空的,跳过")
continue
# 筛选出'AQI'列数据
aqi_data = df[df['type'] == 'AQI']
# # 检查是否有AQI数据
# if aqi_data.empty:
# print(f"文件 {file_name} 中没有数据,跳过")
# continue
# 获取每天的最后一个小时
grouped = aqi_data.groupby('date')
for date, group in grouped:
last_hour = group.iloc[-1] # 获取最后一行
avg_aqi = last_hour.iloc[3:].mean() # 计算所有地点AQI的平均值
daily_aqi.append({'date': date, 'AQI': avg_aqi})
except pd.errors.EmptyDataError:
print(f"文件 {file_name} 为空或格式错误,跳过")
except Exception as e:
print(f"读取文件 {file_name} 时发生错误: {e}")
# 返回结果作为DataFrame
return pd.DataFrame(daily_aqi)
# 定义主函数,处理所有压缩包
def process_all_zip(zip_folder_path, output_file):
all_data = []
# 遍历所有压缩包
for zip_name in os.listdir(zip_folder_path):
if zip_name.endswith('.zip'):
zip_path = os.path.join(zip_folder_path, zip_name)
# 解压到临时文件夹
with zipfile.ZipFile(zip_path, 'r') as zip_ref:
temp_dir = os.path.join(zip_folder_path, 'temp')
zip_ref.extractall(temp_dir)
# 假设解压后是一个文件夹
folder_name = os.listdir(temp_dir)[0]
folder_path = os.path.join(temp_dir, folder_name)
# 处理文件夹中的CSV文件
data = process_folder(folder_path)
all_data.append(data)
# 删除临时文件夹
for root, dirs, files in os.walk(temp_dir, topdown=False):
for name in files:
os.remove(os.path.join(root, name))
for name in dirs:
os.rmdir(os.path.join(root, name))
os.rmdir(temp_dir)
print(f'{zip_name}处理完成')
# 合并所有数据
final_data = pd.concat(all_data, ignore_index=True)
# 保存到CSV文件
final_data.to_csv(output_file, index=False)
print(f"处理完成,结果已保存到 {output_file}")
# 调用主函数
zip_folder_path = './北京空气质量' # 替换为压缩包所在的文件夹路径
output_file = 'final_aqi_data.csv' # 输出文件名
process_all_zip(zip_folder_path, output_file)就这样一段代码一个函数,运行完之后,我们的所有的数据都从zip文件里面提取出来,并且也处理好了,合并到最后一个变成final_aqi_data.csv 这么一个csv文件里面去了。
如果看不懂的话就自己把这里面的代码拿出来,一行一行的问AI1行一行的运行吧。也不需要懂,反正只是处理数据的过程,甚至都可以不看,最后得到了这样一个final_aqi_data.csv 文件就行,我都放在上面的链接里了。下面就可以开始建模了。
数据分析 SARIMA建模
还是一样,先导入包:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.sans-serif']=['SimHei'] #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False读取数据,查看前五行
df=pd.read_csv('final_aqi_data.csv',parse_dates=['date']).set_index(['date']).sort_index()#
df.head()
描述性统计
df.info()
df.describe().T 可视化时间序列图:
可视化时间序列图:
df.plot(figsize=(14,4))
可以看到这十几年的波动真的是参差不齐,但整体来说还是一个较为正常的范围,偶尔某些天会比较高。
注意,上面的数据是以日度为频率的,但是我这里只是做一个演示的案例建模。我不想用这么多的数据。因为日度为频率,这十几年大概有3900多条数据,我觉得太多了,所以我想把它重采样为月度数据,将每一个月份的所有的日度数据求一个均值,就变成了这一个月的平均Aqi。
时间重采样
pandas的时间重采样超级简单:
data=df.resample('M').mean()
print(data.shape)
data.head()
可以看到数据变成了133个点,相当于11年的12个月,每个月一个数据,这样数据量就小很多。
然后再画图查看数据就会感觉很整洁:
df.resample('M').mean().plot(figsize=(14,4))
下面我们要划分训练集和测试集,因为我们要做一下模型的预测的效果的评估嘛,所以说我们得留出一年,也就是2024年这一年的AQI数据,12个点,去用来作为模型预测效果的评价的测试数据。
X=data
y=data['AQI']
#划分训练集和测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=12,shuffle=False)
print(X_train.shape,X_test.shape , y_train.shape,y_test.shape )
可以看到训练数据为121,测试数据为12。他们的时间范围打印如下
print(f'训练集的时间是从{X_train.index[0]}到{X_train.index[-1]},\n测试集的时间是从{X_test.index[0]}到{X_test.index[-1]} ')
定义评价指标
既然是回归问题那我们还是用常见的如下四个评价指标:

他们的代码都非常好实现,如下这样一个函数:
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error,r2_score
def evaluation(y_test, y_predict):
mae = mean_absolute_error(y_test, y_predict)
mse = mean_squared_error(y_test, y_predict)
rmse = np.sqrt(mean_squared_error(y_test, y_predict))
mape=(abs(y_predict -y_test)/ y_test).mean()
r_2=r2_score(y_test, y_predict)
return mae, rmse, mape,r_2 #mse准备工作完成后,下面正式开始进入建模过程。
SARIMA模型
首先还是导入包
from scipy import stats
import itertools
from statsmodels.tsa.seasonal import seasonal_decompose
import statsmodels.api as sm
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.tsa.statespace.sarimax import SARIMAX
from statsmodels.graphics.api import qqplot
from statsmodels.stats.diagnostic import acorr_ljungbox as lb_test
from statsmodels.tsa.stattools import adfuller我们把训练数据重新赋值给dta变量,并且重置索引查看:
dta=y_train.copy()
dta.index = dta.index.to_period('M')
dta.reset_index().info()
可以看到有两列,第一列是日期是,以月份为单位,第二列就是AQI,是浮点数。
序列图
画出时间序列图:
# 创建 Seaborn 折线图
plt.figure(figsize=(10, 4),dpi=128) # 设置图片大小
sns.lineplot(x='date', y='AQI', data=dta.to_timestamp().reset_index(), color='dodgerblue', linewidth=2.5,label='Train')
sns.lineplot(x='date', y='AQI', data=y_test.reset_index(), color='orange', linewidth=2.5,label='Test')
# 添加标题和轴标签
#plt.title("AQI", fontsize=16, fontweight='bold')
plt.xlabel("date", fontsize=14)
plt.ylabel("AQI", fontsize=14)
plt.legend()
# 显示图表
plt.tight_layout()
plt.show()
一目了然,谁是训练集,谁是测试集。并且我们可以从这个图,可以看到这个数据应该是具有一定的季节性的,而且有一定的下降的趋势性。
所以所以我们估计这个原始数据应该是不平稳的,因为它具有一定的下降的趋势。然后他也有季节性,所以说我们应该采用sarima模型,而不是arima模型。
平稳性检验
ADF单位根检验:
adfuller(dta)
这个要是看不懂就去问问AI哈,如果也不知道这些是指什么含义,建议多学学基础统计学。。。
简而言之,该单位根检验的p值是0.56,所以说在0.1的显著性水平下都没有办法拒绝原假设。所以说该数据是不平稳的。
所以下面我们就要对数据进行差分,差分之后再看是不是平稳的。
一阶差分后检验
代码也很简单差分就diff一下就可以了。我所有代码都是写的非常简洁的写法了。
adfuller(dta.diff().dropna())
可以看到p值是0.0001,说明一阶差分之后的数据在0.01的显著水平下是平稳的。
因此我可以确定我们的sarima模型里面的i,也就是差分阶数,为1。
季节性检验
对于季节性,最简单的观察就是分解之后画图出来看,我们用加法模型。
dta_s=dta.copy() ;
result = seasonal_decompose(dta_s.to_timestamp(), model='additive', period=12)
# 绘制分解结果
result.plot()
plt.gcf().set_size_inches(10, 8)
plt.gcf().set_dpi(128)
plt.show()
可以看到季节性很明显的,一年一个周期,所以我们的S参数是12, 因为我的数据是月度的,所以说十二个数据是一个周期如果是年度的话就应该是365。
然后也可以看到趋势项明显有一个下降的趋势,残差的话也较为均匀。
纯随机检验
也叫白噪声检验,检验这个数据是不是纯随机的,如果是纯随机就没有建模价值,如果不是纯随机就有建模的价值。
Ljung-Box 检验
lb_test(dta, return_df=True,lags=5)
五期的P值全部小于0.05,说明在0.05的显著性水平下,该数据不是纯随机序列。可以进行下一步建模。
模型定阶
由于我们的数据已经进行了差分, 所以说我们要对差分之后的数据画出ACF图和PACF图.
fig = plt.figure(figsize=(8, 5))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(dta.diff().dropna(), lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(dta.diff().dropna(), lags=40, ax=ax2)
plt.tight_layout()
plt.show()
一阶差分后序列的平稳性分析 从图像中可以观察到以下特点:
自相关函数(ACF)图: 在滞后 2时有显著峰值,其后迅速衰减,接近零附近波动。
偏自相关函数(PACF)图: 在滞后 2时存在一个显著的偏自相关峰值,其后各滞后阶的偏自相关系数接近零附近波动。
ARIMA 模型阶数的选择
自回归阶数 (AR 阶数) 偏自相关函数(PACF)在滞后 2 时存在显著峰值,之后快速衰减,这表明自回归部分可能是一个二阶模型。因此,初步判断 p=[0,2]范围。
移动平均阶数 q(MA 阶数) 自相关函数(ACF)在滞后 2 时也存在显著峰值,之后快速衰减,但13阶的时候又超出了置信区间,初步判断 p=[0,2]范围。
建议的模型 根据上述分析,建议组合对比。
由于是Sarima模型,我们还需要对季节性差分后的数据找到其阶数,首先画出季节差分后的序列图:
periodicity=12
seasonal_diff = dta.to_timestamp().diff(periods=periodicity).dropna()
# 绘制季节性差分后的数据
plt.figure(figsize=(9, 3))
plt.plot(seasonal_diff)
plt.title('Seasonally Differenced Time Series')
plt.show()
同样画出ACF和PACF图
fig = plt.figure(figsize=(8, 5))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(seasonal_diff, lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(seasonal_diff, lags=40, ax=ax2)
plt.tight_layout()
plt.show()
P和Q的范围为(0,2),虽然其在十二期左右右超出了置信区间范围,但是太长了,我们就不管了。也不知道哪一种最好。
所以我们遍历其阶数可能性,找到最好的。使用AIC信息准则来评价。
模型对比
p = range(0, 3) # 非季节部分 AR 的阶数
q = range(0, 3) # 非季节部分 MA 的阶数
P = range(0, 3) # 季节部分 AR 的阶数
Q = range(0, 3) # 季节部分 MA 的阶数
d = 1 # 非季节部分差分阶数
D = 1 # 季节部分差分阶数
s = 12 # 季节性周期长度(12期,月份或季度等)
# 遍历所有可能的参数组合
param_combinations = list(itertools.product(p, q, P, Q))
# 存储结果的列表
results = []
# 遍历参数组合,训练 SARIMA 模型并记录 AIC, SC 和调整𝑅2
for params in param_combinations:
try:
# 定义 SARIMA 模型
model = SARIMAX(dta,
order=(params[0], d, params[1]),
seasonal_order=(params[2], D, params[3], s),
enforce_stationarity=False,
enforce_invertibility=False)
# 拟合模型
result = model.fit(disp=False)
# 计算调整𝑅2
y_pred = result.fittedvalues
r2 = r2_score(dta, y_pred)
adjusted_r2 = 1 - (1 - r2) * (len(dta) - 1) / (len(dta) - len(result.params) - 1)
# 提取 AIC 和 SC
aic = result.aic
sc = result.bic
# 保存结果
results.append({
'模型': f"SARIMA({params[0]},{d},{params[1]})({params[2]},{D},{params[3]})[{s}]",
'调整𝑅2': round(adjusted_r2, 3),
'AIC': round(aic, 3),
'SC': round(sc, 3)
})
except Exception as e:
# 如果某个参数组合出错,则跳过
print(f"模型 SARIMA({params[0]},{d},{params[1]})({params[2]},{D},{params[3]})[{s}] 出现错误: {e}")
continue
# 转化为 DataFrame 并按 AIC 排序
results_df = pd.DataFrame(results)
results_df = results_df.sort_values(by='AIC').reset_index(drop=True)
results_df排个序看看:
results_df.sort_values(['AIC','调整𝑅2',],ascending=[True,False])
可以看到SARIMA(1,1,2)(2,1,2)[12]的AIC最小,我们就用这个模型好了。
拟合模型
arma_mod20 = SARIMAX(dta, order=(1, 1, 2), seasonal_order=(2, 1, 2, 12),enforce_stationarity=False,
enforce_invertibility=False)
results = arma_mod20.fit()
print(results.params)
查看模型具体情况
results.summary()
有的系数也是不很显著,不过无伤大雅。我懒得写分析了,让gpt写的分析:
~~~
这个SARIMAX模型尝试预测空气质量指数 (AQI)。让我们分析一下结果:
模型规格: 模型使用SARIMAX(1,1,2)x(2,1,2,12)规格。这意味着:
-
(1,1,2): 这是模型的非季节性部分。它包含一个自回归 (AR) 项 (p=1),一个差分 (I) 项 (d=1) 表明对数据进行了差分运算以使其平稳,以及两个移动平均 (MA) 项 (q=2)。
-
(2,1,2,12): 这是模型的季节性部分,周期为12(可能代表月度季节性)。它包含两个季节性AR项 (P=2),一个季节性差分 (D=1) 项,两个季节性MA项 (Q=2) 和季节性周期 (s=12)。
模型拟合:
-
对数似然: 较高的对数似然值表示更好的拟合。但是,如果没有与其他模型进行比较,则绝对值无法直接解释。
-
AIC、BIC、HQIC: 这些是用于比较模型的信息准则。较低的值表示更好的模型。AIC、BIC和HQIC之间的差异相对较小,表明模型的规格合理。
系数显著性:
一些系数具有统计学意义 (p值 < 0.05):
-
ar.L1: 一个显著的负自回归项。这表明当前AQI与前一时间段的AQI之间存在负相关关系。
-
ma.L2: 一个显著的负移动平均项。这表明当前误差与两个时间段前的误差之间存在负相关关系。
-
ar.S.L24: 一个显著的负季节性自回归项,滞后24(两年)。这表明当前AQI与两年前的AQI之间存在负相关关系。
其余系数(ma.L1、ar.S.L12、ma.S.L12、ma.S.L24)没有统计学意义(p值较高)。这表明它们可能没有对模型的预测能力做出有意义的贡献。可以考虑通过移除这些不显著的项来简化模型。
诊断测试:
-
Ljung-Box检验: Ljung-Box检验评估残差(误差)中是否存在自相关。高p值 (0.66) 表明残差中没有显著的自相关。这表明模型拟合良好。
-
Jarque-Bera检验: 此检验测试残差是否服从正态分布。高p值 (0.77) 表明残差近似服从正态分布。
-
异方差检验: 此检验测试残差的方差是否随时间保持不变。p值 (0.36) 表明此模型中异方差不是一个显著的问题。
总体而言:
SARIMAX模型在预测AQI方面显示出前景。但是,不显著系数的存在表明可以简化模型。仅使用显著系数(移除ma.L1、ar.S.L12、ma.S.L12、ma.S.L24)重新运行模型可能会提高模型的简约性和预测精度。诊断测试表明模型的假设在很大程度上得到了满足。进一步的分析可以包括检查残差图中的任何模式,并使用适当的指标评估模型的预测性能。此外,探索其他模型规范或结合其他相关预测变量可以提高模型的准确性。最后,ma.S.L12和ma.S.L24的极大标准误差值得进一步调查。
~~~
反正这个阶数有各有各的说法,如果觉得这个阶数不好的话,就换一个阶数试一试吧,反正也不可能做到完美。
残差检验
模型拟合完了,还需要检验残差,看残差是否是白噪声,即纯随机序列,如果残差不是白噪声,说明模型提取的规律不够充分,还需再处理。
首先要检验残差是否服从正态分布,画图查看,然后检验。
results.resid.plot(figsize=(10,3))
还行,虽然它不是很标准的正太,但是也是均匀的围绕在零轴附近上下波动。
# 使用 plot_diagnostics 方法生成残差诊断图
results.plot_diagnostics(figsize=(12, 8))
plt.tight_layout()
这个方法非常方便能够生成残差的所有的检验图,我们可以看到其直方图,序列图,QQ图和相关性系数图,所有的图都表示该数据其实有较好的正态性以及没有残差自相关。
残差LB检验
lb= lb_test(results.resid, return_df=True,lags=5)
print(lb)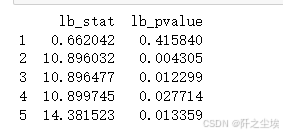
可以看到在0.05的显著性水平下,接受原假设,说明残差是纯随机序列,模型已经充分提取了数据里面的规律。拟合良好。
模型预测
forecast_steps = 12 # 想要预测的未来的月份数量
# last_date = dta.index[-1].to_timestamp() # 将最后一个月份转换为 Timestamp
# new_index = pd.date_range(start=last_date, periods=forecast_steps, freq='M')
forecast = results.forecast(steps=forecast_steps)
forecast.head()
arima_pred=forecast
df_eval=pd.DataFrame(columns=['mae','rmse','mape','R2'])
s=evaluation(y_test,arima_pred.to_numpy())
df_eval.loc['SARIMA测试集',:]=list(s)
#df_pred['ARIMA']=arima_pred.to_numpy()
df_eval
可以看到这是我们流出来的测试集上的预测值和真实值的误差。可能大家对这个误差的数值没什么感觉,我们画个图就知道它拟合效果好不好了。
预测对比图
我们先把这个模型在训练集上的预测值弄出来看一看。
predict_sunspots = results.predict("2014-01", "2024-01", )#dynamic=True)
print(predict_sunspots)
s=evaluation(y_train,predict_sunspots[:].to_numpy())
df_eval.loc['SARIMA训练集',:]=list(s)
df_eval
可以看到训练集上的误差反而还更大一点。可能是因为训练集的数据比较多吧。
最后一起画图。
plt.figure(figsize=(10,4),dpi=128)
plt.plot(dta.to_timestamp().index,dta,label='actual')
plt.plot(predict_sunspots.to_timestamp().index[1:],predict_sunspots[1:],label='predict')
plt.plot(y_test.to_period('M').to_timestamp().index,y_test.to_period('M').to_timestamp(),label='actual')
plt.plot(arima_pred.to_timestamp().index,arima_pred,label='predict')
plt.legend(['训练集真实值','训练集预测值','测试集真实值','测试集预测值'])
plt.xlabel('月份')
plt.ylabel('AQI')
plt.show()
这里是把训练集的真实值和预测值,还有测试集的预测值和真实值都画上去了,其实可以看到效果都还是不错的。
如果我们只想看测试级的情况我们就单独在画个图:
plt.figure(figsize=(8,3),dpi=128)
plt.plot(y_test.to_period('M').to_timestamp().index,y_test.to_period('M').to_timestamp(),color='g')
plt.plot(arima_pred.to_timestamp().index,arima_pred, color='r')
plt.legend(['测试集真实值','测试集预测值'])
plt.xlabel('月份')
plt.ylabel('AQI')
plt.show()
效果还不错。
整体这样一套时间序列sarima的全流程就差不多结束了。
我们做了数据的预处理,重采样,时间序列画图,平稳性检验,季节性检验,纯随机性检验,差分模型阶数确定。残差检验,模型预测,模型评估以及可视化。我觉得已经非常全面了,很多同学用r语言都不一定能有我这Python做的全面。
并且用Python跟其他的一些什么模态分解或者是神经网络去做结合创新还是很方便的。这样的一个工作量差不多可以做一个本科生的毕业论文吧。
创作不易,看官觉得写得还不错的话点个关注和赞吧,本人会持续更新python数据分析领域的代码文章~(需要定制类似的代码可私信)

























 1047
1047

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










