前言
深度监督网络(DSN)可以提高隐藏层学习过程的直接性和透明度。本文注意力集中在卷积神经网络(CNN型)架构的三个方面:
- (1)影响中间层的透明度具有整体分类;
- (2)学习特征的辨别力和稳健性,特别是在早期阶段;
- (3)面对消失的“梯度”训练有效性。
为了解决这些问题,我们在每个隐藏层引入伴随目标函数,以及输出层的整体目标函数(与分层预训练不同的集成策略)。我们还使用随机梯度方法扩展的技术分析我们的算法。
DSN的核心思想是为隐藏层提供集成的直接监督层,而不是仅在输出层提供监督,并将此监督传播回早期层的标准方法。我们通过为每个隐藏层引入伴随目标函数来提供这种集成的直接隐藏层监督;这些伴随目标函数可以被视为学习过程中的附加(软)约束。
使用来自随机梯度方法的分析技术来研究限制性设置,其中并入伴随目标函数直接导致提高的收敛率。这种综合深度监督的优势是显而易见的:
- (1)对于小型训练数据和相对较浅的网络,对于分类准确性和学习特征问题,深度监督可以提供强大的“正规化”;
- (2)用于大型训练数据和更深层次的网络深度监控使得利用极深度网络可以通过改善其他有问题的收敛行为来使的性能增益提升。
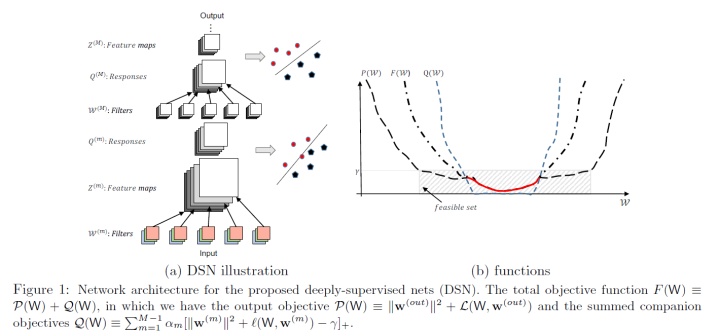
DSN的主要特征是通过伴随目标对深度监督进行综合编制,在最简单的情况下,其形式几乎与输出层的目标函数相同,如下公式所示:
- 但是在初始化和重新调整的时候过度的使用这种分层预训练容易导致过拟合。
- 我们注意到我们DSN的方法独立于averaging [22],drop-connect [17]和Maxout [10]等技术; 因此,我们如果将DSN与这些技术相结合可能会使分类误差大大减少。
Deeply-Supervised Nets
- DSD是在现有的CNN基础上提出来的,在隐藏层引入了分类器(SVM或Softmax)。
DSN提出的动机
- 一般来说,在较多的特征上训练判别分类器比在较少的特征上训练判别分类器的性能要更好,如果讨论的特征是深层网络中的隐藏层特征,意味着使用这些隐藏层特征图训练的判别分类器的性能可以作为这些隐藏层特征图的质量好坏的评判标准(我猜论文应该是表达这个意思)。
- 我们还期望这种深度监督可以缓解消除“渐变”的常见问题。我们通过将“伴随”分类输出与每个隐藏层相关联来引入我们的额外深度反馈。实证结果表明了伴随目标的以下主要特性:
- (1)它是一个特征正则化的类型,它导致测试误差的减少,而不一定减少训练误差;
- (2)它导致改进的对流性能行为,需要更少的手动调整(特别是对于非常深的网络)。
公式
- 将一个分类与每个隐藏层相关联。 对应的权重表示为:
- 为了便于参考,我们将总体提目标函数定义为:
- 其中P(W)为输出层的目标函数,定义如下:
- 隐藏层伴随目标函数如下:
- 在上述公式中,w(out)表示输出层权重,那么我们的总体目标函数F(W)就可以表示为:
- 我们使用SGD训练DSN模型,梯度W遵循传统的CNN模型,加上来自隐藏层直接监督的梯度;我们还使用伴随目标归零,如下所述,我们将
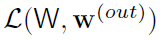 (与输出层相关)称为总损失,将
(与输出层相关)称为总损失,将 称为伴随损失。在L2SVM中这些都是预测误差的损失。
称为伴随损失。在L2SVM中这些都是预测误差的损失。 - 出来学习卷积核和权重W之外,我们在每个隐藏层包含了一个额外的目标,与该层的良好标签预测相关联,这个额外的目标强烈支持在每个隐藏层上具有辨别力和敏感性的特征。
- 注意:对于每一个
 ,w(m)取决于Z(m)(
,w(m)取决于Z(m)(Z(m)表示中间层的输出),而Z(m)又取决于第一到m层。 - 在训练过程中经常被送到零;这意味着产生良好的输出层分类的总体目标不会从根本上改变,而且这个目标可以作为一种正则化或作为判别特征的代理。在公式(4)中我们追求这种伴随目标归零的一种方法是设置一个阈值γ(超参数)。一旦每个隐藏层的伴随损失低于阈值,它就会消失(我理解的是伴随目标函数不再工作),不再有助于学习过程中的梯度更新(见上述的公式4便可知)。第m个平衡参数αm表示输出目标与相应的伴随目标之间的权衡。
- 伴随目标归零的另一种方法是使用简单的衰减函数,例如
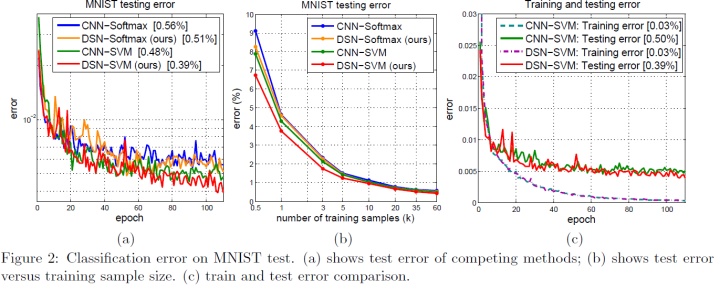
αm × 0.1 × (1 − t/N) → αm强制F(W)的第二个项在一定次数的迭代后消失,其中t是当前迭代步数,N是总迭代步数。我们从这两种方法中获得了可观的初步结果; - 最先进的基准测试结果表明,深度监督方法不会显示有害的过拟合:如图(2.c)所示,而CNN和DSN的训练误差最终接近于零,DSN 显示出较低的测试误差,因此证明了其优于标准CNN的优势。
随机梯度下降视图(Stochastic Gradient Descent View)
- 深度神经网络中的目标函数是高度非凸函数,这一特征导致当前缺乏对DL框架的清晰数学/统计分析。 一种常见的方法是通过将注意力仅限于局部凸性所处的环境来提高可追溯性。 在这里,我们遵循这个例子,假设我们的目标函数是λ-strongly局部凸的,并遵循随机梯度下降的分析技术[3]。
- λ-strongly 凸函数F(W)定义如下(对W if ∀ W,W′ ∈ W and any subgradient g at W):
- 令W⋆为最优解,假设凸函数设置中存在E[∥WT −W⋆∥2]和E[F(WT ) − F(W⋆)]的上界。或者说在凸函数设置中存在E[F(WT ) − F(W⋆)]的上界。在这个基础上我们试着去理解目标函数的收敛性,图一(b)大致可以说明E[∥WT −W⋆∥2]假设特征。 在[19]中,给出了具有局部凸函数的M-估计量的收敛速度,其具有成分损失和规则化项。
- 定义:用
Sγ(F) = {W | F(W) ≤ γ}表示γ-sublevel集合,在这里等价于F(W) ≡ P(W) + Q(W). - 接下来论文中是证明
Sγ(F) = {W | F(W) ≤ γ}于F(W) ≡ P(W) + Q(W)等价的过程,我把这部分过程省略了。
实验
- 文章中在四个数据集上评估我们提出的DSN:MNIST,CIFAR-10,CIFAR-100和SVHN。还使用ImageNet来评估DSN在大型数据集上的行为。
- 使用小批量大小为128且固定动量为0.9的SGD求解器。学习率和体重衰减因子的初始值由评估集确定。
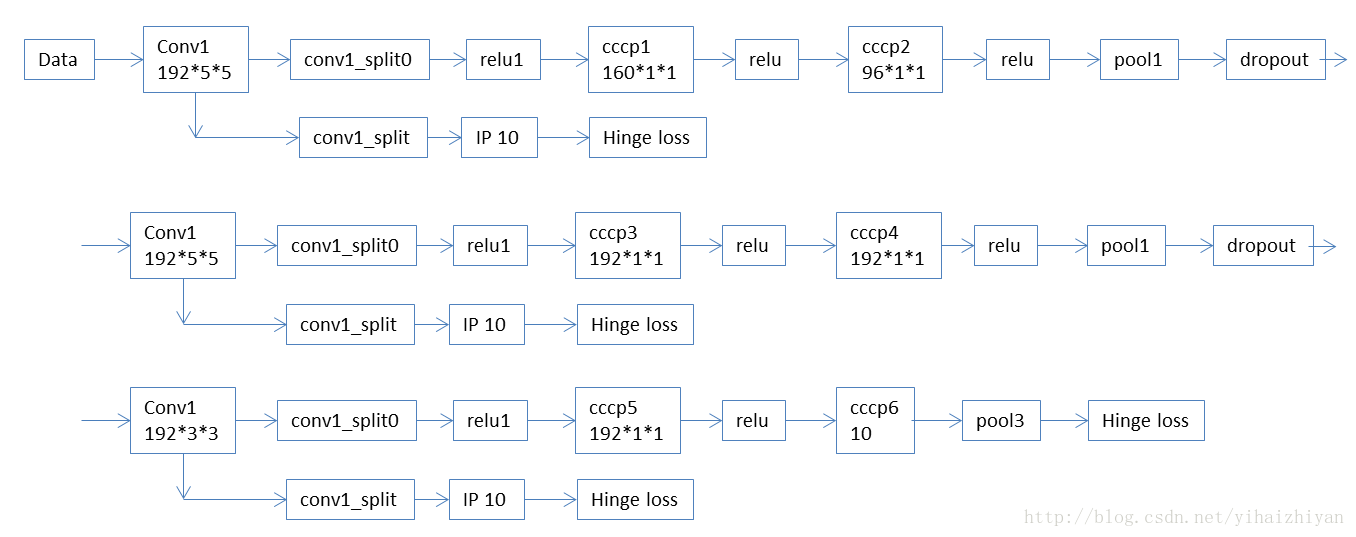
- 我们还包含两个丢失率为0.5的丢失层。 卷积层上的伴随目标被强制反向传播去指导误分类的相关层。我们提出的DSN框架并不难以训练,也没有采用特定的工程技巧。
- DSN可以配备不同类型的分类目标功能;我们考虑L2SVM和softmax,并显示DSN-L2SVM和DSN-Softmax性能超过相应的CNN-L2SVM和CNN-Softmax方法,如图2.a所示,在小型训练数据体系中,性能提升更为明显(见图(2.b));这可能部分减轻了DL需要大量训练数据的负担。
总的来说,我们在所有四个数据集上都观察到了最新的分类错误。所有结果都是在没有
aver- aging(我的理解是没有均值化)的情况下实现的[22],这可以进一步提高分类精度。我们的DSN方法可以与许多现有的CNN类型方法结合使用。总体而言,如前所述:对于小型训练数据和相对较浅的网络,DSN起到强大的“正规化”的作用;对于大型训练数据和非常深的网络,DSN使训练过程变得方便,
总结
这篇论文首次提出
deeply -supervision的做法,文章的motivation基于这样的观察: 如果features越discrminative, 那么classifier的性能就越好 。文章还提到
deeply- supervision的优点包括:能够减轻梯度爆炸或梯度消失,收敛速度更快(辅助 loss 将误差直接注入中间层,有点类似于
resnet的机制,不同的是 loss 来源不同 )辅助 loss 起到
regularization的作用 (我猜应该是超参 λ起得作用)作者可视化了第一卷积层学到的
feature map, 发现比普通 CNN 学到的特征更加intuitive(论文提到了这一现象,但没有给出解释,后面几层特征图的特点也没有提及).
文章里的辅助分类器为 SVM。
后记
- 论文后面的内容都是对数据集合实验精度的介绍,我没有详细写了。
- paper下载:http://arxiv.org/abs/1409.5185
- code 和prototxt文件下载:https://github.com/s9xie/DSN







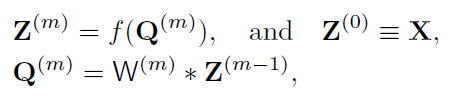
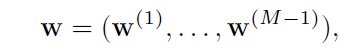
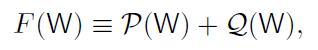
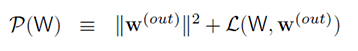
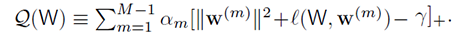
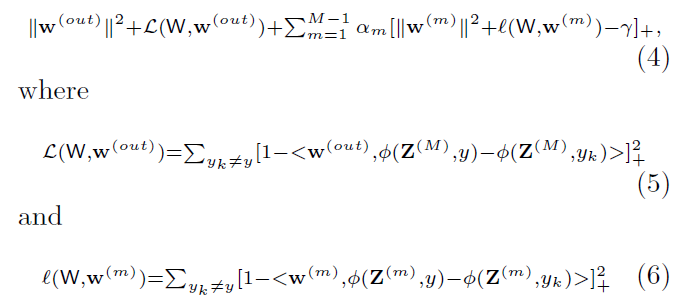
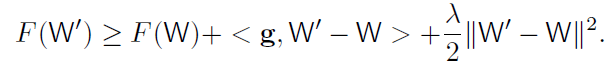

















 820
820

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










