最小二乘法

最小二乘法说白了就是最小平方法，最小二乘法到底是怎么一回事呢？
网上找了很多资料，对最小二乘法也有了一些认识
最小二乘法是一种数学优化技术，其通过最小化误差的平方和寻找数据的最佳函数匹配；利用最小二乘法可以简便的求得未知的数据，并使得这些求得得数据与实际数据之间误差的平方和最小。
简而言之，最小二乘法和梯度下降法类似，都是一种求解无约束最优化问题的常用方法，并也可以用于曲线拟合，来解决回归问题。

一、简单理解二乘法

比如采样获取到一批样本，$(x_1,y_1)$,$(x_2,y_2)$…$(x_n,y_n)$,得到这批数据之后，接下来要处理这堆数据，假设$y$跟$x$呈线性关系，即$y={\beta }_0+{\beta }_{1}x$,接下来所需要做的就是根据采样获得的数据来求解${\beta }_0$和${\beta }_1$了。

二、最小二乘法的误差

假设有五个尺子测量同一个线段，会得到五个不同的值10.2，10.3，9.8，9.9，9.8，之所以出现不同值的原因可能是尺子材质不一样；厂家生产的精度不一样等等…总之就是会产生误差，而一般在这种情况，会取平均值作为最终线段的长度，即$\overline{x}=\frac{10.2+10.3+9.8+9.9+9.8}{5}=10$,但是为什么一定要用$\overline{x}$呢，用中位数不行吗，用调和平均数不行吗？下面我们来思考一下这个问题。

如图，将这五个点画入坐标系中，记作$y_i$，其次把要猜测的真实值用平行于横轴的直线表示（虚线表示），这个$y$是用$y={\beta }_0+{\beta }_{1}x$算出来的猜测值，记作$y$，每个点都向$y$做垂线，每一段垂线的长度是$|y_i-y|$,也就是真实值和测量值之间的误差，因为误差是长度，且计算起来很麻烦，所以干脆就会用平方和来代表误差：
$|y_i-y|\to (y_i-y{)}^2$
由此，误差用数学公式表示就是：$$Q=\sum _{i=1}^n(y-y_i{)}^2$$
由于$y$是猜测的，故可以不断变换，同时$Q$也会不断变化

知道误差的表示之后，让总的误差最小的$y$就是真值，这是基于，如果误差是随机的，应该围绕真值上下波动。
即$Q=min{\sum }_{i=1}^n(y-y_i{)}^2$求这个就好求了;
一般套路：求导$\to$导数为0$\to$求出来的$y$就是真值
$$\frac{dQ}{dy}=\frac{d}{dy}\sum _{i=1}^n(y_i-y{)}^2=2\sum _{i=1}^n(y_i-y)$$
$$=2[(y_1-y)+(y_2-y)+(y_3-y)+(y_4-y+(y_5-y)]=0$$
$$y=\frac{y_1+y_2+...y_5}{5}$$求出来的y正好是平均数，原来算数平均数可以让误差最小啊，那看来选它也不无道理。
需要注意的是，误差的分布是一个正态分布，为什么呢？
假设直线对于坐标 $x_i$ 给出的预测 $f(x_i)$ 是最靠谱的预测，所有纵坐标偏离 $f(x_i)$ 的那些数据点都含有噪音，是噪音使得它们偏离了完美的一条直线，一个合理的假设就是偏离路线越远的概率越小，具体小多少，可以用一个正态分布曲线来模拟，这个分布曲线以直线对 $x_i$ 给出的预测$f(x_i)$ 为中心，实际纵坐标为 $y_i$ 的点$(x_i,y_i)$发生的概率就正比于 $e^{[-(\Delta y_i{)}^2]}$，这也就是误差分布服从正态分布的原因所在了。
在解决第一个问题之后，我们来思考下一个问题，根据采样得到的数据，该怎么求得参数${\beta }_0$和${\beta }_1$呢

三、最小二乘法的求解

知道了前面的cost function之后，下面的求解过程就很简单了
样本的回归方程为：$$Q=\sum _{i=1}^n(y_i-{\beta }_0-{\beta }_1{x}_i)$$
现在需要确定${\beta }_0$和${\beta }_1$来使得cost function最小，即$minQ$,所以依旧是那几步求解过程：求导$\to$(偏)导数为0$\to$求出${\beta }_0$,${\beta }_1$
具体过程如下：
$$\frac{\partial Q}{\partial {\beta }_0}=2\sum _{i=1}^n(y_i-{\beta }_0-{\beta }_1{x}_i)(-1)=0$$
$$\frac{\partial Q}{\partial {\beta }_1}=2\sum _{i=1}^n(y_i-{\beta }_0-{\beta }_1{x}_i)(-x_i)=0$$
将这两个方程整理一下，应用克莱姆法则即可求解出来，鉴于初学者可能有的不知道克莱姆法则，可以看一下克莱姆法则(用这个求解要求$D\ne 0$)

$$D=\left|\begin{array}{cc}n& {\sum }_{i=1}^n{x}_i\\ {\sum }_{i=1}^n{x}_i& {\sum }_{i=1}^n{x}_i^2\end{array}\right|=n\sum _{i=1}^n{x}_i^2-(\sum _{i=1}^n{x}_i{)}^2$$
$$D_1=\left|\begin{array}{cc}{\sum }_{i=1}^n{y}_i& {\sum }_{i=1}^n{x}_i\\ {\sum }_{i=1}^n{x}_i{y}_i& {\sum }_{i=1}^n{x}_i^2\end{array}\right|=\sum _{i=1}^n{x}_i^2{y}_i-\sum _{i=1}^n{x}_i\sum _{i=1}^n{x}_i{y}_i$$
$$D_2=\left|\begin{array}{cc}n& {\sum }_{i=1}^n{y}_i\\ {\sum }_{i=1}^n{x}_i& {\sum }_{i=1}^n{x}_i{y}_i\end{array}\right|=n\sum _{i=1}^n{x}_i{y}_i-\sum _{i=1}^n{x}_i{y}_i$$
$${\beta }_0=\frac{D1}{D}=\frac{{\sum }_{i=1}^n{x}_i^2{y}_i-{\sum }_{i=1}^n{x}_i{\sum }_{i=1}^n{x}_i{y}_i}{n{\sum }_{i=1}^n{x}_i^2-({\sum }_{i=1}^n{x}_i{)}^2}$$
$${\beta }_1=\frac{D2}{D}=\frac{n{\sum }_{i=1}^n{x}_i^2-({\sum }_{i=1}^n{x}_i{)}^2}{n{\sum }_{i=1}^n{x}_i^2-({\sum }_{i=1}^n{x}_i{)}^2}$$
根据这个公式，就可求解出对应的参数。

四、推广到矩阵形式

假设一个样本有更多的特征，也就是一个样本会有多个模型变量，（注：这里面表示样本用$x_1,x_2...x_n$，表示多个特征(模型变量)用$x^1,x^2...x^n$
在一个样本里，可以用如下线性函数表示：$$y={\beta }_0+{\beta }_1{x}^1+{\beta }_2{x}^2+...+{\beta }_m{x}^m$$
而对于n个样本来说，可以用如下线性方程组表示：
${\beta }_0+{\beta }_1{x}_1^1+{\beta }_2{x}_1^2+...+{\beta }_m{x}_1^m=y_1$
${\beta }_0+{\beta }_1{x}_2^1+{\beta }_2{x}_2^2+...+{\beta }_m{x}_2^m=y_2$
${\beta }_0+{\beta }_1{x}_3^1+{\beta }_2{x}_3^2+...+{\beta }_m{x}_3^m=y_3$
…
${\beta }_0+{\beta }_1{x}_n^1+{\beta }_2{x}_n^2+...+{\beta }_m{x}_n^m=y_n$
上述线性方程组可以表示为为：
$$\left[\begin{array}{ccccc}1& x_1^{(1)}& x_1^{(2)}& \cdots & x_1^{(m)}\\ 1& x_2^{(1)}& x_2^{(2)}& \cdots & x_2^{(m)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& x_n^{(1)}& x_n^{(2)}& \cdots & x_n^{(m)}\end{array}\right].\left[\begin{array}{cc}{\beta }_0& \\ {\beta }_1& \\ \cdots & \\ {\beta }_m& \end{array}\right]=\left[\begin{array}{cc}{y}_0& \\ y_1& \\ \cdots & \\ y_n& \end{array}\right]$$
将样本矩阵$x_i^j$记为矩阵A，将参数记为向量$\beta$，将真实值记为向量$Y$
即$A\beta =Y$
对于最小二乘法来说，最终矩阵表达形式可记为$$min||A\beta -Y|{|}_2$$
最后的最优解即为：$$\beta =(A^{T}A{)}^{-1}{A}^{T}Y$$
方程解法如下：

其中倒数第二行中的中间两项为标量，所以二者相等。然后利用该式对向量$\beta$求导：
由矩阵的求导法则：

可知该式的结果为：

令上式结果=0可得：

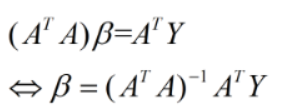
即为最小二乘法的解析解，它是一个全局最优解。

五、最小二乘法的改进

经典的最小二乘法使用起来足够简单粗暴，其考虑了每个样本的贡献，即每个样本具有相同的权重，但是有一个问题就是对噪声的容忍度很低（很敏感），即使得他对异常点比较敏感，因此提出了加权最小二乘法，相当于给每个样本设置了一个权重，以此来反映样本的重要程度或者是对解的影响程度。