
第一种方法:画图
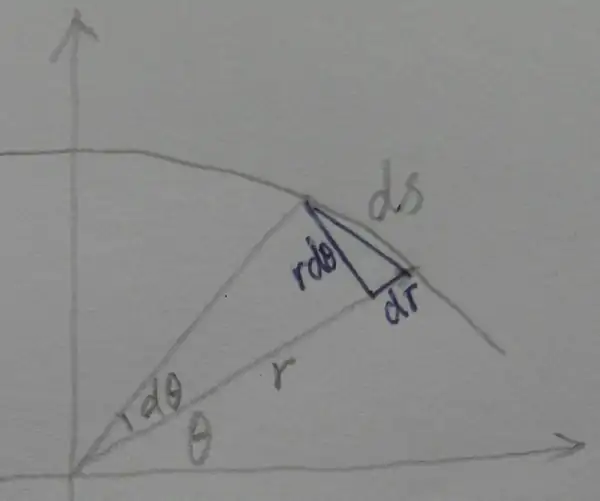
极坐标下的曲线r(θ)如上图。
所求ds用图中三角形斜边代替,
三角形近似为直角三角形。
有:
ds=√((rdθ)²+(dr)²)
=√((rdθ)²+(dr/dθ)²(dθ)²)
=√(r²+(dr/dθ)²) dθ
=√(r²+r'²) dθ
第二种方法:纯计算求导



极坐标下的曲线r(θ)如上图。
所求ds用图中三角形斜边代替,
三角形近似为直角三角形。
有:
ds=√((rdθ)²+(dr)²)
=√((rdθ)²+(dr/dθ)²(dθ)²)
=√(r²+(dr/dθ)²) dθ
=√(r²+r'²) dθ

 1328
1328
 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


