最短路径是指在有向或无向图中从一个起始节点到一个目标节点的最短路径。最短路径算法是指解决这个问题的一类算法。
最短路径算法包括贪心算法、Dijkstra算法、Bellman-Ford算法和Floyd-Warshall算法等。这些算法的原理和实现方法有所不同,但都是基于不同的思路来求解图中的最短路径。
贪心算法是一种启发式算法,它每次选择当前状态下最优的解,不考虑之后的结果。它可以用于求解单源最短路径,但是不适用于存在负边权的情况。
Dijkstra算法是一种广度优先搜索算法,它从起点开始,依次确定到每个节点的最短路径。该算法适用于无负边权的情况,并且可以处理负边权的情况,但前提是没有负权回路。
Bellman-Ford算法是一种动态规划算法,可以处理负边权的情况,但前提是没有负权回路。它的思路是从源节点开始,对所有边进行N-1轮松弛操作,其中N是节点的个数。
Floyd-Warshall算法是一种动态规划算法,它可以处理任意两点之间的最短路径,同时可以处理负权边,但也不能处理负权回路。
总之,最短路径算法是解决图中最短路径问题的重要算法,根据实际应用场景选择合适的算法可以提高算法效率和准确性。

一、C 最短路径 源码实现及详解
C语言中实现最短路径算法通常使用图论中的Dijkstra算法或者Floyd算法,下面分别进行介绍。
- Dijkstra算法
Dijkstra算法是一种贪心算法,用于求解带权有向图或无向图中的单源最短路径问题。其基本思想是:将所有顶点分成两个集合,一个集合(S)中包含已经求得最短路径的顶点,另一个集合(V-S)中包含尚未求得最短路径的顶点。每次从集合V-S中选取当前距离源点最近的顶点u,将其加入集合S,并更新从源点到集合V-S中各个顶点v的距离。重复执行此过程,直到集合V-S为空或者找不到更短的路径。
Dijkstra算法的时间复杂度为O(n^2),其中n为图的顶点数。下面给出使用邻接矩阵实现Dijkstra算法的C语言代码:
#include <stdio.h>
#include <stdlib.h>
#define INF 65535 //定义无穷大
void Dijkstra(int **graph, int n, int start, int *dist, int *prev)
{
int *visited = (int *)malloc(n * sizeof(int)); //记录顶点是否已经访问过
for (int i = 0; i < n; i++)
{
dist[i] = graph[start][i]; //初始化距离数组和前驱数组
prev[i] = start;
visited[i] = 0;
}
visited[start] = 1; //标记源点已经访问过
dist[start] = 0; //源点到自身的距离为0
for (int i = 0; i < n; i++)
{
int min_distance = INF;
int u;
for (int j = 0; j < n; j++) //找到距离源点最近的未访问顶点
{
if (!visited[j] && dist[j] < min_distance)
{
min_distance = dist[j];
u = j;
}
}
visited[u] = 1; //将该顶点标记为已访问
for (int k = 0; k < n; k++) //更新源点到未访问顶点的距离
{
if (!visited[k] && graph[u][k] != INF && (min_distance + graph[u][k] < dist[k]))
{
dist[k] = min_distance + graph[u][k];
prev[k] = u;
}
}
}
free(visited);
}
int main()
{
int n = 6; //图的顶点数
int **graph; //邻接矩阵
graph = (int **)malloc(n * sizeof(int *));
for (int i = 0; i < n; i++)
{
graph[i] = (int *)malloc(n * sizeof(int));
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
graph[i][j] = INF; //初始化邻接矩阵
}
}
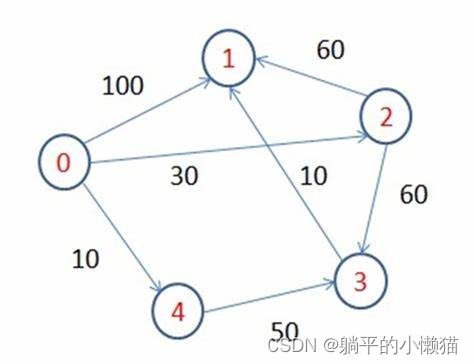
graph[0][1] = 1;
graph[0][2] = 12;
graph[1][2] = 9;
graph[1][3] = 3;
graph[2][4] = 5;
graph[3][2] = 4;
graph[3][4] = 13;
graph[3][5] = 15;
graph[4][5] = 4;
int *dist = (int *)malloc(n * sizeof(int)); //距离数组
int *prev = (int *)malloc(n * sizeof(int)); //前驱数组
Dijkstra(graph, n, 0, dist, prev);
printf("最短路径为:\n");
for (int i = 1; i < n; i++)
{
printf("%d ", i);
int j = i;
while (prev[j] != 0)
{
printf("<--%d", prev[j]);
j = prev[j];
}
printf("<--%d", 0);
printf("\n");
}
printf("最短距离为:\n");
for (int i = 0; i < n; i++)
{
printf("%d ", dist[i]);
}
printf("\n");
free(dist);
free(prev);
for (int i = 0; i < n; i++)
{
free(graph[i]);
}
free(graph);
return 0;
}
- Floyd算法
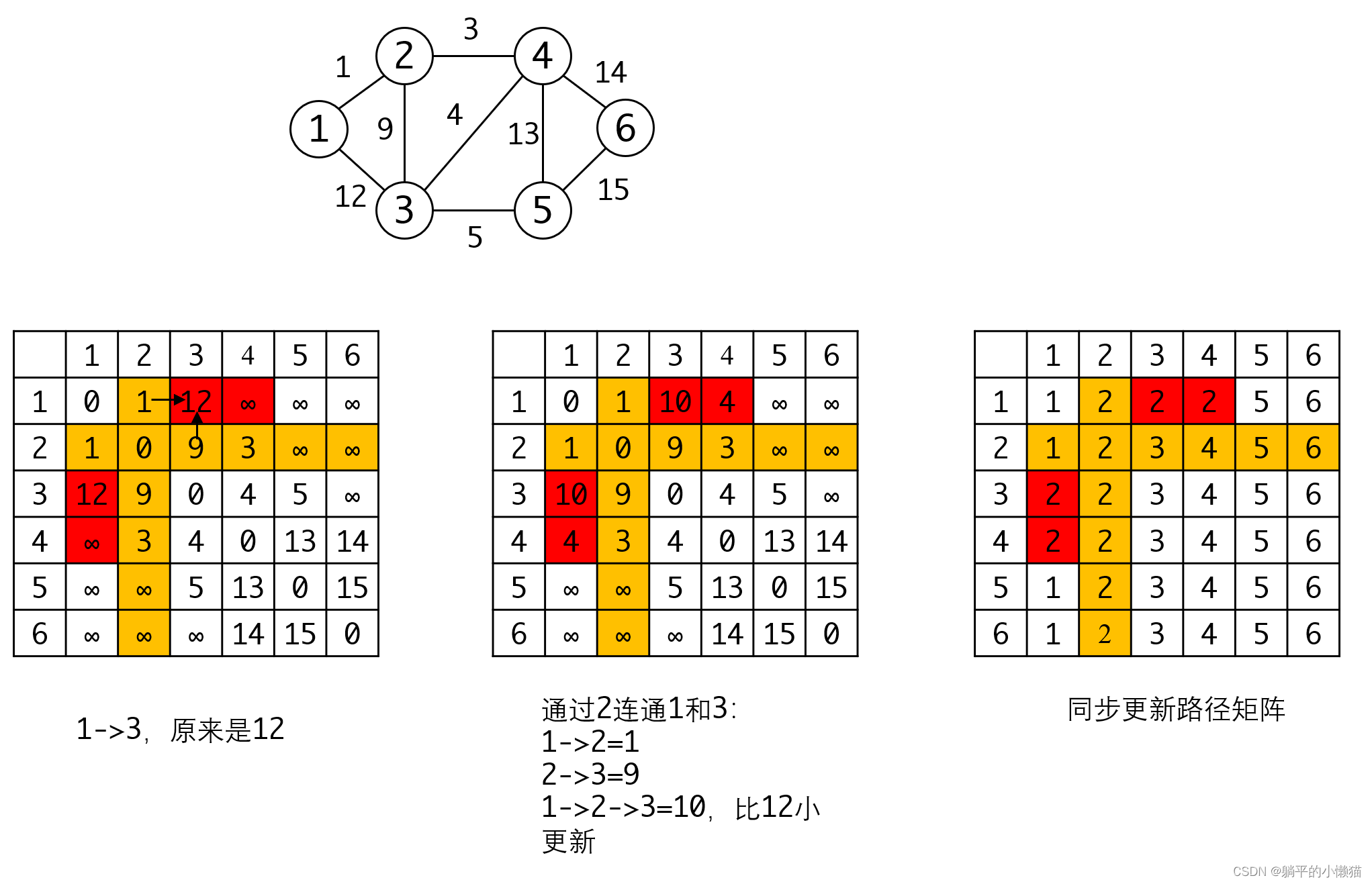
Floyd算法是一种动态规划算法,用于求解带权有向图中多源最短路径问题。其基本思想是:先对图进行预处理,求出任意两个顶点之间的最短路径长度,然后根据最短路径长度构造出最短路径。算法的核心是一个三重循环,其中第一重循环枚举中间节点,第二重循环枚举起点,第三重循环枚举终点,用起点到中间节点的距离加上中间节点到终点的距离与起点到终点的距离作比较,更新最短距离。
Floyd算法的时间复杂度为O(n^3),其中n为图的顶点数。下面给出使用邻接矩阵实现Floyd算法的C语言代码:
#include <stdio.h>
#include <stdlib.h>
#define INF 65535 //定义无穷大
void Floyd(int **graph, int n, int **dist, int **prev)
{
for (int i = 0; i < n; i++) //初始化距离数组和前驱数组
{
for (int j = 0; j < n; j++)
{
dist[i][j] = graph[i][j];
if (i != j && graph[i][j] < INF)
{
prev[i][j] = i;
}
else
{
prev[i][j] = -1;
}
}
}
for (int k = 0; k < n; k++)
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (dist[i][j] > dist[i][k] + dist[k][j])
{
dist[i][j] = dist[i][k] + dist[k][j];
prev[i][j] = prev[k][j];
}
}
}
}
}
int main()
{
int n = 6; //图的顶点数
int **graph; //邻接矩阵
graph = (int **)malloc(n * sizeof(int *));
for (int i = 0; i < n; i++)
{
graph[i] = (int *)malloc(n * sizeof(int));
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
graph[i][j] = INF; //初始化邻接矩阵
}
}
graph[0][1] = 1;
graph[0][2] = 12;
graph[1][2] = 9;
graph[1][3] = 3;
graph[2][4] = 5;
graph[3][2] = 4;
graph[3][4] = 13;
graph[3][5] = 15;
graph[4][5] = 4;
int **dist = (int **)malloc(n * sizeof(int *)); //距离数组
int **prev = (int **)malloc(n * sizeof(int *)); //前驱数组
for (int i = 0; i < n; i++)
{
dist[i] = (int *)malloc(n * sizeof(int));
prev[i] = (int *)malloc(n * sizeof(int));
}
Floyd(graph, n, dist, prev);
printf("最短路径为:\n");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
二、C++ 最短路径 源码实现及详解
下面是一个使用 Dijkstra 算法实现最短路径的 C++ 代码:
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;
// 定义一个无穷大的常量
const int INF = INT_MAX;
// 存储图的邻接表类型
typedef pair<int, int> Edge; // 权重,目标节点
typedef vector<vector<Edge>> Graph;
// Dijkstra 算法函数,返回从起点到各个节点的最短路径
vector<int> dijkstra(const Graph& graph, int start) {
// 初始化距离向量和最短路径向量
int n = graph.size();
vector<int> distances(n, INF);
vector<int> parents(n, -1);
distances[start] = 0;
// 创建一个小根堆,存储节点编号和距离
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> minHeap;
minHeap.push({0, start}); // 距离为 0,起点编号为 start
while (!minHeap.empty()) {
int currNode = minHeap.top().second;
int currDist = minHeap.top().first;
minHeap.pop();
// 如果当前距离比已知的最短路径更长,则忽略这个节点
if (currDist > distances[currNode]) {
continue;
}
// 遍历当前节点的邻居节点
for (auto neighbor : graph[currNode]) {
int nextNode = neighbor.second;
int dist = currDist + neighbor.first;
// 如果到达邻居节点的路径更短,则更新邻居节点的距离和父节点
if (dist < distances[nextNode]) {
distances[nextNode] = dist;
parents[nextNode] = currNode;
minHeap.push({dist, nextNode});
}
}
}
return distances;
}
// 调用 dijkstra 算法函数并打印结果
int main() {
int n, m, start;
cin >> n >> m >> start;
// 创建一个邻接表表示的图
Graph graph(n);
for (int i = 0; i < m; i++) {
int from, to, weight;
cin >> from >> to >> weight;
graph[from].push_back({weight, to});
}
// 调用 dijkstra 算法函数求最短路径
vector<int> distances = dijkstra(graph, start);
// 打印结果
for (int i = 0; i < n; i++) {
if (distances[i] == INF) {
cout << "INF" << endl;
} else {
cout << distances[i] << endl;
}
}
return 0;
}
在这个实现中,我们首先定义了一个 Edge 结构体来表示图中的一条边,包含一个权重和一个目标节点编号。然后,我们使用 vector<vector<Edge>> 来表示图的邻接表,其中 graph[i] 存储了节点 i 的邻居节点和边权重。接着,我们实现了一个名为 dijkstra 的函数,使用 Dijkstra 算法求出从起点到各个节点的最短路径,并返回一个距离向量。最后,我们在 main 函数中读入图的信息,调用 dijkstra 函数,然后输出距离向量。
在 Dijkstra 算法中,我们首先初始化距离向量和最短路径向量,将起点的距离设为 0,并将其加入小根堆。然后,每次从堆中取出距离最小的节点,遍历其邻居节点,如果到达邻居节点的路径比已知的最短路径更短,则更新邻居节点的距离和父节点,并将其加入堆中。在实现中,我们使用了 distances 和 parents 两个向量来分别存储最短路径和父节点,使用了 minHeap 来存储节点和距离,其中我们使用了 std::greater<> 来定义小根堆。最后,我们返回距离向量,并在 main 函数中输出结果。
三、java 最短路径 源码实现及详解
Java实现最短路径的常用算法有很多,如Dijkstra算法、Bellman-Ford算法、Floyd算法等。下面以Dijkstra算法为例,介绍一下它的源码实现及详解。
Dijkstra算法是一种贪心算法,用于求带权有向图中一个顶点到其它顶点的最短路径。具体思想是:从源点开始,每次选择距离它最近的一个未标记顶点,标记它并更新从源点到它的距离。重复该操作直到所有顶点都被标记为止。
下面是Dijkstra算法的Java实现代码:
import java.util.Arrays;
import java.util.PriorityQueue;
public class Dijkstra {
private int[] dist; // 距离
private boolean[] visited; // 是否访问
private int[][] graph; // 图
public int[] dijkstra(int[][] graph, int start) {
this.graph = graph;
int n = graph.length;
dist = new int[n];
visited = new boolean[n];
Arrays.fill(dist, Integer.MAX_VALUE);
dist[start] = 0;
PriorityQueue<Integer> minHeap = new PriorityQueue<>((a, b) -> dist[a] - dist[b]);
minHeap.offer(start);
while (!minHeap.isEmpty()) {
int u = minHeap.poll();
visited[u] = true;
for (int v = 0; v < n; v++) {
if (graph[u][v] != 0 && !visited[v]) {
int newDist = dist[u] + graph[u][v];
if (newDist < dist[v]) {
dist[v] = newDist;
minHeap.offer(v);
}
}
}
}
return dist;
}
}
该算法的时间复杂度为O(nlogn),其中n是顶点数。具体实现过程如下:
- 初始化dist数组,将起点的距离dist[start]设为0,其它顶点的距离设为无穷大。
- 将起点start加入最小堆中。
- 重复以下操作,直到最小堆为空:
- 从最小堆中取出距离起点最近的顶点u。
- 标记该顶点为已访问。
- 遍历u的所有邻居节点v,如果v未被访问过,那么计算从起点start到v的新距离newDist,如果newDist小于dist[v],则更新dist[v]的值为newDist,将v加入最小堆中。
最终得到的dist数组即为起点到各个顶点的最短路径。























 135
135











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








