凸函数笔记（2）

4. 凸函数的结构

本节将证明： 给定凸函数 $f$ 的一个相对内点 $x$, 必存在过 $(x,f(x))$ 的一个仿射函数$y=f(x)+v^T(y-x)$ 支撑函数 $f$. 进而说明，下半连续的凸函数是仿射函数的逐点上确界.

函数 $f:{\mathbb{R}}^n\to \overline{\mathbb{R}}$ 称为是下半连续的，是指对 ${\mathbb{R}}^n$ 中任意收敛的点列 $x_k\to x(k\to \infty )$ 有$$f(x)\le \underset{k\to \infty }{\lim }f(x_k).$$下半连续的函数也称为闭函数.

命题 4.1 (切平面的存在性)：设 f : R n → R ∪ { ∞ } f:\mathbb{R}^n\to\mathbb{R}\cup\{\infty\} f:Rn→R∪{∞} 是真凸函数，$x\in \mathbf{ri}(\mathbf{dom}(f))$,则存在 $v\in {\mathbb{R}}^n$ 使得$$\begin{array}{r}f(y)\ge f(x)+v^T(y-x),\forall y\in {\mathbb{R}}^n.\end{array}$$因而 $f$ 在有界集上有下界. 特别，若 $f$ 在 $x$ 处可微，则 $v=\nabla f(x)$

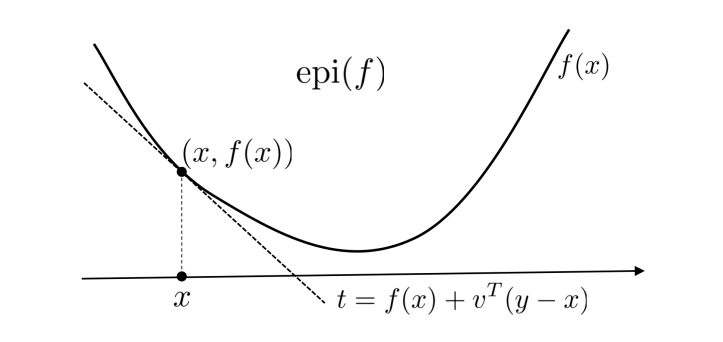
证： 所需证的结论意味着切平面 $t=f(x)+v^T(y-x)$ 是上镜图 $\mathbf{epi}(f)$ 的支撑超平面，如图 4.1所示，由于 $\mathbf{epi}(f)$ 是 ${\mathbb{R}}^{n+1}$ 中一凸集，$(x,f(x))$ 是边界上一点，所以这样的超平面是存在的. 但需要证明该超平面不与 ${\mathbb{R}}^{n+1}$ 中坐标向量 (0,…,0,1) 平行.

图 4.1：支撑超平面示意图

第一步： 支撑超平面的存在性： 设 $x\in \mathbf{ri}(\mathbf{dom}(f))$. 因为 $\mathbf{epi}(f)$是凸集，显然$(x,f(x))\in \mathbf{cl}(\mathbf{epi}(f))\setminus \mathbf{ri}(\mathbf{epi}(f))$.根据支撑超平面命题, 存在 $(a^T,b{)}^T\in {\mathbb{R}}^{n+1}$,使得$$(a^T,b)[\left(\begin{array}{c}y\\ t\end{array}\right)-\left(\begin{array}{c}x\\ f(x)\end{array}\right)]\ge 0,\forall \left(\begin{array}{c}y\\ t\end{array}\right)\in \mathbf{epi}(f),$$其中等号不恒成立.显然上式可化为$$\begin{array}{r}{a}^T(y-x)+b(t-f(x))\ge 0,\forall y\in \mathbf{dom}(f),t\ge f(y),\end{array}$$且存在 $\bar{y}\in \mathbf{dom}(f),\bar{t}\ge f(\bar{y})$, 使得 $a^T(\bar{y}-x)+b(\bar{t}-f(x))>0.$

第二步$:b\ge 0$:在(2)中，令$t\to \infty$ 可知 $b\ge 0.$

第三步$:b>0$:若$b=0$,则$$\begin{array}{r}{a}^T(y-x)\ge 0,\forall y\in \mathbf{dom}(f),\end{array}$$且存在 $\bar{y}\in \mathbf{dom}(f)$,使得 $a^T(\bar{y}-x)>0$. 这意味着凸集 $\mathbf{dom}(f)$ 和 { x } \{x\} {x} 被超平面$a^T(y-x)=0$ 真分离.根据凸集分离定理得： r i ( { x } ) ∩ r i ( d o m ( f ) ) = ∅ \mathbf{ri}(\{x\})\cap\mathbf{ri}(\mathbf{dom}(f))=\emptyset ri({x})∩ri(dom(f))=∅.即$x\notin \mathbf{ri}(\mathbf{dom}(f))$.矛盾.所以 $b>0.$

第四步： 切平面的存在性： 记 $v:=-a/b$,代入(2), 并令 $t=f(y)$,便得到$f(y)\ge f(x)+v^T(y-x),\forall y\in \mathbf{dom}(f)$.当$y\in {\mathbb{R}}^n\setminus \mathbf{dom}(f)$ 时，此不等式显然仍成立.

因 $f(x)>-\infty$.对任意的 $r>0$,当 $y\in B(x,r)$ 时，有$$\begin{array}{r}f(y)\ge f(x)+v^T(y-x)\ge f(x)-\Vert v{\Vert }_2\Vert y-x{\Vert }_2\ge f(x)-r\Vert v{\Vert }_2.\end{array}$$所以 $f$ 在 $B(x,r)$ 上有下界.

最后，当 $f$在$x$ 处可微时容易证明 $v=\nabla f(x)$.

注 1：满足(1)的 $v$ 称为 $f$ 在 $x$ 处的次梯度, 记为 $v\in \partial f(x)$. 命题 3.4.1说明, 当 $f$ 是凸函数且 $x\in \mathbf{ri}(\mathbf{dom}(f))$ 时, $\partial f(x)$ 非空.当 $x\notin \mathbf{ri}(\mathbf{dom}(f))$ 时, 次梯度未必存在.

注2：注 2: 证明的第三步也可以不利用凸集分离定理而直接证明： 因 $x\in \mathbf{ri}(\mathbf{dom}(f))$,对任意的$y\in \mathbf{dom}(f)$,根据线段原理 可知，存在 $\lambda >1$, 使得 $y+\lambda (x-y)\in \mathbf{dom}(f).$ 即$$\begin{array}{r}y+\lambda (x-y)=x-(\lambda -1)(y-x)\in \mathbf{dom}(f).\end{array}$$用 $x-(\lambda -1)(y-x)$ 替换(3)中的 $y$ 便得 $-(\lambda -1)a^T(y-x)\ge 0$,即 $a^T(y-x)\le 0.$ 联立(3)得 $a^T(y-x)=0$.与 $a^T(\bar{y}-x)>0$ 矛盾.所以 $b>0.$

命题 4.2： (凸函数是仿射函数族的逐点上确界) 设 f : R n → R ∪ { ∞ } f:\mathbb{R}^n\to\mathbb{R}\cup\{\infty\} f:Rn→R∪{∞} 是凸函数，且下半连续的，那么对任意的 $x\in {\mathbb{R}}^n$, 存在一列仿射函数 { g k } \{g_k\} {gk​}, 使得$$\begin{array}{r}f(y)\ge g_k(y),\forall y\in {\mathbb{R}}^n,g_k(x)\to f(x)(k\to \infty ).\end{array}$$从而 f ( x ) = sup ⁡ { g ( x ) ∣ g 是仿射函数 ,  满足 : g ( y ) ≤ f ( y ) ,   ∀ y ∈ R n } . \begin{align} f(x)=\sup\{g(x)|g\text{是仿射函数},\text{ 满足}:g(y)\leq f(y),\mathrm{~}\forall y\in\mathbb{R}^n\}.\end{align} f(x)=sup{g(x)∣g是仿射函数, 满足:g(y)≤f(y), ∀y∈Rn}.​​

证：根据命题 4.1, 只需考虑 $x\in {\mathbb{R}}^n\setminus \mathbf{ri}(\mathbf{dom}(f))$ 的情形.不妨设 $\mathbf{dom}$$(f)\ne \varnothing$.否则令 $g_k(y)\equiv k,\forall y\in {\mathbb{R}}^n.$

(a) 若$x\in \mathbf{cl}(\mathbf{dom}(f))\backslash \mathbf{ri}(\mathbf{dom}(f))$, 取$x_0\in \mathbf{ri}(\mathbf{dom}(f))$ 和$x_k:=x+\frac{1}{k}(x_0-x),k\in \mathbb{N}.$ 由线段原理可知 $x_k\in \mathbf{ri}(\mathbf{dom}(f))$,于是，利用命题 4.1可知，存在仿射函数 $g_k(y)=$ $\begin{array}{r}f(x_k)+v_k^T(y-x_k),\end{array}$ 使得$$f(y)\ge g_k(y),\forall y\in {\mathbb{R}}^n.$$
在上式中令 $y=x_0$，得：
$$\begin{array}{r}f(x_0)\ge f(x_k)+v_k^T(x_0-x_k)=f(x_k)+(1-\frac{1}{k})v_k^T(x_0-x)\end{array}$$
从而,当 $k\ge 2$ 时, 有：$v_k^T(x_0-x)\le \frac{k}{k-1}[f(x_0)-f(x_k)]$.于是$$\begin{array}{rl}{g}_k(x)& =f(x_k)+v_k^T(x-x_k)=f(x_k)-\frac{1}{k}{v}_k^T(x_0-x)\\ & \ge f(x_k)-\frac{1}{k-1}[f(x_0)-f(x_k)]\\ & =\frac{k}{k-1}f(x_k)-\frac{1}{k-1}f(x_0).\end{array}$$令$k\to \infty$,取下极限，利用 $f$ 的下半连续性，得 $f(x)\le {\underline{\lim }}_{k\to \infty }f(x_k)\le {\underline{\lim }}_{k\to \infty }{g}_k(x).$

又 $f(x)\ge g_k(x),\forall k\in \mathbb{N}$.故 $f(x)\ge {\overline{\lim }}_{k\to \infty }{g}_k(x)$.所以 ${\lim }_{k\to \infty }{g}_k(x)=f(x).$

(b) 若 $x\in {\mathbb{R}}^n\setminus \mathbf{cl}(\mathbf{dom}(f))$,因 $\mathbf{dom}(f)$ 非空，据 (1)所证，存在仿射函数 $g$,使得$\begin{array}{r}f(y)\ge g(y),\forall y\in {\mathbb{R}}^n.\end{array}$

根据凸集的严格分离命题，存在 $a\in {\mathbb{R}}^n$ 和 $b\in \mathbb{R}$, 使得超平面 $a^{T}x+b=0$ 严格分离$x$ 和 $\mathbf{cl}(\mathbf{dom}(f))$，即

$$a^{T}x+b>0,a^{T}y+b\le 0,\forall y\in \mathbf{cl}(\mathbf{dom}(f)).$$
将$a$ 和 $b$ 乘以适当的正数，可设 (将 $a,b$ 改记为 $a_k,b_k)$
$$a_k^{T}x+b_k=k\text{ 且 }{a}_k^{T}y+b_k\le 0,\forall y\in \mathbf{cl}(\mathbf{dom}(f)).$$令 $g_k(y):=g(y)+a_k^{T}y+b_k$, 则 $g_k$ 仍为仿射函数，满足$$g_k(y)=g(y)+a_k^{T}y+b_k\le g(y)\le f(y),\forall y\in \mathbf{dom}(f),$$且 $g_k(x)=g(x)+k\to \infty ,k\to \infty .$

最后, 利用已证结论容易推出(4)，此部分可以留作练习。

5. 拟凸函数

5.1 定义与等价刻画

凸函数因为其局部极小必为全局极小而在优化理论中具有特别的重要性. 可以将具有这一特性的函数可以推广到更大的函数类, 即拟凸函数.

定义 5.1.1： (拟凸函数) 对函数 $f:{\mathbb{R}}^n\to \overline{\mathbb{R}}$, 如果 f ( θ x + ( 1 − θ ) y ) ≤ max ⁡ { f ( x ) , f ( y ) } , ∀ x , y ∈ d o m ( f ) , θ ∈ [ 0 , 1 ] , \begin{align} f(\theta x+(1-\theta)y)\leq\max\{f(x),f(y)\},\quad\forall x,y\in\mathbf{dom}(f),\quad\theta\in[0,1],\end{align} f(θx+(1−θ)y)≤max{f(x),f(y)},∀x,y∈dom(f),θ∈[0,1],​​则称 $f$ 是拟凸的. 如果上式中的严格不等号对 $x\ne y$ 恒成立，则称 $f$ 是严格拟凸的.

如果 $-f$ 是拟凸 (或严格拟凸) 的, 则称 $f$ 是拟凹 (或严格拟凹) 的. 既是拟凸又是拟凹的函数称为拟线性函数.

拟凸函数的有效定义域 $\mathbf{dom}(f)$ 必为凸集.

易见，拟凸函数的有效定义域 $\mathbf{dom}(f)$必为凸集. 对函数 f : R n → R ∪ { ∞ } f:\mathbb{R}^n\to\mathbb{R}\cup\{\infty\} f:Rn→R∪{∞},易见(5) 等价于 f ( θ x + ( 1 − θ ) y ) ≤ max ⁡ { f ( x ) , f ( y ) } , ∀ x , y ∈ R n , θ ∈ [ 0 , 1 ] . \begin{align} f(\theta x+(1-\theta)y)\leq\max\{f(x),f(y)\},\quad\forall x,y\in\mathbb{R}^n,\quad\theta\in[0,1].\end{align} f(θx+(1−θ)y)≤max{f(x),f(y)},∀x,y∈Rn,θ∈[0,1].​​依据定义容易看出, 凸函数必为拟凸的; 凹函数必为拟凹的. 仿射函数必为拟线性的.

命题 5.1.1 ：(拟凸性的水平集刻画) 函数 f : R n → R ∪ { ∞ } f:\mathbb{R}^n\to\mathbb{R}\cup\{\infty\} f:Rn→R∪{∞}是拟凸的当且仅当: $\forall \alpha \in \mathbb{R}$，水平集 $\mathbf{lev}\alpha (f):=x\in {\mathbb{R}}^n\mid f(x)\le \alpha$ 是凸集.

证：设 $f$ 是拟凸函数，那么，对任意的 $\alpha \in \mathbb{R}$,若 $x,y\in {\mathbf{lev}}_{\alpha }(f)$ 以及 $\forall \theta \in [0,1]$,有
f ( θ x + ( 1 − θ ) y ) ≤ max ⁡ { f ( x ) , f ( y ) } ≤ α . f(\theta x+(1-\theta)y)\leq\max\{f(x),f(y)\}\leq\alpha. f(θx+(1−θ)y)≤max{f(x),f(y)}≤α.
所以 $\theta x+(1-\theta )y\in {\mathbf{lev}}_{\alpha }(f)$.从而 ${\mathbf{lev}}_{\alpha }(f)$ 是凸集.

反之，设对任意的 $\alpha \in \mathbb{R}$, 水平集 ${\mathrm{lev}}_{\alpha }(f)$ 是凸集. 那么，$\forall x,y\in \mathbf{dom}(f)$, 不妨设 $f(y)\le f(x)$,对任意的 $\alpha >f(x)$,有 $x,y\in {\mathbf{lev}}_{\alpha }(f)$. 根据 ${\mathbf{lev}}_{\alpha }(f)$ 凸性可知， $\forall \theta \in [0,1]$,有 $\theta x+(1-\theta )y\in {\mathbf{lev}}_{\alpha }(f)$,从而 $f(\theta x+(1-\theta )y)\le \alpha$.令 $\alpha \to f(x)$,便得 f ( θ x + ( 1 − θ ) y ) ≤ f ( x ) = max ⁡ { f ( x ) , f ( y ) } \begin{aligned}f(\theta x+(1-\theta)y)\leq f(x)=\max\{f(x),f(y)\}\end{aligned} f(θx+(1−θ)y)≤f(x)=max{f(x),f(y)}​.所以 $f$ 是拟凸函数.

定义 5.1.2： (截面函数) 设 $x,y\in \mathbf{dom}(f)$,考虑函数 $f$ 限制在过 $x,y$ 的直线上的函数

$$\begin{array}{r}\varphi (t):=f(x+t(y-x)),t\in \mathbb{R},\end{array}$$它是一个一元函数，称为 $f$ 的截面函数.

命题 5.1.2：(拟凸函数的截面刻画) 函数 $f:{\mathbb{R}}^n\to \overline{\mathbb{R}}$ 是拟凸函数当且仅当如下条件之一成立：

$(\mathrm{5.1.2.1})\forall x,y\in {\mathbb{R}}^n,(7)$所定义的 $\varphi$ 是一元拟凸函数.

$(\mathrm{5.1.2.2})\forall x,y\in {\mathbb{R}}^n,(7)$所定义的 $\varphi$ 满足 ϕ ( t ) ≤ max ⁡ { ϕ ( 0 ) , ϕ ( 1 ) } ,   ∀ t ∈ [ 0 , 1 ] . \phi(t)\leq\max\{\phi(0),\phi(1)\},\:\forall t\in[0,1]. ϕ(t)≤max{ϕ(0),ϕ(1)},∀t∈[0,1].

证：$(a)$设 $f:{\mathbb{R}}^n\to \overline{\mathbb{R}}$ 是拟凸函数，那么 $\forall x,y\in {\mathbb{R}}^n$ 和 $\forall t,s\in \mathbb{R}$ 以及 $\theta \in [0,1]$, 记$\xi :=x+t(y-x),\eta :=x+s(y-x)$.有
$$\theta \xi +(1-\theta )\eta =x+\left(\theta t+(1-\theta )s\right)(y-x).$$于是
ϕ ( θ t + ( 1 − θ ) s ) = f ( θ ξ + ( 1 − θ ) η ) ≤ max ⁡ { f ( ξ ) , f ( η ) } = max ⁡ { ϕ ( t ) , ϕ ( s ) } . \begin{aligned}\phi(\theta t+(1-\theta)s)=f(\theta\xi+(1-\theta)\eta)\leq\max\{f(\xi),f(\eta)\}=\max\{\phi(t),\phi(s)\}.\end{aligned} ϕ(θt+(1−θ)s)=f(θξ+(1−θ)η)≤max{f(ξ),f(η)}=max{ϕ(t),ϕ(s)}.​所以，$\varphi$ 是一个一元拟凸函数. 即 (5.1.2.1) 成立.

$(b)$ 若(5.1.2.1) 成立，那么 $\forall t\in [0,1]$,有 ϕ ( t ) ≤ max ⁡ { ϕ ( 0 ) , ϕ ( 1 ) } \phi(t)\leq\max\{\phi(0),\phi(1)\} ϕ(t)≤max{ϕ(0),ϕ(1)}.故 (5.1.2.2) 成立.

$(c)$ 设(5.1.2.2)成立.那么，$\forall x,y\in {\mathbb{R}}^n$ 及$\theta \in [0,1]$, 有
f ( x + θ ( y − x ) ) = ϕ ( θ ) ≤ max ⁡ { ϕ ( 0 ) , ϕ ( 1 ) } = max ⁡ { f ( x ) , f ( y ) } . f(x+\theta(y-x))=\phi(\theta)\leq\max\{\phi(0),\phi(1)\}=\max\{f(x),f(y)\}. f(x+θ(y−x))=ϕ(θ)≤max{ϕ(0),ϕ(1)}=max{f(x),f(y)}.所以 $f$ 是拟凸函数.

命题 5.1.3：(一元拟凸函数) 函数 $f:\mathbb{R}\to \overline{\mathbb{R}}$ 拟凸当且仅当如下条件成立：

(5.1.3.1) $f$ 在 $\mathbb{R}$ 上单调；

(5.1.3.2) $\mathbb{R}$ 可以被分成互不相交的左右两个区间，使得 $f$ 在左边的区间上递减，在右边的区间上递增.

推论 5.1： 一元函数 $f:\mathbb{R}\to \overline{\mathbb{R}}$ 是拟线性的 (既是拟凸的也是拟凹的) 当且仅当 $f$ 是 $\mathbb{R}$ 上单调函数

5.2 可微函数的拟凸性判定

命题 5.2.1 ：(拟凸性的一阶微分判据) 设函数 f : R n → R ∪ { ∞ } f:\mathbb{R}^n\to\mathbb{R}\cup\{\infty\} f:Rn→R∪{∞} 的有效定义域 $\mathbf{dom}(f)$ 是一个凸集，$f$ 在 $\mathbf{dom}(f)$ 上可微，那么，$f$ 是拟凸函数当且仅当：
$$\begin{array}{r}f(y)\le f(x)\text{蕴含}\nabla f(x{)}^T(y-x)\le 0,\forall x,y\in \mathbf{dom}(f).\end{array}$$

命题 5.2.3 ：(拟凸性的二阶微分判据) 设函数 f : R n → R ∪ { ∞ } f:\mathbb{R}^n\to\mathbb{R}\cup\{\infty\} f:Rn→R∪{∞} 的有效定义域为凸集， $f$ 在 $\mathbf{dom}(f)$ 连续，在 $\mathbf{ri}(\mathbf{dom}(f))$ 上处处二阶连续可微的. 那么，

(5.2.3.1) 当 $f$ 拟凸时，对任意的 $x\in \mathbf{ri}(\mathbf{dom}(f))$ 和 $y\in \mathbf{dom}(f)$,当 $\nabla f(x{)}^T(y-x)=0$时,有 $(y-x{)}^T{\nabla }^{2}f(x)(y-x)\ge 0$;

(5.2.3.2) 若对任意的 $x\in \mathbf{ri}(\mathbf{dom}(f))$ 和 $y\in \mathbf{dom}(f),y\ne x$,当 $\nabla f(x{)}^T(y-x)=0$ 时， 有 $(y-x{)}^T{\nabla }^{2}f(x)(y-x)>0$,则 $f$ 拟凸.

5.3 保拟凸运算

类似于凸函数情形, 可以给出保拟凸运算的若干结果. 这里不加证明地将这些典型的结果罗列在这此.

命题 5.3.1：设 $h:{\mathbb{R}}^m\to \overline{\mathbb{R}}$ 是一个拟凸函数，对 $i=1,\cdots ,m,g_i:C_i\to \mathbb{R}$ 是凸函数或凹函数，其中$C_i\subset {\mathbb{R}}^n$,满足条件：

(5.3.1.1) $g_i$ 是凸函数时，$h$ 关于第 $i$ 个变元 $x_i$ 在 R 上递增； 或

(5.3.1.2) $g_i$ 是凹函数时，$h$ 关于第 $i$ 个变元 $x_i$ 在 R 上递减，

记$$g(x):=(g_1(x),\cdots ,g_m(x){)}^T.$$那么，复合函数$$f=h\circ g,\text{dom}(f):=\{x\in \bigcap _{i=1}^m{C}_i|h(g(x))<\infty \},$$也是拟凸函数.

命题 5.3.2：(关于部分变量的下确界) 设 $g:{\mathbb{R}}^n\times {\mathbb{R}}^m\to \overline{\mathbb{R}}$ 是拟凸函数，$C\subset {\mathbb{R}}^m$ 是非空凸集，那么$$f(x):=\underset{\underset{(x,y)\in \mathbf{dom}(g)}{\inf }}{\inf }g(x,y)$$是拟凸函数.

命题 5.3.3： (逐点上确界) 设 { f γ } γ ∈ Γ , Γ ≠ ∅ \{f_\gamma\}_{\gamma\in\Gamma},\quad\Gamma\neq\emptyset {fγ​}γ∈Γ​,Γ=∅,是 ${\mathbb{R}}^n$ 上一族拟凸函数，则
$$f(x):=\underset{\gamma \in \Gamma }{\sup }{f}_{\gamma }(x)$$也是拟凸函数.

练习

设 g : R n → R ∪ { ∞ } g:\mathbb{R}^n\to\mathbb{R}\cup\{\infty\} g:Rn→R∪{∞} 是一个凸函数， h : R n → R ∪ { − ∞ } h:\mathbb{R}^n\to\mathbb{R}\cup\{-\infty\} h:Rn→R∪{−∞} 是凹函数，在凸集$C\subset {\mathbb{R}}^n$ 上，有 $g(x)\ge 0,h(x)>0$.那么 $f(x):=g(x)/h(x),\mathbf{dom}(f):=C$,是拟凸函数.