矩阵微分笔记（2）

前言

这篇笔记的内容是基于参考的文章写出的，公式部分可以会沿用文章本来的式，但会加入我自己的一些思考以及注释，如果读者认为我写的不够好得话可以参考原文章~

本笔记的内容是学习向量变元的实值标量函数、矩阵变元的实值标量函数中最基础的矩阵求导公式(会对个别重要的公式做证明)。

下面有一个求矩阵导数的网站，可以用来验证求导结果是否正确：Matrix Calculus

基本求导规则

1. 向量变元的实值标量函数

即形如$$f(\vec{x}),\vec{x}=[x_1,x_2,\cdots ,x_n{]}^T$$使用梯度向量形式，则有$${\nabla }_{\vec{x}}f(\vec{x})=\frac{\partial f(\vec{x})}{\partial \vec{x}}={\left[\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\cdots ,\frac{\partial f}{\partial x_n}\right]}^T$$对于该形式的求导法则，与高等数学中的导数的法则的证明思想类似，下面给个4个原则，并选择性给出证明：

1.1 4个法则

（1）：常数求导

与一元函数常数求导相同：结果为零向量，即

$$\frac{\partial c}{\partial \vec{x}}=0_{n\times 1}$$其中，$c$ 为常数

（2）：线性法则

与一元函数求导线性法则相同：相加再求导等于求导再相加，常数提到外面，即：$$\frac{\partial [c_{1}f(\vec{x})+c_{2}g(\vec{x})]}{\partial \vec{x}}=c_1\frac{\partial f(\vec{x})}{\partial \vec{x}}+c_2\frac{\partial g(\vec{x})}{\partial \vec{x}}$$其中，$c_1,c_2$ 为常数。

（3）：乘积法则

与一元函数求导乘积法则相同：前导后不导加前不导后导，即

$$\frac{\partial [f(\vec{x})g(\vec{x})]}{\partial \vec{x}}=\frac{\partial f(\vec{x})}{\partial \vec{x}}g(\vec{x})+f(\vec{x})\frac{\partial g(\vec{x})}{\partial \vec{x}}$$证明：$$\begin{array}{rl}\frac{\partial [f(\vec{x})g(\vec{x})]}{\partial \vec{x}}& =\left[\begin{array}{c}\frac{\partial (fg)}{\partial x_1}\\ \frac{\partial (fg)}{\partial x_2}\\ ⋮\\ \frac{\partial (fg)}{\partial x_n}\end{array}\right]\\ & =\left[\begin{array}{c}\frac{\partial f}{\partial x_1}g+f\frac{\partial g}{\partial x_1}\\ \frac{\partial f}{\partial x_2}g+f\frac{\partial g}{\partial x_2}\\ ⋮\\ \frac{\partial f}{\partial x_n}g+f\frac{\partial g}{\partial x_n}\end{array}\right]\\ & =[\begin{array}{c}\frac{\partial f}{\partial x_1}\\ \frac{\partial f}{\partial x_2}\\ ⋮\\ \frac{\partial f}{\partial x_n}\end{array}]g+f\left[\begin{array}{c}\frac{\partial g}{\partial x_1}\\ \frac{\partial g}{\partial x_2}\\ ⋮\\ \frac{\partial g}{\partial x_n}\end{array}\right]\\ & =\frac{\partial f(\vec{x})}{\partial \vec{x}}g(\vec{x})+f(\vec{x})\frac{\partial g(\vec{x})}{\partial \vec{x}}\end{array}$$

（4）：商法则

与一元函数求导商法则相同：（上导下不导 减 上不导下导）除以（下的平方）：$$\begin{array}{rl}& \frac{\partial \left[\frac{f(\vec{x})}{g(\vec{x})}\right]}{\partial \vec{x}}=\frac{1}{g^2(\vec{x})}\left[\frac{\partial f(\vec{x})}{\partial \vec{x}}g(\vec{x})-f(\vec{x})\frac{\partial g(\vec{x})}{\partial \vec{x}}\right]\end{array}$$其中，$g(\vec{x})\ne 0$

证明：$$\begin{array}{rl}\frac{\partial \left[\frac{f(\vec{x})}{g(\vec{x})}\right]}{\partial \vec{x}}& =[\begin{array}{c}\frac{\partial (\frac{f}{g})}{\partial x_1}\\ \frac{\partial (\frac{f}{g})}{\partial x_2}\\ ⋮\\ \frac{\partial (\frac{f}{g})}{\partial x_n}\end{array}]\\ & =\left[\begin{array}{c}\frac{1}{g^2}\left(\frac{\partial f}{\partial x_1}g-f\frac{\partial g}{\partial x_1}\right)\\ \frac{1}{g^2}\left(\frac{\partial f}{\partial x_2}g-f\frac{\partial g}{\partial x_2}\right)\\ ⋮\\ \frac{1}{g^2}\left(\frac{\partial f}{\partial x_n}g-f\frac{\partial g}{\partial x_n}\right)\end{array}\right]\\ & =\frac{1}{g^2}([\begin{array}{c}\frac{\partial f}{\partial x_1}\\ \frac{\partial f}{\partial x_2}\\ ⋮\\ \frac{\partial f}{\partial x_n}\end{array}]g-f\left[\begin{array}{c}\frac{\partial g}{\partial x_1}\\ \frac{\partial g}{\partial x_2}\\ ⋮\\ \frac{\partial g}{\partial x_n}\end{array}\right])\\ & =\frac{1}{g^2(\vec{x})}\left[\frac{\partial f(\vec{x})}{\partial \vec{x}}g(\vec{x})-f(\vec{x})\frac{\partial g(\vec{x})}{\partial \vec{x}}\right]\end{array}$$如上所述，证明完毕

1.2 常用公式

（1）：
$$\frac{\partial ({\vec{x}}^T\vec{a})}{\partial \vec{x}}=\frac{\partial ({\vec{a}}^T\vec{x})}{\partial \vec{x}}=\vec{a}$$

其中，$\vec{a}$ 为常数向量，即 $\vec{a}=(a_1,a_2,\cdots ,a_n{)}^T$。

证明：该式采用是是向量变元对标量函数的分布布局，结果如下：$$\begin{array}{rl}\frac{\partial ({\vec{x}}^T\vec{a})}{\partial x}& =\frac{\partial ({\vec{a}}^T\vec{x})}{\partial \vec{x}}\\ & =\frac{\partial (a_1{x}_1+a_2{x}_2+\cdots +a_n{x}_n)}{\partial \vec{x}}\\ & =[\begin{array}{c}\frac{\partial (a_1{x}_1+a_2{x}_2+\cdots +a_n{x}_n)}{\partial x_1}\\ \frac{\partial (a_1{x}_1+a_2{x}_2+\cdots +a_n{x}_n)}{\partial x_2}\\ ⋮\\ \frac{\partial (a_1{x}_1+a_2{x}_2+\cdots +a_n{x}_n)}{\partial x_n}\end{array}]\\ & =[\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_n\end{array}]\\ & =\vec{a}\end{array}$$

（2）：$$\frac{\partial ({\vec{x}}^T\vec{x})}{\partial \vec{x}}=2\vec{x}$$证明：该式采用是是向量变元对标量函数的分布布局，结果如下：$$\begin{array}{rl}\frac{\partial ({\vec{x}}^T\vec{x})}{\partial \vec{x}}& =\frac{\partial (x_1^2+x_2^2+\cdots +x_n^2)}{\partial \vec{x}}\\ & =[\begin{array}{c}\frac{\partial (x_1^2+x_2^2+\cdots +x_n^2)}{\partial x_1}\\ \frac{\partial (x_1^2+x_2^2+\cdots +x_n^2)}{\partial x_2}\\ ⋮\\ \frac{\partial (x_1^2+x_2^2+\cdots +x_n^2)}{\partial x_n}\end{array}]\\ & =\left[\begin{array}{c}2x_1\\ 2x_2\\ ⋮\\ 2x_n\end{array}\right]\\ & =2[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}]\\ & =2\vec{x}\end{array}$$

（3）：
$$\frac{\partial ({\vec{x}}^{T}A\vec{x})}{\partial \vec{x}}=A\vec{x}+A^T\vec{x}$$其中，$A_{n\times n}$是常数矩阵，$A_{n\times n}=(a_{ij}{)}_{i=1,j=1}^{n,n}$

证明：$$\begin{gathered} \begin{array}{rl}\frac{\partial ({\vec{x}}^{T}A\vec{x})}{\partial \vec{x}}& =(x_1,x_2,\dots ,x_n)\left(\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right)\\ & =\frac{\partial (a_{11}{x}_1{x}_1+a_{12}{x}_1{x}_2+\cdots +a_{1n}{x}_1{x}_n \\ +a_{21}{x}_2{x}_1+a_{22}{x}_2{x}_2+\cdots +a_{2n}{x}_2{x}_n \\ +\cdots \\ +a_{n1}{x}_n{x}_1+a_{n2}{x}_n{x}_2+\cdots +a_{nn}{x}_n{x}_n)}{\partial \vec{x}}\\ & \\ & =\left[\begin{array}{c}\frac{\partial (a_{11}{x}_1{x}_1+a_{12}{x}_1{x}_2+\cdots +a_{1n}{x}_1{x}_n \\ +a_{21}{x}_2{x}_1+a_{22}{x}_2{x}_2+\cdots +a_{2n}{x}_2{x}_n \\ +\cdots \\ +a_{n1}{x}_n{x}_1+a_{n2}{x}_n{x}_2+\cdots +a_{nn}{x}_n{x}_n)}{\partial x_1}\\ \frac{\partial (a_{11}{x}_1{x}_1+a_{12}{x}_1{x}_2+\cdots +a_{1n}{x}_1{x}_n \\ +a_{21}{x}_2{x}_1+a_{22}{x}_2{x}_2+\cdots +a_{2n}{x}_2{x}_n \\ +\cdots \\ +a_{n1}{x}_n{x}_1+a_{n2}{x}_n{x}_2+\cdots +a_{nn}{x}_n{x}_n)}{\partial x_2}\\ ⋮\\ \frac{\partial (a_{11}{x}_1{x}_1+a_{12}{x}_1{x}_2+\cdots +a_{1n}{x}_1{x}_n \\ +a_{21}{x}_2{x}_1+a_{22}{x}_2{x}_2+\cdots +a_{2n}{x}_2{x}_n \\ +\cdots \\ +a_{n1}{x}_n{x}_1+a_{n2}{x}_n{x}_2+\cdots +a_{nn}{x}_n{x}_n)}{\partial x_n}\end{array}\right]\\ & \\ & =\left[\begin{array}{c}(a_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n)+(a_{11}{x}_1+a_{21}{x}_2+\cdots +a_{n1}{x}_n)\\ (a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n)+(a_{12}{x}_1+a_{22}{x}_2+\cdots +a_{n2}{x}_n)\\ ⋮\\ (a_{n1}{x}_1+a_{n2}{x}_2+\cdots +a_{nn}{x}_n)+(a_{1n}{x}_1+a_{2n}{x}_2+\cdots +a_{nn}{x}_n)\end{array}\right]\\ & \\ & =\left[\begin{array}{c}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n\\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n\\ ⋮\\ a_{n1}{x}_1+a_{n2}{x}_2+\cdots +a_{nn}{x}_n\end{array}\right]+\left[\begin{array}{c}{a}_{11}{x}_1+a_{21}{x}_2+\cdots +a_{n1}{x}_n\\ a_{12}{x}_1+a_{22}{x}_2+\cdots +a_{n2}{x}_n\\ ⋮\\ a_{1n}{x}_1+a_{2n}{x}_2+\cdots +a_{nn}{x}_n\end{array}\right]\\ & \\ & =\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]+\left[\begin{array}{cccc}{a}_{11}& a_{21}& \cdots & a_{n1}\\ a_{12}& a_{22}& \cdots & a_{n2}\\ ⋮& ⋮& \ddots & ⋮\\ a_{1n}& a_{2n}& \cdots & a_{nn}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]\\ & \\ & =A\vec{x}+A^T\vec{x}\end{array} \\ \text{\hspace{1em}(14)} \end{gathered}$$上述的第一个等号是直接按照定义展开得到的，由于分子 ${\vec{x}}^{T}A\vec{x}$ 实际上是一个标量，于是我们可以应用向量对标量函数的导数的求导法则来计算。通过观察我们可以发现结果布局是 $n\times 1$ 维的，且第一个分量的结果可以分成两项：是$A$ 的第一列的转置与 $\vec{x}$ 的内积以及 $A$ 的第一行与 $\vec{x}$ 的内积，为此可以很自然地计算剩余的分量

（4）：$$\frac{\partial ({\vec{a}}^T\vec{x}{\vec{x}}^T\vec{b})}{\partial \vec{x}}=a{b}^T\vec{x}+b{a}^T\vec{x}$$其中$\vec{a},\vec{b}$ 为常数向量，$\vec{a}=(a_1,a_2,\cdots ,a_n{)}^T,\vec{b}=(b_1,b_2,\cdots ,b_n{)}^T$

证明：因为 ${\vec{a}}^T\vec{x}={\vec{x}}^T\vec{a},{\vec{x}}^T\vec{b}={\vec{b}}^T\vec{x}$ ，所以有$$\frac{\partial ({\vec{a}}^T\vec{x}{\vec{x}}^T\vec{b})}{\partial \vec{x}}=\frac{\partial ({\vec{x}}^T\vec{a}{\vec{b}}^T\vec{x})}{\partial \vec{x}}$$因为 $\vec{a}{\vec{b}}^T$ 是常数矩阵，于是可以利用公式 $$\frac{\partial ({\vec{x}}^{T}A\vec{x})}{\partial \vec{x}}=A\vec{x}+A^T\vec{x}$$得到$$\frac{\partial ({\vec{a}}^T\vec{x}{\vec{x}}^T\vec{b})}{\partial \vec{x}}=\frac{\partial ({\vec{x}}^T\vec{a}{\vec{b}}^T\vec{x})}{\partial \vec{x}}=\vec{a}{\vec{b}}^T\vec{x}+\vec{b}{\vec{a}}^T\vec{x}$$如上所述，证明完毕

2. 矩阵变元的实值标量函数

$$f(\mathbf{X}),{\mathbf{X}}_{m\times n}=(x_{ij}{)}_{i=1,j=1}^{m,n}$$利用梯度矩阵的形式，也就是矩阵变元的标量函数里的分母布局的形式，有：$$\begin{array}{rl}{\nabla }_{X}f(\mathbf{X})& =\frac{\partial f(\mathbf{X})}{\partial {\mathbf{X}}_{m\times n}}\\ & ={\left[\begin{array}{cccc}\frac{\partial f}{\partial x_{11}}& \frac{\partial f}{\partial x_{12}}& \cdots & \frac{\partial f}{\partial x_{1n}}\\ \frac{\partial f}{\partial x_{21}}& \frac{\partial f}{\partial x_{22}}& \cdots & \frac{\partial f}{\partial x_{2n}}\\ ⋮& ⋮& ⋮& ⋮\\ \frac{\partial f}{\partial x_{m1}}& \frac{\partial f}{\partial x_{m2}}& \cdots & \frac{\partial f}{\partial x_{mn}}\end{array}\right]}_{m\times n}\end{array}$$类似于向量变元的实值标量函数，给出下面给个4个原则，并选择性给出证明：

2.1 4个法则

我们设讨论的矩阵 $X$ 是 $m\times n$ 维的

（1）：常数求导

与一元函数常数求导相同：结果为零矩阵，即

$$\frac{\partial c}{\partial X}=0_{m\times n}$$其中，$c$ 为常数

（2）：线性法则

与一元函数求导线性法则相同：相加再求导等于求导再相加，常数提到外面，即：$$\frac{\partial [c_{1}f(X)+c_{2}g(X)]}{\partial X}=c_1\frac{\partial f(X)}{\partial X}+c_2\frac{\partial g(X)}{\partial X}$$其中，$c_1,c_2$ 为常数。

（3）：乘积法则

与一元函数求导乘积法则相同：前导后不导加前不导后导，即$$\frac{\partial [f(\mathbf{X})g(\mathbf{X})]}{\partial \mathbf{X}}=\frac{\partial f(\mathbf{X})}{\partial \mathbf{X}}g(\mathbf{X})+f(\mathbf{X})\frac{\partial g(\mathbf{X})}{\partial \mathbf{X}}$$

证明：由于矩阵变元的实值标量函数是对逐一每个元素 $d{x}_{ij}$ 的导数，为此利用向量变元的实值标量函数的乘积法则有：$$\begin{gathered} \begin{array}{rl}\frac{\partial [f(X)g(X)]}{\partial X}& =\left[\begin{array}{cccc}\frac{\partial (fg)}{\partial x_{11}}& \frac{\partial (fg)}{\partial x_{12}}& \cdots & \frac{\partial (fg)}{\partial x_{1n}}\\ \frac{\partial (fg)}{\partial x_{21}}& \frac{\partial (fg)}{\partial x_{22}}& \cdots & \frac{\partial (fg)}{\partial x_{2n}}\\ ⋮& ⋮& ⋮& ⋮\\ \frac{\partial (fg)}{\partial x_{m1}}& \frac{\partial (fg)}{\partial x_{m2}}& \cdots & \frac{\partial (fg)}{\partial x_{mn}}\end{array}\right]\\ & \\ & =\left[\begin{array}{cccc}\frac{\partial f}{\partial x_{11}}g+f\frac{\partial g}{\partial x_{11}}& \frac{\partial f}{\partial x_{12}}g+f\frac{\partial g}{\partial x_{12}}& \cdots & \frac{\partial f}{\partial x_{1n}}g+f\frac{\partial g}{\partial x_{1n}}\\ \frac{\partial f}{\partial x_{21}}g+f\frac{\partial g}{\partial x_{21}}& \frac{\partial f}{\partial x_{22}}g+f\frac{\partial g}{\partial x_{22}}& \cdots & \frac{\partial f}{\partial x_{2n}}g+f\frac{\partial g}{\partial x_{2n}}\\ ⋮& ⋮& ⋮& ⋮\\ \frac{\partial f}{\partial x_{m1}}g+f\frac{\partial g}{\partial x_{m1}}& \frac{\partial f}{\partial x_{m2}}g+f\frac{\partial g}{\partial x_{m2}}& \cdots & \frac{\partial f}{\partial x_{mn}}g+f\frac{\partial g}{\partial x_{mn}}\end{array}\right]\\ & \\ & =\left[\begin{array}{cccc}\frac{\partial f}{\partial x_{11}}& \frac{\partial f}{\partial x_{12}}& \cdots & \frac{\partial f}{\partial x_{1n}}\\ \frac{\partial f}{\partial x_{21}}& \frac{\partial f}{\partial x_{22}}& \cdots & \frac{\partial f}{\partial x_{2n}}\\ ⋮& ⋮& ⋮& ⋮\\ \frac{\partial f}{\partial x_{m1}}& \frac{\partial f}{\partial x_{m2}}& \cdots & \frac{\partial f}{\partial x_{mn}}\end{array}\right]g+f\left[\begin{array}{cccc}\frac{\partial g}{\partial x_{11}}& \frac{\partial g}{\partial x_{12}}& \cdots & \frac{\partial g}{\partial x_{1n}}\\ \frac{\partial g}{\partial x_{21}}& \frac{\partial g}{\partial x_{22}}& \cdots & \frac{\partial g}{\partial x_{2n}}\\ ⋮& ⋮& ⋮& ⋮\\ \frac{\partial g}{\partial x_{m1}}& \frac{\partial g}{\partial x_{m2}}& \cdots & \frac{\partial g}{\partial x_{mn}}\end{array}\right]\\ & \\ & =\frac{\partial f(X)}{\partial X}g(X)+f(X)\frac{\partial g(X)}{\partial X}\end{array} \\ \text{\hspace{1em}(23)} \end{gathered}$$即证

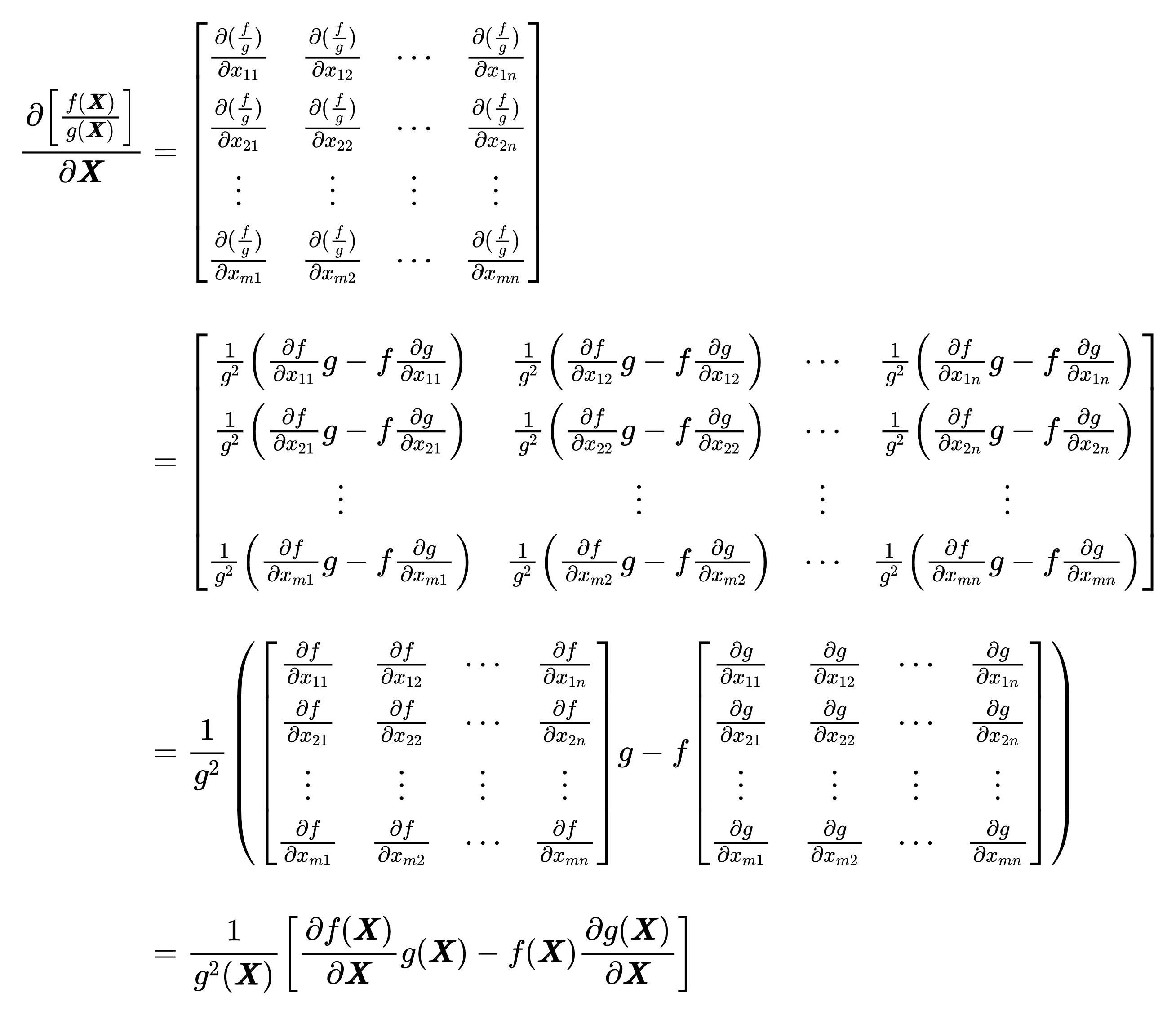
（4）：商法则

与一元函数求导商法则相同：（上导下不导 减 上不导下导）除以（下的平方）：$$\begin{array}{rl}& \frac{\partial \left[\frac{f(\mathbf{X})}{g(\mathbf{X})}\right]}{\partial \mathbf{X}}=\frac{1}{g^2(\mathbf{X})}[\frac{\partial f(\mathbf{X})}{\partial \mathbf{X}}g(\mathbf{X})-f(\mathbf{X})\frac{\partial g(\mathbf{X})}{\partial \mathbf{X}}]\end{array}$$其中，$g(\mathbf{X})\ne 0$.

证明（由于Latex太长了放不下，就用图片吧）：

2.2 常用公式

（1）：

$$\frac{\partial ({\vec{a}}^T\mathbf{X}\vec{b})}{\partial \mathbf{X}}=\vec{a}{\vec{b}}^T$$

其中，${\vec{a}}_{m\times 1},{\vec{b}}_{n\times 1}$ 为常数向量，${\vec{a}}_{=}(a_1,a_2,\cdots ,a_m{)}^T,\vec{b}=(b_1,b_2,\cdots ,b_n{)}^T$

证明（同样因为Latex公式太长了，就不放了）

（2）：

$$\frac{\partial ({\vec{a}}^T{\mathbf{X}}^T\vec{b})}{\partial \mathbf{X}}=\vec{b}{\vec{a}}^T$$其中${\vec{a}}_{=}(a_1,a_2,\cdots ,a_n{)}^T,\vec{b}=(b_1,b_2,\cdots ,b_m{)}^T$

证明：我们发现分子实际上是一个标量，因为标量的转置等于标量自己，所以有
$$\frac{\partial ({\vec{a}}^T{\mathbf{X}}^T\vec{b})}{\partial \mathbf{X}}=\frac{\partial ({\vec{a}}^T{\mathbf{X}}^T\vec{b}{)}^T}{\partial \mathbf{X}}=\frac{\partial ({\vec{b}}^T\mathbf{X}\vec{a})}{\partial \mathbf{X}}$$由上述已经证明的公式$$\frac{\partial ({\vec{a}}^T\mathbf{X}\vec{b})}{\partial \mathbf{X}}=\vec{a}{\vec{b}}^T$$可以得到$$\frac{\partial ({\vec{a}}^T{\mathbf{X}}^T\vec{b})}{\partial \mathbf{X}}=\frac{\partial ({\vec{a}}^T{\mathbf{X}}^T\vec{b}{)}^T}{\partial \mathbf{X}}=\frac{\partial ({\vec{b}}^T\mathbf{X}\vec{a})}{\partial \mathbf{X}}=\vec{b}{\vec{a}}^T$$

（3）：

$$\frac{\partial ({\vec{a}}^T\mathbf{X}{\mathbf{X}}^T\vec{b})}{\partial \mathbf{X}}=\vec{a}{\vec{b}}^T\mathbf{X}+\vec{b}{\vec{a}}^T\mathbf{X}$$

其中，${\vec{a}}_{m\times 1},{\vec{b}}_{m\times 1}$ 为常数向量，${\vec{a}}_{=}(a_1,a_2,\cdots ,a_m{)}^T,\vec{b}=(b_1,b_2,\cdots ,b_m{)}^T$

由于证明比较长，就不给出了，感兴趣的读者可以去参考中参考原作者的证明。证明过程实际是按照矩阵变元对实值标量函数的求定义，对每一个元素求导后证明的，过程比较复杂，当然了后面会有更为简洁的办法。

（4）：

$$\frac{\partial ({\vec{a}}^T{\mathbf{X}}^T\mathbf{X}\vec{b})}{\partial \mathbf{X}}=\mathbf{X}\vec{a}{\vec{b}}^T+\mathbf{X}\vec{b}{\vec{a}}^T$$

本次笔记到这里就结束了，由于我只是对原内容的学习，当然不会写的太过详细，因此感兴趣的读者可以去读原文哦（再三强调~）

写到这不免会觉得后面那几个求导公式按照定义推导非常麻烦，而且过程也不易懂，好在如果利用矩阵的迹与一阶实矩阵微分 $dX$ 就可以简洁地证明上述的公式，为此让我们在下一篇博文中看看是如何做的吧（特别安利~）

参考

矩阵求导公式的数学推导（矩阵求导——基础篇）

张贤达《矩阵分析与应用（第二版）》